Урок по теме "Свойства поверхности жидкости. Капиллярные явления". Капиллярные свойства воды

Капиллярные явления (физика). Капиллярные явления в природе :: SYL.ru

Среди процессов, которые можно объяснить с помощью поверхностного натяжения и смачивания жидкостей, стоит особо выделить капиллярные явления. Физика – это загадочная и необыкновенная наука, без которой жизнь на Земле была бы невозможна. Давайте рассмотрим наиболее яркий пример этой важной дисциплины.

В жизненной практике такие интересные с точки зрения физики процессы, как капиллярные явления, встречаются весьма часто. Все дело в том, что в повседневной жизни нас окружает много тел, которые легко впитывают в себя жидкость. Причина этому – их пористая структура и элементарные законы физики, а результат – капиллярные явления.

Узкие трубки

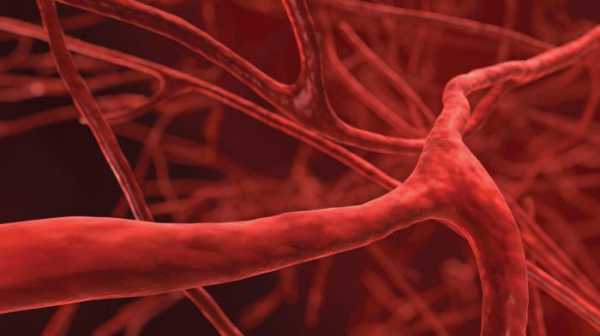
Капилляр – это очень узкая трубка, в которой жидкость ведет себя особым образом. Примеров таких сосудов много в природе – капилляры кровеносной системы, пористых тел, почвы, растений и т. д.

Капиллярным явлением называется подъем или опускание жидкостей по узким трубкам. Такие процессы наблюдаются в естественных каналах человека, растений и других тел, а также в специальных узких сосудах из стекла. На картинке видно, что в сообщающихся трубках разной толщины установился разный уровень воды. Отмечено, что чем тоньше сосуд, тем выше уровень воды.

Эти явления лежат в основе впитывающих свойств полотенца, питания растений, движения чернил по стержню и многих других процессов.

Капиллярные явления в природе

Описанный выше процесс чрезвычайно важен для поддержания жизнедеятельности растений. Почва довольно рыхлая, между ее частицами существуют промежутки, которые представляют собой капиллярную сеть. По этим каналам поднимается вода, питая корневую систему растений влагой и всеми необходимыми веществами.

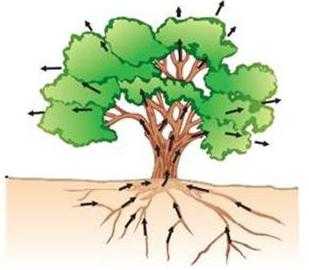
По этим же капиллярам жидкость активно испаряется, поэтому необходимо производить вспахивание земли, которое разрушит каналы и удержит питательные вещества. И наоборот, прижатая земля быстрее испарит влагу. Этим обусловлена важность перепашки земли для удержания подпочвенной жидкости.

В растениях капиллярная система обеспечивает подъем влаги от мелких корешков до самых верхних частей, а через листья она испаряется во внешнюю среду.

Поверхностное натяжение и смачивание

В основе вопроса о поведении жидкости в сосудах лежат такие физические процессы, как поверхностное натяжение и смачивание. Капиллярные явления, обусловленные ими, изучаются в комплексе.

Под действием силы поверхностного натяжения смачивающая жидкость в капиллярах находится выше уровня, на котором она должна находиться согласно закону сообщающихся сосудов. И наоборот, несмачивающая субстанция располагается ниже этого уровня.

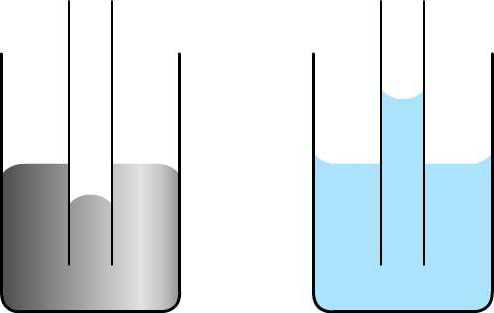
Так, вода в стеклянной трубке (смачивающая жидкость) поднимается на тем большую высоту, чем тоньше сосуд. Напротив, ртуть в стеклянной пробирке (несмачивающая жидкость) опускается тем ниже, чем тоньше эта емкость. Кроме того, как указано на картинке, смачивающая жидкость образует вогнутую форму мениска, а несмачивающая – выпуклую.

Смачивание

Это явление, которое происходит на границе, где жидкость соприкасается с твердым телом (другой жидкостью, газами). Оно возникает по причине особого взаимодействия молекул на границе их контакта.

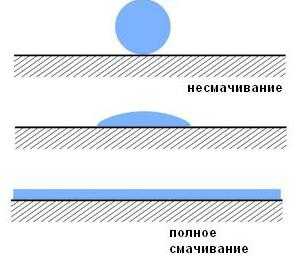
Полное смачивание означает, что капля растекается по поверхности твердого тела, а несмачивание преобразует ее в сферу. На практике чаще всего встречается та или иная степень смачивания, нежели крайние варианты.

Сила поверхностного натяжения

Поверхность капли имеет шарообразную форму и причина этому закон, действующий на жидкости, – поверхностное натяжение.

Капиллярные явления связаны с тем, что вогнутая сторона жидкости в трубке стремится выпрямиться до плоского состояния благодаря силам поверхностного натяжения. Это сопровождается тем, что наружные частицы увлекают за собой вверх тела, находящиеся под ними, и субстанция поднимается вверх по трубке. Однако жидкость в капилляре не может принимать плоскую форму поверхности, и этот процесс подъема продолжается до определенного момента равновесия. Чтобы рассчитать высоту, на которую поднимется (опустится) столб воды, нужно воспользоваться формулами, которые будут представлены ниже.

Расчет высоты подъема столба воды

Момент остановки подъема воды в узкой трубке наступает, когда сила тяжести Ртяж субстанции уравновесит силу поверхностного натяжения F. Этот момент определяет высоту подъема жидкости. Капиллярные явления обусловлены двумя разнонаправленными силами:

сила тяжести Ртяж заставляет жидкость опускаться вниз;
сила поверхностного натяжения F двигает воду вверх.

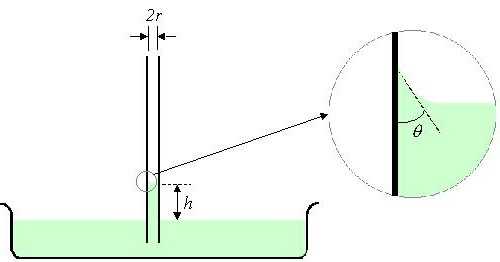
Сила поверхностного натяжения, действующая по окружности, где жидкость соприкасается со стенками трубки, равна:

F = σ2πr,

где r – радиус трубки.

Сила тяжести, действующая на жидкость в трубке равна:

Ртяж = ρπr2hg,

где ρ – плотность жидкости; h – высота столба жидкости в трубке;

Итак, субстанция прекратит подниматься при условии, что Ртяж = F, а это значит, что

ρπr2hg = σ2πr,

отсюда высота жидкости в трубке равна:

h=2σ/pqr.

Точно так же для несмачивающей жидкости:

h – это высота опускания субстанции в трубке. Как видно из формул, высота, на которую поднимется вода в узком сосуде (опустится) обратно пропорционально радиусу емкости и плотности жидкости. Это касается смачивающей жидкости и несмачивающей. При других условиях нужно делать поправку по форме мениска, что будет представлено в следующей главе.

Лапласовское давление

Как уже отмечалось, жидкость в узких трубках ведет себя так, что создается впечатление нарушения закона сообщающихся сосудов. Этот факт всегда сопровождает капиллярные явления. Физика объясняет это с помощью лапласовского давления, которое при смачивающей жидкости направлено вверх. Опуская очень узкую трубку в воду, наблюдаем, как жидкость втягивается на определенный уровень h. По закону сообщающихся сосудов, она должна была уравновеситься с внешним уровнем воды.

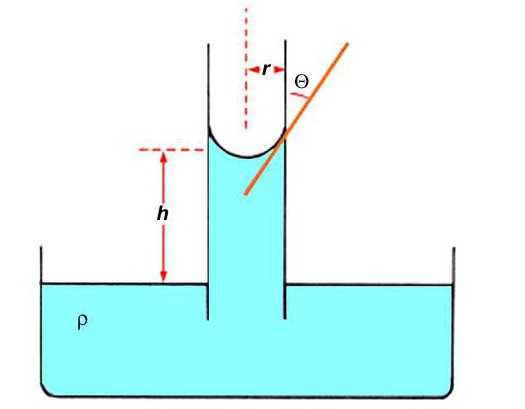
Это несоответствие объясняется направлением лапласовского давления pл:

pл=2σ/R,

В данном случае оно направлено вверх. Вода втягивается в трубку до уровня, где приходит уравновешивание с гидростатическим давлением pг столба воды:

pг=pqh,

а если pл=pг, то можно приравнять и две части уравнения:

2σ/R= pqh.

Теперь высоту h легко вывести в виде формулы:

h=2σ/pqR.

Когда смачивание полное, тогда мениск, который образует вогнутая поверхность воды, имеет форму полусферы, где Ɵ=0. В таком случае радиус сферы R будет равен внутреннему радиусу капилляра r. Отсюда получаем:

h=2σ/pqr.

А в случае неполного смачивания, когда Ɵ≠0, радиус сферы можно вычислить по формуле:

R=r/cosƟ.

Тогда искомая высота, имеющая поправку на угол, будет равна:

h=(2σ/pqr)cos Ɵ.

Из представленных уравнений видно, что высота h обратно пропорциональна внутреннему радиусу трубки r. Наибольшей высоты вода достигает в сосудах, имеющих диаметр человеческого волоса, которые и называются капиллярами. Как известно, смачивающая жидкость втягивается вверх, а несмачивающая – выталкивается вниз.

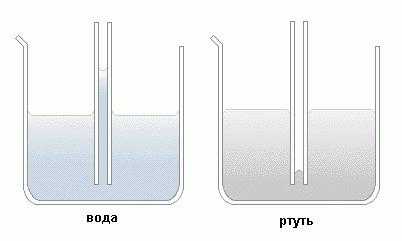
Можно провести эксперимент, взяв сообщающиеся сосуды, где один из них широкий, а другой – очень узкий. Налив туда воду, можно отметить разный уровень жидкости, причем в варианте со смачивающей субстанцией уровень в узкой трубке выше, а с несмачивающей – ниже.

Важность капиллярных явлений

Без капиллярных явлений существование живых организмов просто невозможно. Именно по мельчайшим сосудам человеческое тело получает кислород и питательные вещества. Корни растений – это сеть капилляров, которая вытягивает влагу из земли, донося ее до самых верхних листьев.

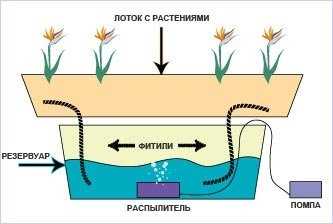
Простая бытовая уборка невозможна без капиллярных явлений, ведь по этому принципу ткань впитывает воду. Полотенце, чернила, фитиль в масляной лампе и множество устройств работает на этой основе. Капиллярные явления в технике играют важную роль при сушке пористых тел и других процессах.

Порой эти же явления дают нежелательные последствия, например, поры кирпича впитывают влагу. Чтобы избежать отсыревания зданий под воздействием грунтовых вод, нужно защитить фундамент с помощью гидроизолирующих материалов – битума, рубероида или толя.

Промокание одежды во время дождя, к примеру, брюк до самых колен от ходьбы по лужам также обязано капиллярным явлениям. Вокруг нас множество примеров этого природного феномена.

Эксперимент с цветами

Примеры капиллярных явлений можно найти в природе, особенно если говорить о растениях. Их стволы имеют внутри множество мелких сосудов. Можно провести эксперимент с окрашиванием цветка в какой-либо яркий цвет в результате капиллярных явлений.

Нужно взять ярко окрашенную воду и белый цветок (или лист пекинской капусты, стебель сельдерея) и поставить в стакан с этой жидкостью. Через какое-то время на листьях пекинской капусты можно наблюдать, как краска продвигается вверх. Цвет растения постепенно изменится соответственно краске, в которую он помещен. Это обусловлено движением субстанции вверх по стеблям согласно тем законам, которые были рассмотрены нами в этой статье.

www.syl.ru

Поверхностное натяжение. Капиллярные явления. - О'Пять пО физике!

Поверхностный слой жидкости обладает особыми свойствами. Молекулы жидкости в этом слое находятся в непосредственной близости от другой фазы – газа. Молекула, расположенная вблизи границы раздела жидкость – газ, имеет ближайших соседей только с одной стороны, поэтому сложение всех сил, действующих на эту молекулу, дает равнодействующую, направленную внутрь жидкости. Следовательно, любая молекула жидкости, находящаяся вблизи свободной поверхности, имеет избыток потенциальной энергии, по сравнению с молекулами, находящимися внутри.

Для того чтобы перевести молекулу из объема жидкости на поверхность, необходимо совершить работу. При увеличении поверхности определенного объема жидкости внутренняя энергия жидкости увеличивается. Эта составляющая внутренней энергии пропорциональна площади поверхности жидкости и называется поверхностной энергией. Величина поверхностной энергии зависит от сил молекулярного взаимодействия и количества ближайших соседних молекул. Для различных веществ поверхностная энергия принимает разные значения. Энергия поверхностного слоя жидкости пропорциональна его площади: Е= σ ·Ѕ

Величина силы F, действующей на единицу длины границы поверхности, определяет поверхностное натяжение жидкости: σ =F/L; σ- коэффициент поверхностного натяжения жидкости, Н/м.

Проще всего уловить характер сил поверхностного натяжения, наблюдая образование капли у неплотно закрытого крана. Всмотритесь внимательно, как постепенно растет капля, образуется сужение - шейка и капля отрывается. Поверхностный слой воды ведет себя, как растянутая эластичная пленка.

Можно осторожно положить швейную иглу на поверхность воды. Поверхностная пленка прогнется и не даст игле утонуть.

По этой же причине легкие насекомые – водомерки могут быстро скользить по поверхности воды. Прогиб пленки не позволяет выливаться воде, осторожно налитой в достаточно частое решето.Ткань – это то же решето, образованное переплетением нитей. Поверхностное натяжение сильно затрудняет просачивание воды сквозь нее, и поэтому ткань не промокает мгновенно. Благодаря силам поверхностного натяжения происходит образование пены.

Изменение поверхностного натяжения

При соприкосновении жидкости с твердым телом наблюдается явление смачивания или несмачивания. Если силы взаимодействия между молекулами жидкости и твердого тела больше, чем между молекулами жидкости, то жидкость растекается по поверхности твердого тела, т.е. смачивает и наоборот, если силы взаимодействия между молекулами жидкости больше, чем между молекулами жидкости и твердого тела, то жидкость собирается в каплю и не смачивает поверхность жидкости.

Капиллярные явления.

В природе часто встречаются тела, имеющие пористое строение (пронизаны множеством мелких каналов). Такую структуру имеют бумага, кожа, дерево, почва, многие строительные материалы. Вода или другая жидкость, попадая на такое твердое тело, может впитываться в него, поднимаясь вверх на большую высоту. Так поднимается влага в стеблях растений, керосин поднимается по фитилю, ткань впитывает влагу. Такие явления называются капиллярными.

В узкой цилиндрической трубке смачивающая жидкость за счет сил молекулярного взаимодействия поднимается вверх, принимая вогнутую форму. Под вогнутой поверхностью появляется дополнительное давление, направленное вверх, в связи с чем уровень жидкости в капилляре выше уровня свободной поверхности. Несмачивающая же жидкость принимает выпуклую поверхность. Под выпуклой поверхностью жидкости возникает обратное дополнительное давление, направленное вниз, так что уровень жидкости с выпуклым мениском ниже, чем уровень свободной поверхности.

Величина добавочного давления равна p= 2 σ / R

Жидкость в капилляре поднимается на такую высоту, чтобы давление столба жидкости уравновесило избыточное давление. Высота подъема жидкости в капилляре равна: h = 2 σ / ρgr

Явление смачивания применяют при обогащении руд. Суть обогащения состоит в отделении пустой породы от полезных ископаемых. Этот способ носит название флотации (флотация – всплывание). Раздробленную в мелкий порошок руду взбалтывают в воде, в которую добавлено небольшое количество жидкости, смачивающей полезную руду, например масло. Вдувая в эту смесь воздух, можно отделить обе составляющие. Покрытые пленкой кусочки полезной руды, прилипая к пузырькам воздуха, поднимутся вверх, а порода осядет на дно.

Адсорбция - явление аналогичное смачиванию, наблюдается при соприкосновении твердой и газообразной фаз. Если силы взаимодействия между молекулами твердого тела и газа велики, то тело покрывается слоем молекул газа. Большой адсорбционной способностью обладают пористые вещества. Свойство активированного угля адсорбировать большое количество газа используют в противогазах, в химической промышленности, в медицине.

Значение поверхностного натяжения

Понятие поверхностного натяжения впервые ввел Я. Сегнер (1752). В 1-й половине 19 в. на основе представления о поверхностном натяжении была развита математическая теория капиллярных явлений (П. Лаплас, С. Пуассон, К. Гаусс, А.Ю. Давидов). Во 2-й половине 19 в. Дж. Гиббс развил термодинамическую теорию поверхностных явлений, в которой решающую роль играет поверхностное натяжение. Среди современных актуальных проблем - развитие молекулярной теории поверхностного натяжения различных жидкостей, включая расплавленные металлы. Силы поверхностного натяжения играют существенную роль в явлениях природы, биологии, медицине, в различных современных технологиях, полиграфии, технике, в физиологии нашего организма. Без этих сил мы не могли бы писать чернилами. Обычная ручка не зачерпнула бы чернил из чернильницы, а автоматическая сразу же поставила бы большую кляксу, опорожнив весь свой резервуар. Нельзя было бы намылить руки: пена не образовалась бы. Нарушился бы водный режим почвы, что оказалось бы гибельным для растений. Пострадали бы важные функции нашего организма. Проявления сил поверхностного натяжения столь многообразны, что даже перечислить их все нет возможности.

В медицине измеряют динамическое и равновесное поверхностное натяжение сыворотки венозной крови, по которым можно диагностировать заболевание и вести контроль над проводимым лечением. Установлено, что вода с низким поверхностным натяжением биологически более доступна. Она легче вступает в молекулярные взаимодействия, тогда клеткам не надо будет тратить энергию на преодоление поверхностного натяжения.

Непрерывно растут объёмы печати на полимерных плёнках благодаря бурному развитию упаковочной индустрии, высокому спросу на потребительские товары в красочной полимерной упаковке. Важное условие грамотного внедрения подобных технологий — точное определение условий их применения в полиграфических процессах. В полиграфии обработка пластика перед печатью необходима для того, чтобы краска ложилась на материал. Причина заключается в поверхностном натяжении материала. Результат определяется тем, как жидкость смачивает поверхность изделия. Смачивание считается оптимальным, когда капля жидкости остается там же, где она была нанесена. В других случаях жидкость может скатываться в каплю, либо, наоборот, растекаться. Оба случая в равной степени приводят к отрицательным результатам во время переноса краски.

Некоторые выводы:

1. Жидкость может смачивать и не смачивать твёрдое тело. 2. Коэффициент поверхностного натяжения зависит от рода жидкости. 3. Коэффициент поверхностного натяжения зависит от температуры .T ↑σ ↓ 4. Высота подъёма жидкости в капилляре зависит от его диаметра. d ↑ h ↓ 5. Сила поверхностного натяжения зависит от длины свободной поверхности жидкости. l ↑ F ↑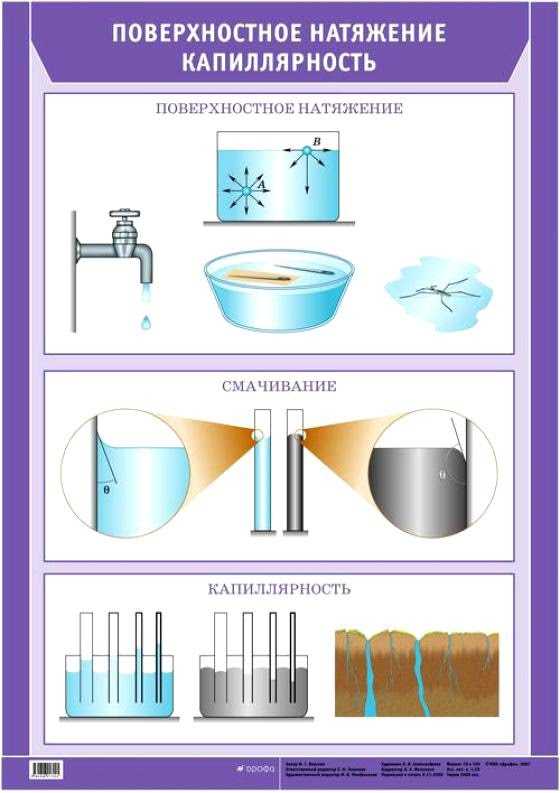

sites.google.com

Явления смачивания. Капиллярные явления

Явления смачивания

На границе раздела жидкости с твердым телом возникают явления смачивания или несмачивания, обусловленные взаимодействием молекул жидкости с молекулами твердого тела:

Если силы притяжения между молекулами жидкости и твердого тела больше сил притяжения между молекулами жидкости . то жидкость будет растекаться по поверхности твердого тела(рис.1, а). Это явление называют смачиванием.
Если сила притяжения между молекулами жидкости и твердого тела меньше сил притяжения между молекулами жидкости , то жидкость не будет растекаться по поверхности твердого тела, а будет собираться в каплю, стремясь уменьшить свою свободную поверхность (рис.1, б). Такое явление называют несмачиванием.

Рис.1 Явления смачивания (а) и несмачивания (б) жидкостью поверхности твердого тела (— краевой угол)

Так как явления смачивания и несмачивания определяются относительными свойствами веществ жидкости и твердого тела, одна и та же жидкость может быть смачивающей для одного твердого тела и несмачивающей для другого. Например, вода смачивает стекло и не смачивает парафин.

Количественной мерой смачивания является краевой угол угол, образуемый поверхностью твердого тела и касательной, проведенной к поверхности жидкости в точке соприкосновения (жидкость находится внутри угла).

При смачивании и чем меньше угол тем сильнее смачивание. Если краевой угол равен нулю, смачивание называют полным или идеальным. К случаю идеального смачивания можно приближенно отнести растекание спирта по чистой поверхности стекла. В этом случае жидкость растекается по поверхности твердого тела до тех пор, пока не покроет всю поверхность.

При несмачивании и чем угол , тем сильнее несмачивание. При значении краевого угла наблюдается полное несмачивание. В этом случае жидкость не прилипает к поверхности твердого тела и легко скатывается с нее. Подобное явление можно наблюдать, когда мы пытаемся вымыть жирную поверхность холодной водой. Моющие свойства мыла и синтетических порошков объясняются тем, что мыльный раствор имеет меньшее поверхностное натяжение, чем вода. Большое поверхностное натяжение воды мешает ей проникать в мелкие поры и промежутки между волокнами ткани.

Явления смачивания и несмачивания играют важную роль в жизни человека. При таких производственных процессах, как склеивание, покраска, пайка очень важно обеспечить смачивание поверхностей. В то время, как обеспечение несмачивания очень важно при создании гидроизоляции, синтезе непромокаемых материалов. В медицине явления смачивания важны для обеспечения движения крови по капиллярам, дыхания и других биологических процессов.

Явления смачивания и несмачивания ярко проявляются в узких трубках – капиллярах.

Капиллярные явления

Смачивающая жидкость поднимается по капилляру. Жидкость, не смачивающая стенки сосуда, опускается в капилляре.

Высота h поднятия жидкости по капилляру определяется соотношением:

где коэффициент поверхностного натяжения жидкости; плотность жидкости; радиус капилляра, ускорение свободного падения.

Глубина , на которую опускается жидкость в капилляре, вычисляется по той же формуле.

Под вогнутым мениском смачивающей жидкости давление меньше, чем под плоской поверхностью. Поэтому жидкость в капилляре поднимается до тех пор. пока гидростатическое давление поднятой в капилляре жидкости на уровне плоской поверхности не скомпенсирует разность давлений. Под выпуклым мениском несмачивающей жидкости давление больше, чем под плоской поверхностью, это приводит к опусканию жидкости в капилляре.

Капиллярные явления мы можем наблюдать и в природе, и в быту. Например, почва имеет рыхлое строение и между ее отдельными частицами находятся промежутки, представляющие собой капилляры. При поливе по капиллярам вода поднимается к корневой системе растений, снабжая их влагой. Также находящаяся в почве вода, поднимаясь по капиллярам. испаряется. Чтобы уменьшить эффективность испарения, тем самым сократив потери влаги, почву разрыхляют, разрушая капилляры. В быту капиллярные явления используются при промокании влажной поверхности бумажным полотенцем или салфеткой.

Примеры решения задач

ru.solverbook.com

Урок по теме "Свойства поверхности жидкости. Капиллярные явления"

Разделы: Физика, Конкурс «Презентация к уроку»

Презентация к уроку

Загрузить презентацию (1,8 МБ)

Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.

Цели:

Познавательная:

познакомить учащихся со свойствами поверхностного слоя жидкости;
сформировать понятие о коэффициенте поверхностного натяжения;
познакомить учащихся с капиллярными явлениями;
совершенствовать навыки учащихся проводить эксперименты;
наблюдать явления и делать выводы.

Воспитательная:

воспитывать умение логически мыслить;
прислушиваться к мнению одноклассников;
умение работать в коллективе.

Развивающая:

развитие познавательного интереса.

Оборудование: компьютер, медиапроектор.

Наглядность: презентация.

Ход урока

Вступительное слово учителя: ребята, сегодня мы с вами продолжим знакомиться со свойствами жидкостей. Мы рассмотрим свойства поверхностного слоя жидкостей и капиллярные явления. Работать будем группами по 4 человека. Вы получите задания, в ходе выполнениях которых, познакомитесь с новыми явлениями, выполните эксперименты, сделаете выводы.

Разминка.

Учитель: Прежде чем начать работу проведем разминку (проводится фронтальный опрос):

Как называется процесс перехода из газообразного состояния вещества в жидкое?
Какое название носит обратный процесс?
От каких факторов зависит скорость испарения жидкости?
Какой пар называют насыщенным?
Почему давление насыщенного пара не зависит от объема?
Какой пар называется ненасыщенным?
Какую температуру называют критической?
Какой процесс называется кипением.
Почему температура остается постоянной в процессе кипения?
Как температура кипения зависит от давления воздуха над жидкостью?

Учащиеся отвечают на вопросы, учитель подтверждает правильные ответы, демонстрируя презентацию. Слайды 4-13

Учитель: Молодцы! Переходим к следующему этапу нашей работы. Перечислите известные вам свойства жидкостей. Как можно объяснить эти свойства с точки зрения молекулярного строения жидкости?

Ученики: Жидкости состоят из молекул, расстояния между которыми сравнимы с размерами самих молекул. Молекулы колеблются относительно положений равновесия и перескакивают с одного места на другое, время "оседлой жизни" составляет примерно 10-8 с. Жидкости текучи, практически несжимаемы. Они сохраняю объем, но меняют форму.

Учитель: Наверно многие из вас задумывались, почему водомерка может свободно перемещаться по поверхности воды, почему росинки, мыльные пузыри, капля в свободном полете, планеты и звезды имеют шарообразную форму, почему одни твердые тела хорошо смачиваются жидкостью, другие плохо, как происходит всасывание питательных элементов, влаги из почвы корневой системой растительности, как происходит кровообращение в живых организмах и т. д. Разгадка этих явлений и многих других привела к открытию удивительного свойства жидкостей – поверхностного натяжения и капиллярных явлений.

Дальше мы будем работать в группах. Каждая группа получит задание, выполняя которое вы познакомимтесь с новыми свойствами жидкостей. Результаты вашей работы вы представите в виде отчета по образцу, который я вам раздам. Затем каждая группа отчитается за проделанную работу. (Количество групп зависит от наполняемости классов, соответственно 2-3 группы выполняют задание1и 2-3 –задание 2)

Задание 1

1. Познакомиться со статьей “Поверхностное натяжение”. Приложение 2

2. Ответить на вопросы:

Какое явление называется поверхностным натяжением?
Где можно наблюдать явление поверхностное натяжение?
Какими величинами характеризуется поверхностное натяжение?

3. Выполнить эксперимент:

“Изучение формы жидкости в естественных условиях”.

Приборы и материалы: алюминиевая, медная, стеклянная, парафиновая пластинки; масло подсолнечное или оливковое; раствор спирта в воде, проволока, шприц или стеклянная трубка.

Ход работы

1. Поместите капли масла и воды на алюминиевую, медную, стеклянную, парафиновую пластинки.

2. Рассмотрите и зарисуйте формы капель.

3. Сделайте вывод о взаимодействии молекул жидкости и твёрдого тела.

4. Результаты занесите в таблицу.

5. Введите с помощью стеклянной трубки или шприца в смесь спирта и воды немного оливкового масла.

6. Рассмотрите поверхность масляной капли.

7. Пропустите через центр масляного шара проволоку и вращайте её.

8. Рассмотрите, как изменяется форма капли.

9. Сделайте вывод о форме поверхности жидкости.

10.Оформите отчет о проделанной работе по образцу:

Дать определение явления, описать величины его характеризующие
Название работы
Цель
Оборудование
Таблица	1
	2
	3
	4
Вывод

Задание 2

1. Познакомиться со статьей “Капиллярные явления”. Приложение 2

2. Ответить на вопросы:

Что такое капиллярные явления?
Где можно наблюдать капиллярные явления?
Какими величинами характеризуются капиллярные явления?

3. Выполнить эксперимент: “Изучение зависимости высоты подъема жидкости от диаметра капилляра, от рода жидкости”.

Цель работы: изучить зависимость подъема жидкости от диаметра капилляра”

Приборы и материалы: стеклянные трубки разного диаметра , вода, линейка, прозрачный сосуд прямоугольной формы.

Ход работы

1. Замерьте диаметр стеклянных трубок и занесите в таблицу.

2. Опустите стеклянные трубки разного диаметра в сосуд с водой.

3. Замерьте высоту поднятия воды в каждой трубке.

4. Результат занесите в таблицу.

3. Сделайте вывод о зависимости высоты поднятия жидкости в трубке от диаметра.

4. Возьмите стеклянные трубки одно диаметра опустите их одновременно в сосуд с водой, с растительным маслом, с спиртом.

5. Замерьте высоту поднятия воды в каждой трубке.

6. Результат занесите в таблицу.

7. Сделайте вывод о зависимости высоты поднятия жидкости в трубке от рода жидкости.

10. Оформите отчет о проделанной работе по образцу. (См. 1 задание)

После выполнения работы по одному представителю от группы выходят к доске и объясняют ход выполнения работы, делают выводы. Класс делает соответствующие записи в тетради.

Сообщения учащихся:

“Смачивание в природе”;
“Капиллярные явления в растительном мире”;
“Кровеносные сосуды”.

Подведение итогов урока.

Учитель: При изучении природных явлений, поведения животных и человека можно найти много практических и интересных явлений. На сегодняшнем уроке мы с вами узнали о свойствах поверхности жидкости, познакомились с капиллярными явлениями и теперь с позиций полученных знаний, вы можете объяснить широкий круг явлений.

Литература.

Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н. Физика (базовый и профильный уровни) 10 класс.- М.: Просвещение, 2010 г.;
Касьянов В.А., 10 класс, М.: Дрофа, 2003 г.

Интернет источники:

http://tims.ucoz.ru/svoistva/smachivanie.html
http://slovari.yandex.ru/~%D0%BA%D0%BD%D0%B8%D0%B3%D0%B8/% D0%91%D0%A1%D0%AD/%D0%9A%D0%B0%D0%BF%D0%B8%D0% BB%D0%BB%D1%8F%D1%80%D0%BD%D1%8B%D0%B5%20%D1% 8F%D0%B2%D0%BB%D0%B5%D0%BD%D0%B8%D1%8F/
http://www.physicexperts.ru/pexps-1085-1.html
http://ru.wikipedia.org/wiki/%C6%E8%E4%EA%EE%F1%F2%FC

xn--i1abbnckbmcl9fb.xn--p1ai

Применение и проявление капиллярности в быту, в природе, в технике

Однажды, когда я заболела, мама решила узнать температуру моего тела и предложила мне померить её с помощью термометра. Первоначально, когда мама подала мне термометр, он показал тридцать шесть градусов. Я его встряхнула, поместила себе в подмышечную впадину и подождала некоторое время. Показания термометра на этот раз составили тридцать семь целых и две десятых градуса. Следовательно, я была больна, и мне пришлось лечиться.

Меня заинтересовала очень тонкая трубка в термометре. Я захотела узнать, как она называется, есть ли такие же тонкие трубки в природе, в технике и ещё в быту. Отгадку подсказала учитель физики. Она рассказала про капилляры и предложила мне изучить капиллярные явления.

Под капиллярными явлениями понимают подъём или опускание жидкости в узких трубках - капиллярах.

Термин «капилляр» происходит от латинского слова capillus-волос.

Капиллярные явления впервые были исследованы Леонардо да Винчи в пятнадцатом веке.

Движение жидкости в капиллярах может быть вызвано разностью капиллярных давлений, возникающей в результате различной кривизны поверхности жидкости. Поток жидкости направлен в сторону меньшего давления: для смачивающих жидкостей - к мениску с меньшим радиусом кривизны. Пониженное, в соответствие с уравнением Кельвина, давление пара над смачивающими менисками является причиной капиллярной конденсации жидкостей в тонких порах.

Отрицательное капиллярное давление оказывает стягивающее действие на ограничивающие жидкость стенки. Это может приводить к объемной деформации высоко дисперсных систем и пористых тел - капиллярной контракции. Так, например происходящий рост капиллярного давления приводит к усадке материалов.

Многие свойства дисперсных систем (проницаемость, прочность, поглощение жидкости) в значительной мере обусловлены капиллярными явлениями, т. к. в тонких порах этих тел реализуются высокие капиллярные давления.

Искривление поверхности жидкостей ведёт к появлению в жидкости дополнительного капиллярного давления ∆р, величина которого связана со средней кривизной r поверхности уравнением Лапласа.

Капиллярное давление создаётся силами поверхностного натяжения, действующими по касательной к поверхности раздела. Искривление поверхности раздела ведёт к появлению составляющей, направленной внутрь объёма одной из контактирующих фаз. Для плоской поверхности раздела такая составляющая отсутствует и ∆р=0.

Капиллярные явления охватывают различные случаи равновесия и движения поверхности жидкости под действием межмолекулярных сил и внешних сил (в первую очередь силы тяжести), в простейшем случае, когда внешние силы отсутствуют или скомпенсированы, поверхность жидкости всегда искривлена. Так, в условиях невесомости, ограниченный объём жидкости, несоприкасающейся с другими телами. Принимает под действием поверхностного натяжения форму шара. Эта форма отвечает устойчивому равновесию жидкости, поскольку преобладает минимальной поверхности при данном объеме, следовательно, поверхностная энергия жидкости в этом случае минимальна. Форму шара жидкость принимает в том случае, если она находится в другой, равной по плотности жидкости (действие силы тяжести компенсируется архимедовой выталкивающей силой).

При не скомпенсированной силе тяжести картина существенно меняется. Маловязкая жидкость (например, вода), взятая в достаточном количестве, принимает форму сосуда, в который она налита. Её свободная поверхность оказывается практически плоской, т. к. силы земного притяжения преодолевают действие поверхностного натяжения, стремящегося искривить и сократить поверхность жидкости.

Однако, по мере уменьшения массы жидкости роль поверхностного натяжения снова становится определяющей: при дроблении жидкости в среде газа или газа в жидкости образуются мелкие капли или пузырьки практически сферической формы.

Свойства систем, состоящих из многих мелких капель или пузырьков (эмульсии, жидкие аэрозоли, пены), и условия их образования во многом определяются кривизной поверхности частиц, то есть капиллярными явлениями.

Не меньшую роль капиллярные явления играют при образовании новой фазы капелек жидкости при конденсации паров, пузырьков пара при кипение жидкостей, зародышей твёрдой фазы при кристаллизации.

В капиллярах изогнутую поверхность при полном смачивании и не смачивании можно принять за полусферу, радиус которой равен радиусу канала трубки r.

Вдоль границ поверхностного слоя, имеющего форму окружности, на стенки трубки действует сила поверхностного натяжения, направленная вниз. По третьему закону Ньютона такая же по модулю сила действует на жидкость со стороны стенок трубки вверх. Эта сила и заставляет жидкость подниматься. Так как длина окружности l=2πr, то эта сила равна F=σ2πr.

Поднятие жидкости в капилляре прекращается, когда сила уравновесится силой тяжести mg, действующей на поднятый столбик жидкости.

Высота поднятия смачивающей жидкости в капилляре равна

2σ h= —

Жидкость, не смачивающая стенки капилляра (например, ртуть в стеклянной трубке), опускается ниже уровня жидкости в широком сосуде.

Глубина h, на которую опускается жидкость, также определяется формулой 2σ h = — .

Капиллярная дефектоскопия. Метод дефектоскопии основан на проникновении некоторых веществ в дефекты изделий под действием капиллярного давления, из-за чего искусственно повышается свето- и цветоконтрастность дефектного участка относительно неповреждённого. Для этого на поверхность изделия наносят люминесцирующее вещество, которое засасывается капиллярами в трещины и другие повреждения поверхности и делает их легко обнаружимыми. Этот метод называют люминесцентной, а иногда и световой дефектоскопией.

Капиллярная химия - устаревшее название физико-химических поверхностных явлениях, входящих, как составная часть, в современную коллоидную химию.

Капиллярная конденсация - это конденсация пара в капиллярах и микротрещинах пористых тел или в промежутках между тесно сближенными твердыми частицами. Сложная капиллярная структура пористого тела может служить причиной капиллярного гистерезиса – зависимости количества сконденсировавшейся в порах жидкости не только от давления пара, но и от предыстории процесса, то есть от того, как было достигнуто данное состояние: в процессе конденсации или же в ходе испарения жидкости.

Капиллярные волны – это волны на поверхности жидкости малой длины. В восстановлении равновесного состояния поверхности жидкости при капиллярных волнах основную роль играют силы поверхностного натяжения.

Капиллярное давление. Разность давлений по обе стороны искривлённой поверхности раздела фаз (жидкость-пар или двух жидкостей), вызванная её поверхностным (межфазным) натяжением.

Капиллярное кровообращение это движение крови в мельчайших сосудах – капиллярах, обеспечивающее обмен веществ между кровью и тканями. Капиллярное кровообращение осуществляется вследствие разности гидростатичных давлений в артериальном и венозном концах капилляра. Давление в артериальном конце равно 30-35 мм. ртутного столба, что на 8-10 мм. превышает онкотическое давление плазмы крови. Под влиянием этой разности давлений вода и многие растворенные в ней вещества ( кроме высокомолекулярных белков) переходят из плазмы крови в тканевую жидкость, приносят к тканям необходимые для жизнедеятельности вещества. По мере продвижения крови по капилляру гидростатичность давления падает и в венозном конце капилляра равна 12-17 мм. ртутного столба, что примерно на 10 мм. ниже онкотического давления крови. Вследствие этого вода и растворенные в ней вещества переходят из тканевой жидкости в плазму. Тем самым обеспечивается удаление продуктов обмена из тканей. Величина капиллярного кровообращения пропорциональна интенсивности обмена веществ. Так, в состоянии покоя, на 1 мм. поперечного сечения скелетной мышцы приходится 30-50 функционирующих капилляров; при интенсивной деятельности мышцы их количество возрастает в 50-100 раз.

1. 2. Применение и проявление капиллярности в быту, в природе и технике.

В быту используется медицинский термометр.

Кирпичные дома в своей нижней части должны быть изолированы от влаги, т. к. кирпичи - пористые тела и хорошо впитывают влагу, а это может привести к ухудшению теплоизоляционных свойств кладки и разрушению.

В природе благодаря многочисленным капиллярам в почве вода поднимается к поверхности и интенсивно испаряется. Это ведёт к потере влаги, необходимой растениям, а чтобы влага не испарялась, землю надо чаще рыхлить, то есть ломать капилляры.

В технике - капиллярные явления применяют как один из способов подвода смазки к деталям машины.

Глава 2. Практическая часть.

2. 1 Описание опытов по изучению явлений капиллярности.

I Опыт. Изучение зависимости между высотой поднятия жидкости h и диаметром капилляра d.

1 шаг: хорошо протерла от жира и пыли сосуд и капиллярные трубки.

2 шаг: налила в сосуд чистой воды из крана.

3 шаг: затем поставила в сосуд капилляр.

Общее у них всех было то, что в каждом капилляре вода поднималась выше уровня воды в сосуде.

А различались они тем, что у каждого из них был разный диаметр отверстия. И поэтому в каждом из них вода поднималась на разную высоту.

d = 7 мм 3 мм d = 5 мм 5 мм d = 3 мм 9 мм

Температура в помещении семнадцать градусов.

Вывод: Чем тоньше капилляр, тем выше высота подъема жидкости.

II Опыт. Изучение зависимости между высотой поднятия жидкости h и характером жидкости.

Вместо воды, которая хорошо смачивает стекло , я взяла жир. Жир стекло смачивает плохо.

Он не поднимается по капилляру, так как не смачивает стекло, так как во взаимодействии его молекул с молекулами стекла преобладает отталкивание. Значит, жир не будет подниматься по капилляру.

Я пыталась определить высоту опускания жира в капилляре: для этого опустила капилляр до дна сосуда и зажала верхнюю часть пальцем, затем вытащила капилляр и измерила высоту столба жидкости в капилляре. Она составила двадцать один мм. Затем измерила высоту жидкости в сосуде, она составила двадцать пять мм.

Вывод. Жидкость, не смачивающая капилляр, на поднимается по нему, а её уровень в капилляре ниже уровня в сосуде.

III Опыт. Определение зависимости между высотой поднятия жидкости h и температурой жидкости t.

Для опыта был выбран капилляр диаметром 4 мм. Измеряя высоту столба жидкости в капилляре через каждые 10 градусов при остывании жидкости, я получила следующие результаты t 300 С 400 С 500 С 600 С 700 С

h 4. 2 мм 4. 4 мм 4. 6 мм 4. 8 мм 5 мм

Если представить в виде графика

Вывод: Между высотой поднятия жидкости в капилляре и её температурой существует линейная зависимость.

ЗАКЛЮЧЕНИЕ

Не было бы счастья, да несчастье помогло: благодаря моей болезни и моей любознательности я познакомилась с очень интересными предметами – тонкими трубочками под названием «капилляры». Я изучила такие интересные явления как поднятие жидкости по капилляру выше уровня основной жидкости в сосуде и опускания жидкости по капилляру ниже уровня основной жидкости в сосуде.

Моё предположение (гипотеза) получило своё подтверждение опытным путем.

Жидкость, находящаяся в капилляре, поднимается (опускается) относительно уровня жидкости в сосуде тем больше (меньше), чем меньше диаметр капилляра и выше температура жидкости.

www.hintfox.com