Энтропия. Второй закон термодинамики Энтропия. Энтропия воды
Второй закон термодинамики. Энтропия. - таблицы Tehtab.ru
Второй закон термодинамики. Энтропия.
Второй закон связан с понятием энтропии, являющейся мерой хаоса (или мерой порядка). Второй закон термодинамики гласит, что для вселенной в целом энтропия возрастает.
Существует два классических определения второго закона термодинамики :
-
Кельвина и Планка
- Клаузиуса
Не существует циклического процесса, который извлекает количество теплоты из резервуара при определенной температуре и полностью превращает эту теплоту в работу. (Невозможно построить периодически действующую машину, которая не производит ничего другого, кроме поднятия груза и охлаждения резервуара теплоты)
Не существует процесса, единственным результатом которого является передача количества теплоты от менее нагретого тела к более нагретому. (Невозможен круговой процесс, единственным результатом которого было бы производство работы за счет охлаждения теплового резервуара)
Оба определения второго закона термодинамики опираются на первый закон термодинамики, утверждающий, что энергия убывает.
Второй закон связан с понятием энтропии (S).
Энтропия порождается всеми процессами, она связана с потерей системы способности совершать работу. Рост энтропии - стихийный процесс. Если объем и энергия системы постоянны, то любое измение в системе увеличивает энтропию. Если же объем или энергия системы меняются, энтропия системы уменьшается. Однако, энтропия вселенной при этом не уменьшается.
Для того, чтобы энергию можно было использовать, в системе должны быть области с высоким и низким уровнями энергии. Полезная работа производится в результате передачи энергии от области с высоким уровнем энергии к области с низким уровнем энергии.
- 100% энергии не может быть преобразовано в работу
- Энтропия может вырабатываться, но не может быть уничтожена
Эффективность теплового двигателя
Эффективность теплового двигателя, действующего между двумя энергетическими уровнями , определена в пересчете на абсолютные температуры
η = ( Th - Tc ) / Th = 1 - Tc / Th
где
η = эффективность
Th = верхняя граница температуры (K)
Tc = нижняя граница температуры (K)
Для того, чтобы достичь максимальной эффективности Tc должна быть на столько низкой, на сколько это возможно. Чтобы эффект был 100% -м, Tc должна равнятся 0 по шкале Kельвина. Практически это невозможно, поэтому эффективность всегда меньше 1 (менее 100%).
- Изменение энтропии > 0 Необратимый процесс
- Изменение энтропии= 0 Двусторонний процесс (обратимый)
- Изменение энтропии < 0 Невозможный процесс (неосуществимый)
Энтропия определяет относительную способность одной системы влиять на другую. Когда энергия двигается к нижнему энергетическому уровню, где уменьшается возможность влияния на окружающую среду, энтропия увеличивается.
Определение энтропии
Энтропия определяется как :
S = H / T
где
S = энтропия (кДж/кг*К)
H = энтальпия (кДж/кг)
T = абсолютная температура (K)
Изменение энтропии системы вызвано изменением содержания темпла в ней. Изменение энтропии равно изменению темпла системы деленной на среднюю абсолютную температуру ( Ta):
dS = dH / Ta
Сумма значений (H / T) для каждого полного цикла Карно равна 0. Это происходит из-за того, что каждому положительному H противостоит отрицательное значение H.
- Тепловой цикл Карно
Цикл Карно— идеальный термодинамический цикл.
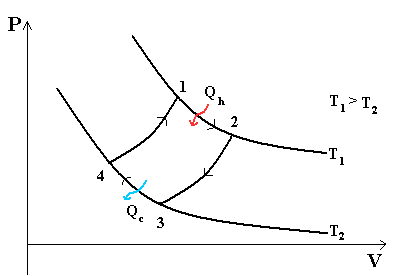
В тепловом двигателе, газ (реверсивно) нагревается (reversibly heated), а затем охлаждается. Модель цика следующая: Положение 1 --( изотермическое расширение) --> Положение 2 --( адиабатическое расширение) --> Положение 3 --(изотермическое сжатие) --> Положение 4 --(адиабатическое сжатие) --> Положение 1
Положение 1 - Положение 2: Изотермическое расширение Изотермическое расширение. В начале процесса рабочее тело имеет температуру Th , то есть температуру нагревателя. Затем тело приводится в контакт с нагревателем, который изотермически (при постоянной температуре) передаёт ему количество теплоты QH. При этом объём рабочего тела увеличивается. QH=∫Tds=Th (S2-S1) =Th ΔSПоложение 2 - Положение 3: Адиабатическое расширение Адиабатическое (изоэнтропическое) расширение. Рабочее тело отсоединяется от нагревателя и продолжает расширяться без теплообмена с окружающей средой. При этом его температура уменьшается до температуры холодильника.Положение 3 - Положение 4: Изотермическое сжатие Изотермическое сжатие. Рабочее тело, имеющее к тому времени температуру Tc, приводится в контакт с холодильником и начинает изотермически сжиматься, отдавая холодильнику количество теплоты Qc. Qc=Tc(S2-S1)=Tc ΔSПоложение 4 - Положение 1: Адиабатическое сжатие Адиабатическое (изоэнтропическое) сжатие. Рабочее тело отсоединяется от холодильника и сжимается без теплообмена с окружающей средой. При этом его температура увеличивается до температуры нагревателя.
При изотермических процессах температура остаётся постоянной, при адиабатических отсутствует теплообмен, а значит, сохраняется энтропия.
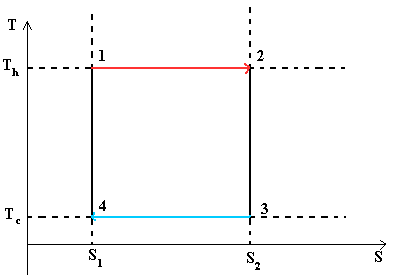
Поэтому цикл Карно удобно представить в координатах T и S (температура и энтропия).
Законы термодинамики были определены эмперическим путем (эксперементально). Второй закон термодинамики - это обощение экспериментов, связанных с энтропией. Известно, что dS системы плюс dS окружающей среды равно или больше 0.
- Энтропия адиабатически изолированной системы не меняется!
Пример - Энтропия при нагревании воды
Процесс нагревания 1 кг воды от 0 до 100oC (273 до 373 K) при нормальных условиях.
Удельная энтальпия для воды при 0oC = 0 кДж/кг (удельная - на единицу массы)
Удельная энтальпия для воды при 100oC = 419 кДж/кг
Изменение удельной энтропии :
dS = dH / Ta
= ((419 кДж/кг) - (0 кДж/кг)) / ((273 К + 373 К)/2)
= 1.297 кДж/кг*К
Пример - Энтропия при испарении воды
Процесс превращения 1 кг воды при 100oC (373 K) в насыщенный пар при 100oC (373 K) при нормальных условиях.
Удельная энтальпия пара при 100oC (373 K) до испарения = 0 кДж/кг
Удельная теплота парообразования 100oC (373 K) при испарении = 2 258 кДж/кг
Изменение удельной энтропии:
dS = dH / Ta
= (2 258 - 0) / ((373 + 373)/2)
= 6.054 кДж/кг*К
Полное изменение удельной энтропии испарения воды - это сумма удельной энтропии воды (при 0oC) плюс удельная энтропия пара (при температуре 100oC).
tehtab.ru
Энтропия - вода - Большая Энциклопедия Нефти и Газа, статья, страница 2
Энтропия - вода
Cтраница 2
При любом давлении и при температуре 0 С энтропии воды s0 равна нулю. С, изображаемая в р, и-координатах линией / ( см. рис. 7 - 1), в Т, s - координатах превращается в точку и обозначается буквой а. Эта точка а находится на оси ординат на 273 С выше абсолютного нуля и служит началом построения нижней пограничной кривой. [16]
При изменении давления р от 0 до 225 ата энтропия воды ( s) увеличивается от 0 до 1 05 ккал кг град, а энтропия сухого пара уменьшается от 2 19 до 1 05 ккал1кг - град. [17]
Изменение энтропии системы при замерзании воды складывается из изменений энтропии воды и резервуара. Если резервуар достаточно велик, то теплота, выделяющаяся при замерзании одного моля воды, изменит его температуру лишь на бесконечно малую величину. [18]
Перечислите экспериментальные данные, которые необходимо получить для определения энтропии газообразной воды при 298 К калориметрически и спектроскопически. Сделайте это, записав уравнение для вычисления S газообразной воды и показав, каким образомэкспериментальные данные обоих типов входят в соответствующие уравнения. [19]
Каждое из этих особых значений влажности образцов характеризуется особым уровнем энтропии воды, постоянным для всех веществ, и определяет специфическое влажностное состояние вещества. Очевидно, что все физические свойства солей и удобрений следует определять в одном из указанных влажностных состояний вещества. [20]
Неточность этой формулы заключается в том, что, как указывалось, энтропия воды при 0 С принята равной нулю и теплоемкость воды Ср1 ккал / кг град. [21]
Рассматриваемые в настоящем сообщении величины ASn ( AS n) характеризуют суммарное изменение энтропии воды как в области ближней, так и в области дальней гидратации иона. [22]
Энтропия гидратации имеет отрицательное значение, так как при упорядочении расположения молекул вокруг иона энтропия воды уменьшается. Величина P &V также незначительна. [23]
Поскольку растворение веществ, усиливающих развитие кластерных структур в воде, связано с уменьшением энтропии воды, растворимость веществ должна быть тем меньше, чем сильнее выражено их влияние на структуру воды в водных растворах. [24]
Подогрев воды в остальных ступенях распределяют по геометрической прогрессии или по методу равного деления энтропии воды по ступеням. [25]
Из спектроскопических данных Киселев и Лыгин ( 1961а) рассчитали колебательную, вращательную и конфигурационную энтропии воды, адсорбированной на гидроксилированной поверхности кремнезема. Для адсорбированной воды были выбраны две модели, в первой из них вода связана водородной связью с одной, - а во второй - с двумя гидроксильными группами. Рассчитанные значения энтропии были меньше, чем экспериментально определенные, что указывает на наличие других степеней свободы подвижности молекул, возможно колебаний параллельно поверхности, дающих вклад в экспериментальные значения энтропии. Аналогичные расчеты были предприняты ( Киселев, Лы-тин, 19616) для случая взаимодействия между поверхностными гидроксильными группами и физически адсорбированным бензолом и к-гексаном. [26]
Из спектроскопических данных Киселев и Лыгин ( 1961 а) рассчитали колебательную, вращательную и конфигурационную энтропии воды, адсорбированной на гидроксилированной поверхности кремнезема. Для адсорбированной воды были выбраны две модели, в первой из них вода связана водородной связью с одной, - а во второй - с двумя гидроксильными группами. Рассчитанные значения энтропии были меньше, чем экспериментально определенные, что указывает на наличие других степеней свободы подвижности молекул, возможно колебаний параллельно поверхности, дающих вклад в экспериментальные значения энтропии. Аналогичные расчеты были предприняты ( Киселев, Лыгин, 19616) для случая взаимодействия между поверхностными гидроксильными группами и физически адсорбированным бензолом и w - гексаном. [27]
В этом случае удобно применять формулы распределения температур либо по геометрической прогрессии, либо по равенству приращений энтропии воды от подогревателя к подогревателю. Последнее распределение совпадает с распределением по геометрической прогрессии в том случае, когда теплоемкость воды принята одинаковой для всех ступеней подогрева. [29]
При температурах выше 400 К давление насыщения, определенное по общим соотношениям термодинамики с использованием значений энтальпии и энтропии идеальной газообразной воды [23], начинает сильно отличаться от фактического. [30]
Страницы: 1 2 3 4
www.ngpedia.ru
Второй закон термодинамики. Энтропия. Определение энтропии. Эффективность теплового двигателя. Тепловой цикл Карно. Неубывание энтропии
2-й закон термодинамики. Энтропия. Определение энтропии. Эффективность теплового двигателя. Тепловой цикл Карно. Неубывание энтропии. Вариант для печати.
Второй закон связан с понятием энтропии, являющейся мерой хаоса (или мерой порядка). Второй закон термодинамики гласит, что для вселенной в целом энтропия возрастает.
Существует два классических определения второго закона термодинамики :
- Кельвина и Планка: Не существует циклического процесса, который извлекает количество теплоты из резервуара при определенной температуре и полностью превращает эту теплоту в работу. (Невозможно построить периодически действующую машину, которая не производит ничего другого, кроме поднятия груза и охлаждения резервуара теплоты)
- Клаузиуса: Не существует процесса, единственным результатом которого является передача количества теплоты от менее нагретого тела к более нагретому. (Невозможен круговой процесс, единственным результатом которого было бы производство работы за счет охлаждения теплового резервуара)
Оба определения второго закона термодинамики опираются на первый закон термодинамики, утверждающий, что энергия убывает. Второй закон связан с понятием энтропии (S).
Энтропия порождается всеми процессами, она связана с потерей системы способности совершать работу. Рост энтропии - стихийный процесс. Если объем и энергия системы постоянны, то любое измение в системе увеличивает энтропию. Если же объем или энергия системы меняются, энтропия системы уменьшается. Однако, энтропия вселенной при этом не уменьшается.
Для того, чтобы энергию можно было использовать, в системе должны быть области с высоким и низким уровнями энергии. Полезная работа производится в результате передачи энергии от области с высоким уровнем энергии к области с низким уровнем энергии.
- 100% энергии не может быть преобразовано в работу
- Энтропия может вырабатываться, но не может быть уничтожена
Эффективность теплового двигателя
Эффективность теплового двигателя, действующего между двумя энергетическими уровнями , определена в пересчете на абсолютные температуры
- η = ( Th - Tc ) / Th = 1 - Tc / Th
- где
- η = эффективность
- Th = верхняя граница температуры (K)
- Tc = нижняя граница температуры (K)
Для того, чтобы достичь максимальной эффективности Tc должна быть на столько низкой, на сколько это возможно. Чтобы эффект был 100% -м, Tc должна равнятся 0 по шкале Kельвина. Практически это невозможно, поэтому эффективность всегда меньше 1 (менее 100%).
- Изменение энтропии > 0 Необратимый процесс
- Изменение энтропии= 0 Двусторонний процесс (обратимый)
- Изменение энтропии < 0 Невозможный процесс (неосуществимый)
Энтропия определяет относительную способность одной системы влиять на другую. Когда энергия двигается к нижнему энергетическому уровню, где уменьшается возможность влияния на окружающую среду, энтропия увеличивается.
Определение энтропии
Энтропия в системе постоянного объема определяется как :
- dS = dH / T
- где
- S = энтропия (кДж/кг*К)
- H = энтальпия (кДж/кг) (иногда вместо dH записывают dQ = количество теплоты, сообщенное системе )
- T = абсолютная температура (K - градусы Кельвина)
Изменение энтропии системы вызвано изменением содержания тепла в ней. Изменение энтропии равно изменению тепла системы деленной на среднюю абсолютную температуру ( Ta):
Тепловой цикл Карно. Цикл Карно— идеальный термодинамический цикл.
dS = dH / Ta Сумма значений (dH / T) для каждого полного цикла Карно равна 0. Это происходит из-за того, что каждому положительному H противостоит отрицательное значение H.
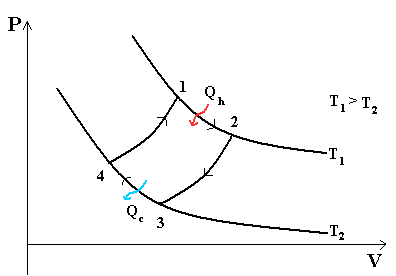
В тепловом двигателе, газ (реверсивно) нагревается (reversibly heated), а затем охлаждается. Модель цика следующая: Положение 1 --( изотермическое расширение) --> Положение 2 --( адиабатическое расширение) --> Положение 3 --(изотермическое сжатие) --> Положение 4 --(адиабатическое сжатие) --> Положение 1
- Положение 1 - Положение 2: Изотермическое расширение
- Изотермическое расширение. В начале процесса рабочее тело имеет температуру Th , то есть температуру нагревателя. Затем тело приводится в контакт с нагревателем, который изотермически (при постоянной температуре) передаёт ему количество теплоты QH. При этом объём рабочего тела увеличивается. QH=∫Tds=Th (S2-S1) =Th ΔS
- Положение 2 - Положение 3: Адиабатическое расширение
- Адиабатическое (изоэнтропическое) расширение. Рабочее тело отсоединяется от нагревателя и продолжает расширяться без теплообмена с окружающей средой. При этом его температура уменьшается до температуры холодильника.
- Положение 3 - Положение 4: Изотермическое сжатие
- Изотермическое сжатие. Рабочее тело, имеющее к тому времени температуру Tc, приводится в контакт с холодильником и начинает изотермически сжиматься, отдавая холодильнику количество теплоты Qc. Qc=Tc(S2-S1)=Tc ΔS
- Положение 4 - Положение 1: Адиабатическое сжатие
- Адиабатическое (изоэнтропическое) сжатие. Рабочее тело отсоединяется от холодильника и сжимается без теплообмена с окружающей средой. При этом его температура увеличивается до температуры нагревателя.
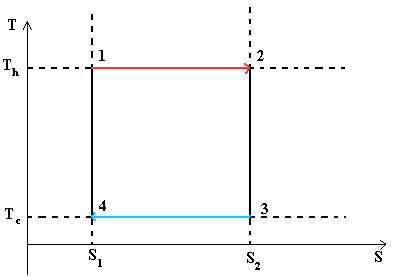
При изотермических процессах температура остаётся постоянной, при адиабатических отсутствует теплообмен, а значит, сохраняется энтропия. Поэтому цикл Карно удобно представить в координатах T и S (температура и энтропия). Законы термодинамики были определены эмперическим путем (эксперементально). Второй закон термодинамики - это обощение экспериментов, связанных с энтропией. Известно, что dS системы плюс dS окружающей среды равно или больше 0 - закон неубывания энтропии. Энтропия адиабатически изолированной системы не меняется!
Пример - Энтропия при нагревании воды
Пример - Энтропия при испарении воды
- Процесс превращения 1 кг воды при 100oC (373 K) в насыщенный пар при 100oC (373 K) при нормальных условиях.
- Удельная энтальпия пара при 100oC (373 K) до испарения = 0 кДж/кг
- Удельная теплота парообразования 100oC (373 K) при испарении = 2 258 кДж/кг
- Изменение удельной энтропии:
- dS = dH / Ta = (2 258 - 0) / ((373 + 373)/2) = 6.054 кДж/кг*К
Полное изменение удельной энтропии испарения воды - это сумма удельной энтропии воды (при 0oC) плюс удельная энтропия пара (при температуре 100oC).
www.dpva.ru
Энтропия — Юнциклопедия
Возможность предсказания направления процессов составляет основное содержание второго закона термодинамики. Немецкий физик Р. Клаузиус проанализировал ограничения, приводящие к односторонности процессов, и ввел функцию S, которую он назвал энтропией. В формулировке Клаузиуса (1865) второй закон термодинамики звучит так: «При самопроизвольных процессах в системах, имеющих постоянную энергию, энтропия всегда возрастает». Таким образом, система самопроизвольно переходит от условий A к условиям B, если SB > SA. В противном случае: — самопроизвольно происходит обратный процесс.
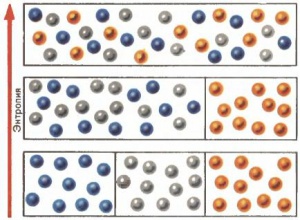 Порядок и беспорядок в мире атомов: энтропия растет с ростом беспорядка.
Порядок и беспорядок в мире атомов: энтропия растет с ростом беспорядка. 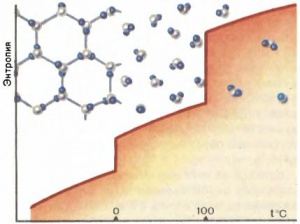 Энтропия водяного пара больше энтропии воды; энтропия воды больше энтропии льда.
Энтропия водяного пара больше энтропии воды; энтропия воды больше энтропии льда. Существуют общие приемы расчета изменений энтропии при различных процессах, связанных с нагревом, охлаждением, плавлением, испарением, химическими реакциями и т. д. Эти приемы, рецепты расчетов составляют неотъемлемую часть термодинамики, и все они основаны на использовании тех или иных опытных данных. Например, чтобы рассчитать изменение энтропии при плавлении ∆Sпл, надо теплоту плавления λ разделить на температуру плавления Tпл. Для плавления 1 моля (18 г) льда λ = 6,02 кДж/моль, а Tпл = 273 К; соответственно ∆Sпл = 22 Дж/моль•град. Энтропия воды больше энтропии льда.
Австрийский физик Л. Больцман ответил на вопрос о физическом смысле энтропии и причинах её роста в изолированных системах (так называют системы, имеющие постоянную энергию). Согласно Больцману, энтропия — мера беспорядка в системе. Полный порядок соответствует минимуму энтропии; любой беспорядок увеличивает её. Таким образом, физический смысл возрастания энтропии следующий: будучи предоставленным самому себе, не испытывая внешних воздействий (изолированная система), коллектив частиц стремится перейти в состояние, в котором при данных условиях возможен больший беспорядок. Максимальная энтропия соответствует полному хаосу.
Спросим себя: где больше порядка в расположении атомов — в кристаллическом твердом теле, где атомы занимают определенные положения (узлы) в кристаллической решетке, или в жидкости, где определенных, закрепленных за ним положений у атома нет? Ответ ясен: в твердом теле. Поскольку энтропия — мера беспорядка, то в жидкости она больше, чем в кристалле; как уже говорилось, энтропия воды больше энтропии льда. Сравним теперь состояние частиц в водяном паре и в воде. Положения молекул не фиксированы и там, и там. Но при комнатной температуре и атмосферном давлении 1 моль воды (18 г) занимает объем 18 см3 (плотность воды составляет 1 г/см3), а 1 моль водяного пара — 22,4 л, т. е. в 1000 раз больше. Где возможен больший беспорядок? Конечно, в паре. И действительно, энтропия пара больше, чем энтропия воды, причем её изменение при испарении больше, чем при плавлении почти в 5 раз: A∆Sпл = 108 Дж/моль•град. Критерий максимума энтропии справедлив только для изолированных тел. Иначе все тела должны были быть газами. Если тело обменивается теплом с окружающей средой, то, согласно Гиббсу, устойчивому состоянию соответствуют наименьшие значения других термодинамических функций (см. Тепловое равновесие). Именно поэтому ниже температуры плавления устойчиво твердое состояние, между температурами плавления и кипения — жидкое и т. д.
Больцман впервые ввел понятие термодинамической «вероятности состояния системы», или числа способов, с помощью которых можно осуществить данное состояние. Согласно Больцману, различные комбинации скоростей и координат молекул, которые могут возникать в системе в результате столкновений между молекулами, не изменяют состояния системы в механическом смысле (энергия системы остается постоянной), но в термодинамическом смысле состояние системы будет изменяться. Всякая система, состоящая из очень большого числа частиц, будет переходить от состояний менее вероятных к состояниям более вероятным, осуществляющимся большим числом способов.
Связь между энтропией S и числом способов реализации данного состояния (термодинамической вероятностью) P дает известная формула Больцмана:
S = klnP + const,
где k = 1,38•10−23 Дж/град — постоянная Больцмана.
yunc.org
Что такое энтропия?
Энтропия – состояние, но не физическое свойство, подобное давлению, температуре или массе. Никакими датчиками невозможно обнаружить энтропию. Это состояние можно лишь просчитать, используя свойства веществ, поддающиеся измерению. Полученные таким способом значения энтропии могут использоваться в других расчетах. Например, связанных с производством пара или электроэнергии, добываемых посредством турбин и машин возвратно-поступательного движения.
Содержимое публикации
Энтропия – состояние текущего времени
Энтропия в какой-то мере является показателем качества, недостатка или достатка энергии. В частности, энтропия показывает, насколько эффективно энергия распространяется от высокотемпературного источника с охватом области, где более низкий уровень температуры.
Этот эффект распространения заставил исследовательские круги охарактеризовать энтропию «стрелкой времени». Если энтропия системы вычисляется при двух разных условиях, тогда условие, при котором энтропия увеличивается, происходит в более позднее время. Увеличение энтропии в системе в целом, всегда проходит в том же направлении, что и течение времени.
 Обобщённое представление процесса с химической точки зрения: 1 — кристаллическое твёрдое вещество; 2 — жидкое состояние; 3 — газообразное состояние; 4 — возрастающая энтропия
Обобщённое представление процесса с химической точки зрения: 1 — кристаллическое твёрдое вещество; 2 — жидкое состояние; 3 — газообразное состояние; 4 — возрастающая энтропияПодобные явления непроизвольно напрашиваются на философскую тему. Однако эти явления не дают помощи для вычислений фактических значений.
Поэтому практическим подходом считают определение энтропии как энергии, которая добавляется в систему или удаляется из системы. Это значение энергии делят на среднюю абсолютную температуру, относительно которой происходит изменение.
Примеры для лучшего понятия
Чтобы лучше понять, как энтропия проявляется на практике, логично рассмотреть простой термодинамический процесс с чайной чашкой, которая была заполнена некоторым количеством воды из чайника, только что снятого с плиты.
Наполненная водой чашка содержит 200 кДж тепловой энергии при 100°C (373ºK). При этом температура воздуха, окружающего заполненную кипятком ёмкость, составляет 20°C. Количество тепла, что останется в конце процесса, составит 40 кДж.
 Эффект транспорта теплообмена с передачей от теплого к холодному: Т1 — среда с более высокой температурой; Т2 — среда с более низкой температурой; Q — тепло; Т — температура
Эффект транспорта теплообмена с передачей от теплого к холодному: Т1 — среда с более высокой температурой; Т2 — среда с более низкой температурой; Q — тепло; Т — температураСогласно второму закону термодинамики, тепло всегда перетекает от горячего тела к более холодному. Для взятого примера, если ёмкость с водой простоит некоторое время, жидкость охладится до той же температуры, что имеет окружающий воздух. Каковы же будут изменения значений энтропии для общего процесса?
Расчёты энтропии для ёмкости с водой
Начальная энтальпия (теплосодержание) чайной чашки = 200 кДж.
Начальная температура воды = 100ºС.
Конечная температура источника тепла = 20ºС.
Средняя абсолютная температура наполненной чаши: Тср = 100 + 20 / 2 = 60ºС (333ºК).
Конечная энтальпия содержимого составит 40 кДж.
Расчёт энтальпии, передаваемой нагретой ёмкостью окружающей среде: 200 – 40 = 160 кДж.
Отсюда энтропия, передаваемая источником тепла окружающей среде, может быть вычислена как значение изменения энтальпии, разделённое на среднюю абсолютную температуру (Тср) в градусах Кельвина: 160 / 333 = — 0,48 кДж/К.
Поскольку имеют место потери тепла в источнике, соответственно изменение энтропии проходит отрицательным значением.
Расчёты энтропии для окружающего воздуха
Начальная температура окружающего воздуха = 20ºС.
В конце процесса теплообмена вода чайной чашки потеряет 160 кДж тепла, тогда как окружающий воздух получит эти 160 кДж. Однако по причине значительного объёма окружающего воздуха, температура атмосферы изменится незначительно.
Энтальпия (теплосодержание), передаваемая водой окружающей среде, имеет в этом эксперименте значение 160 кДж.
Средняя абсолютная температура (Тср) составляет 20ºС или 293ºК.
Отсюда несложно сделать расчёт энтропии окружающего воздуха: 160 / 293 = 0,546 кДж.
Поскольку здесь отмечается восприятие тепла окружающим воздухом, соответственно изменение энтропии имеет положительную тенденцию. Опираясь на этот пример, можно представлять производственные процессы.
В производственном теплообменнике, где, к примеру, используется насыщенный пар на первичной стороне при нагреве воды от 20°C до 60°C, на вторичной стороне пар будет конденсироваться, утрачивая собственное тепло.
Этот процесс наглядно показывает I-s диаграмма зависимости от Рихарда Молье, где точка состояния пара перемещается влево от её начального положения.
Будучи в условиях устойчивого состояния, сухой насыщенный пар конденсируется при постоянном давлении, а точка состояния пара движется вниз по линии постоянного давления.
 Диаграмма Рихарда Молье — полученная немецким тепло-техником из города Дрезден (Германия). Впервые эта диаграмма использовалась для расчётов в 1904 году
Диаграмма Рихарда Молье — полученная немецким тепло-техником из города Дрезден (Германия). Впервые эта диаграмма использовалась для расчётов в 1904 годуКонечно, простым примером с водой в чашке, отдаваемой тепло окружающей среде, невозможно показать все тонкости эффекта энтропии. Тем не менее, этот пример вполне доходчиво разъясняет само понятие.
Всё остальное воспринимается полным циклом уже непосредственно на практике, когда приходится сталкиваться с термодинамическими процессами, протекающими в разных условиях.
Физические величины в помощь к расчётам
Таблица: Относительная плотность и удельная теплоемкость некоторых твердых материалов
| Материал | Относительная плотность | Теплоёмкость, кг/ кДж ºС |
| Алюминий | 2,55 – 2,80 | 0,92 |
| Андалузит | 0,71 | |
| Антимоний | 0,20 | |
| Апатит | 0,83 | |
| Асбест | 2,10 – 2,80 | 0,83 |
| Авгит | 0,79 | |
| Бакелит (древесный) | 1,38 | |
| Бакелит (асбестовый) | 1,59 | |
| Барит | 4,50 | 0,46 |
| Барий | 3,50 | 2,93 |
| Базальт | 2,70 – 3,20 | 0,83 |
| Берилл | 0,83 | |
| Бура | 1,70 – 1,80 | 1,0 |
| Бор | 2,32 | 1,29 |
| Висмут | 9,80 | 0,12 |
| Кадмий | 8,65 | 0,25 |
| Кальцит (0-37ºС) | 0,79 | |
| Кальцит (0-100ºС) | 0,83 | |
| Кальций | 4,58 | 0,62 |
| Карбон | 1,80 – 2,100 | 0,71 |
| Карбид кремния | 0,66 | |
| Касситерит | 0,37 | |
| Цемент застывший | 1,54 | |
| Цемент порошок | 0,84 | |
| Древесный уголь | 1,0 | |
| Халькопирит | 0,54 | |
| Хром | 7,10 | 0,50 |
| Глина | 1,80 – 2,60 | 0,92 |
| Уголь каменный | 0,64 – 0,93 | 1,08 – 1,54 |
| Кобальт | 8,90 | 0,46 |
| Бетон застывший | 0,79 | |
| Бетон обожжённый | 0,75 | |
| Медь | 8,80 – 8,95 | 0,37 |
Таблица: Удельная теплоемкость газов и паров
| Газ или пар | Теплоёмкость, кДж/кг ºС |
| Ацетон | 1,31 |
| Воздух, 0ºС | 1,00 |
| — 100ºС | 1,01 |
| — 200ºС | 1,03 |
| — 300ºС | 1,05 |
| — 400ºС | 1,07 |
| — 500ºС | 1,09 |
| Спирт С2H5OH | 1,66 |
| — Ch4OH | 1,53 |
| Аммоний | 1,76 |
| Аргон | 0,30 |
| Бензол C6H6 | 0,98 |
| Бром | 0,19 |
| Углекислый газ | 0,62 |
| Угарный газ | 0,71 |
| Дисульфит углерода | 0,55 |
| Хлор | 3,43 |
| Хлороформ | 0,54 |
| Эфир | 1,95 |
| Соляная кислота | 0,56 |
| Водород | 10,00 |
| Сульфит водорода | 0,79 |
| Метан | 1,86 |
| Азот | 0,71 |
| Оксид азота | 0,69 |
| Тетраоксид азота | 4,59 |
| Кислород | 0,65 |
| Диоксид серы | 0,49 |
| Пар насыщенный 0,5 АТИ | 1,99 |
| — 2 АТИ | 2,13 |
| — 10 АТИ | 2,56 |
| Пар 0,5 АТИ 150ºС | 1,95 |
| Пар 2 АТИ 200ºС | 2,01 |
| Пар 10 АТИ 250ºС | 2,21 |
Открытия молодости и беспорядок Вселенной
Некоторые материалы взяты на: Pointing.spiraxsarco
zetsila.ru
Энтропия - вода - Большая Энциклопедия Нефти и Газа, статья, страница 3
Энтропия - вода
Cтраница 3
При обратимости процесса должно быть: А50 - AS, где Д51 - Я / Г - изменение энтропии воды при замерзании. [31]
Еще резче зависимость структуры воды от температуры обнаруживается при рассмотрении рядов сравнительного действия различных катионов на неидеальные доли относительных парциальных мо-ляльных энтропии воды при 25 и при 2 или - 6 С. При этом, например, ион Со2 при 25 во всем интервале концентраций стабилизирует уже расшатанную тепловым движением структуру, а при 2, напротив, нарушает ее. Ион NHt очень мало влияет на упорядоченность воды при всех температурах, что можно поставить в связи с обнаруженной Фаянсом и Джонсоном [428] близостью парциальных моляльных объемов ионов NH, СГ и молекулы воды. В результате внедрение этих ионов должно мало нарушать структуру воды. [32]
В процедуре ПАР имеется обращение к процедуре TS ( p), IS ( p), SS ( p) для расчета температуры насыщенного пара, энтальпии и энтропии воды на линии насыщения. [33]
Определите изменение энергии Гиббса ( изобар-но-изотермического потенциала) при равновесной конденсации 1 кмоль водяного пара при 373 К и давлении 1 0133 - 105 Па, если теплота испарения воды равна 40 7 - 106 Дж / кмоль, а изменение энтропии воды при испарении 109 - 103 Дж / кмоль-град. [34]
В приводимых ниже примерах иллюстрирующих применение диаграммы i - х, использованы следующие обозначения: t и / м - температура сухого и мокрого термометра, С; tp - точка росы, С; х - влагосодержание, кг воды / кг сухого воздуха; Ах - приращение или потеря влаги потоком воздуха, кг воды / кг сухого воздуха; р - относительная влажность в долях или процентах; i - энтальпия при насыщении, дж / кг сухого воздуха; i - a - энтропия воды, прибавленной к системе или отнятой от нее, дж / кг сухого воздуха; q - тепло, введенное в систему, дж / кг сухого воздуха; q - - тепло, отнятое от системы, дж / кг сухого воздуха. [35]
Разброс значений энтропии может быть обусловлен многими причинами, но важной является упомянутый выше второй фактор, а именно сольватация. Энтропия воды ( сольватирующей полярное переходное состояние) несомненно будет ниже в чистой воде, чем в смешанном растворителе, где к ней прибавляется энтропия смешения. Однако детальная картина сольватационной ячейки начального и переходного состояний для каждого механизма и каждого индивидуального субстрата в данном растворителе будет различной, что и обусловливает изменения энтропии активации при переходе от одного случая к другому. [36]
Согласно второму закону термодинамики, любой самопроизвольный процесс приводит к возрастанию энтропии Вселенной. Однако энтропия воды при замерзании уменьшается. Объясните, почему оба утверждения не противоречат друг другу. [37]
Вода, как предполагают ученые, приобретает некоторую структуру и образует что-то вроде каркаса или кристаллической решетки вокруг каждого иона. Понижение энтропии воды сказывается на суммарной энтропии всей системы кристалл - вода и приводит к прекращению растворения. К таким структурирующим ионам относятся в основном ионы с сильным электростатическим полем - F -, SO. Соединения, где как катион, так и анион проявляют структурирующие свойства, часто оказываются трудно растворимыми. [38]
Конечно, точно учесть этот вклад нельзя, по для оценки попытаемся рассуждать следующим образом. Считаем, что энтропия воды в низкотемпературной р-фазе коллагена ( 5р) совпадает со значением энтропии соответствующего количества льда. Тогда энтропия той же воды в высокотемпературной а-модификации коллагена ( Sa) заведомо окажется ниже энтропии эквивалентного количества свободной воды по двум причинам. Во-первых, поверхностный слой воды, осуществляющий контакт между гидратной оболочкой и белком, находится в упорядоченном состоянии как выше, так и ниже перехода и, следовательно, вклада в изменение энтропии AS и А. [39]
Поры геля слишком малы для образования кристалликов льда при температуре выше - 78 С, поэтому обычно лед в них не образуется. С понижением температуры вследствие разной энтропии воды геля и льда вода геля приобретает потенциальную энергию, позволяющую ей двигаться по капиллярам, содержащим лед. Диффузия воды геля приводит к росту кристаллов льда и к расширению цементного камня. [40]
Следовательно, имеет место уменьшение энтропии воды, составляющее около 3 кал / град в расчете на 1 моль растворенной соли. Изменения теплосодержания, свободной энергии и энтропии, сопровождающие растворение электролита, будут рассмотрены ниже. [41]
Не только гидрофобные, но и электростатические солевые связи в белках стабилизуются водным окружением, так как при их образовании освобождаются ориентированные молекулы воды, окружающие заряженные группы. Тем самым возникновение солевой связи сопровождается увеличением энтропии воды. Этот выигрыш в свободной энергии более значителен, чем определяемый электростатическим притяжением зарядов. Однако воздействие воды на солевую связь отлично от гидрофобного - солевые связи усиливаются, а гидрофобные ослабляются при добавлении неводных растворителей. [43]
Солевые связи в белках также стабилизируются водным окружением, так как при их образовании освобождаются ориентированные молекулы воды, окружающие заряженные группы. Тем самым появление солевой связи сопровождается увеличением энтропии воды. [44]
Страницы: 1 2 3 4
www.ngpedia.ru
Энтропия. Второй закон термодинамики Энтропия
На основании первого начала термодинамики невозможно установить, в каком направлении и до какого предела будет протекать тот или иной процесс, связанный с превращением энергии.
Из наблюдений над естественными явлениями в природе известно, что многие из них осуществляются самопроизвольно(т.е. без внешних воздействий) только в определенном направлении.
Так, теплота передается от более нагретого тела к менее нагретому, газ распространяется из области высокого давления в область низкого, вода стекает по склону только вниз, а не наоборот. В обратном направлении указанные процессы идти не могут, т.к. требуют приложения энергии извне. В связи с этим они являются несамопроизвольными.
Характерной особенностью многих самопроизвольных процессов является то, что их протекание сопровождается уменьшением внутренней энергии или энтальпии системы. Это утверждение справедливо и для большинства химических реакций, которые, как правило, являются экзотермическими, если протекают сами по себе.
Наблюдаемые закономерности можно объяснить, если предположить, что любая система из всех разрешенных ей состояний стремится занять то, в котором будет обладать наименьшим (из возможных для нее) значением внутренней энергии или энтальпии. При этом данное состояние для системы будет наиболее устойчивым.
Однако предсказать направленность самопроизвольного протекания физических и химических процессов только за счет стремления системы к достижению минимального значения своей внутренней энергии удается не всегда, т.к. известны многие физические явления и эндотермические химические реакции, которые идут самопроизвольно, но внутренняя энергия системы при этом возрастает.
Примерами таких процессов являются: растворение в Н2О некоторых твердых солей (NН4NО3,NаСl,KNO3), распад угольной кислоты на газообразный СО2и жидкую Н2О.
Очевидно, существует еще какая-то причина или мотив, влияющие на возможность осуществления тех или иных явлений. Опытным путем установлено, что таким другим поводом для самопроизвольного протекания процессов в природе является стремление системы к максимальному беспорядку, т.е. к достижению неупорядоченного состояния, которое при данных условиях будет для нее наиболее вероятным (рис. 10).
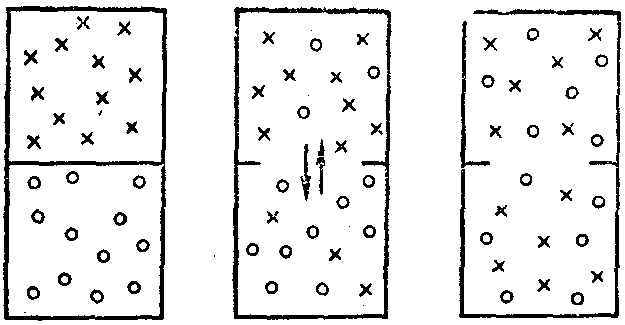
Рис. 10. Схема, иллюстрирующая самопроизвольный процесс выравнивания концентрации
В связи с этим вводится новая термодинамическая функция энтропия (S),являющаяся мерой упорядоченности системы или мерой вероятности достижения ею того или иного состояния.
Термодинамические системы представляют собой совокупность огромного числа структурных единиц вещества: молекул, ионов, атомов, которые участвуют одновременно в различных видах движения: поступательном, вращательном, колебательном и т.д.
Ранее было показано, что любое состояние системы можно описать как с помощью набора ее макроскопических параметров, так и микроскопических. Причем последние учитывают свойства не всей системы в целом, а каждой ее отдельной структурной единицы, т.е. ее расположение в пространстве, скорость и направление движения, характер этого движения, способ и меру взаимодействия с соседними частицами и т.д. Вследствие теплового движения частиц значения их микроскопических параметров будут постоянно изменяться во времени даже в том случае, если макроскопические параметры системы останутся неизменными, вследствие достижения ею равновесного состояния.
Многочисленные наблюдения позволили сделать вывод, что чем большим числом различных микросостояний структурных единиц вещества может быть описано данное макросостояние системы, тем больше вероятность его осуществления и большее значение при этом примет энтропия самой системы.
Принято, что энтропия чистых веществ, существующих в виде идеальных кристаллов при температуре абсолютного нуля (0оK или –273оС), равна нулю. Это значит, что в данном случае достигается полная упорядоченность системы, в результате чего всякое движение частиц в узлах кристаллической решетки станет невозможным. Таким образом, данное макросостояние системы может быть реализовано только одним определенным расположением структурных единиц друг относительно друга (иначе говоря, лишь одним их микросостоянием).
При повышении температуры число возможных микросостояний частиц возрастает, т.к. появляются и усиливаются колебательные и вращательные движения атомов, ионов или молекул в узлах кристаллической решетки. В связи с этим число возможных вариантов их расположения друг относительно друга тоже увеличивается.
Энтропия системы возрастает не только с повышением температуры, но и при плавлении либо сублимации твердого вещества, кипении жидкости. Сопровождаются увеличением энтропии и процессы расширения газа, растворения кристаллов, химического взаимодействия, протекающего с увеличением числа молекул либо других структурных единиц вещества.
Все процессы, связанные с увеличением упорядоченности системы: охлаждение, кристаллизация из раствора либо расплава, конденсация газа, сжатие газа, химические реакции, протекающие с уменьшением числа структурных единиц вещества (полимеризация, поликонденсация) – наоборот, сопровождаются уменьшением энтропии.
Так как энтропия системы пропорциональна числу ее равновероятных микросостояний (W), то, согласно уравнению Больцмана, она может быть численно определена следующим образом:
S=k·lgW,
где k – коэффициент пропорциональности, называемый иначе константой Больцмана. Он имеет значение 1,38 · 10–23 Дж/K и рассчитывается по формуле:
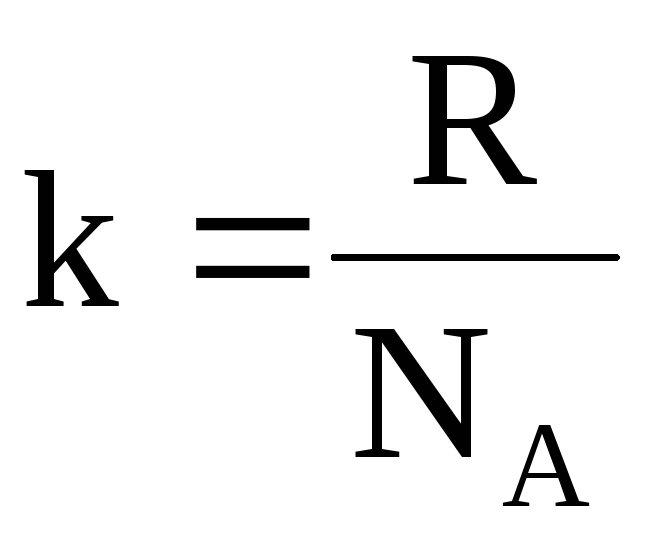 ,
,
где R – универсальная газовая постоянная;
NA – число Авогадро.
Однако таким образом определить значение энтропии для термодинамической системы нельзя, т.к. не представляется возможным учесть и сосчитать все ее микроскопические состояния.
В 1865 г. Клаузиус предложил другую трактовку понятия энтропии.
Р удольф Клаузиус (1822–1888).
удольф Клаузиус (1822–1888).
Немецкий физик. Ввел понятие энтропии. Обобщив работы Карно, Р. Клаузиус определил функцию S, которая зависит только от начального и конечного состояния обратимого процесса и dS = 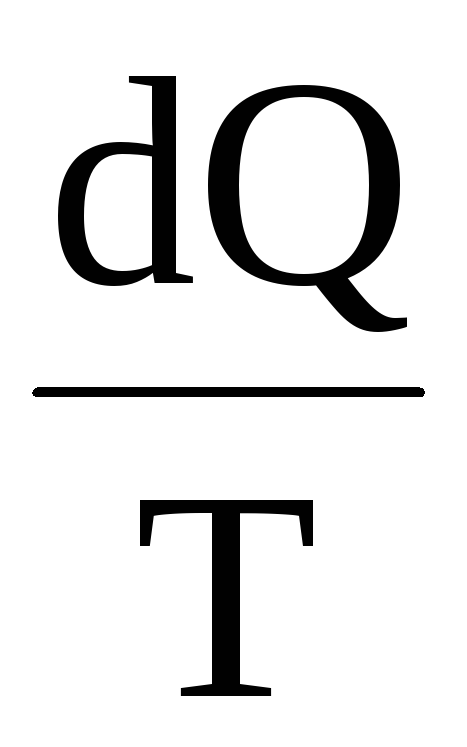 . При этом он писал: «Предлагаю величину S назвать энтропией от греческого – преобразование. Я специально так подобрал слово энтропия, чтобы оно было созвучно со словом энергия, так как эти две величины настолько сходны по своему физическому значению, что созвучие их кажется мне полезным».
. При этом он писал: «Предлагаю величину S назвать энтропией от греческого – преобразование. Я специально так подобрал слово энтропия, чтобы оно было созвучно со словом энергия, так как эти две величины настолько сходны по своему физическому значению, что созвучие их кажется мне полезным».
Он исходил из того, что движение частиц в любой системе может быть упорядоченным и неупорядоченным. Между этими двумя видами движения существует принципиальная разница.
Упорядоченное движениеспособно полностью превращаться в неупорядоченное, а переход неупорядоченного движения в упорядоченное никогда не бывает полным. Причина разности между двумя типами движения связана с неодинаковой вероятностью осуществления каждого из них.
Внутренняя энергия идеального газа полностью (а в других системах в значительной степени) определяется неупорядоченным тепловым движением молекул. В то же время совершение работы всегда требует упорядоченного (направленного) движения частиц вещества. Поэтому принципиально невозможно всю внутреннюю энергию системы использовать для совершения работы. Иными словами – любая форма энергии может перейти в теплоту, но теплота преобразуется в другие формы энергии только частично.
Естественность хаотического движения молекул является причиной того, что различные виды энергии стремятся самопроизвольно перейти в теплоту, а теплота передается менее нагретым телам.
Таким образом, запас внутренней энергии системы можно представить в виде двух слагаемых. Ту часть внутренней энергии, которую можно использовать для совершения работы, по предложению Гельмгольца назвали свободной энергией, остальную часть внутренней энергии, которую даже в принципе нельзя превратить в работу, назвали связанной энергией.Она может превращаться только в теплоту и рассеиваться.
Свободная энергия в любой системе заключена в виде потенциальной энергии. По мере совершения системой работы величина ее свободной энергии убывает. Так, более разреженный газ содержит меньше свободной энергии и больше связанной, чем сжатый газ при одной и той же температуре. Следовательно, сжатый газ способен совершить больше полезной работы.
Величина связанной или «обесцененной» части внутренней энергии тем больше, чем меньше разность температур в системе между отдельными ее частями и выше степень неупорядоченности молекул в ней. Таким образом, при самопроизвольных процессах количество свободной энергии в системе должно уменьшаться, а связанной, наоборот, увеличиваться.
Мерой изменения связанной энергии при переходе системы из одного состояния в другое Клаузиус предложил считать изменение ее энтропии. Он показал, что для изотермических обратимых процессов изменение энтропии равняется тепловому эффекту процесса, деленному на температуру системы (в градусах Кельвина):
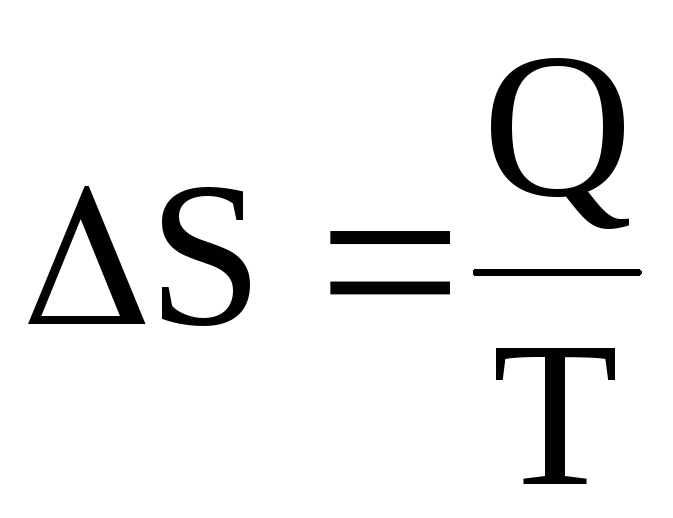
Для изобарных процессов, в ходе которых температура системы изменяется от Т1до Т2и ее агрегатное состоянии остается одним и тем же, ΔSопределяется более сложным образом:
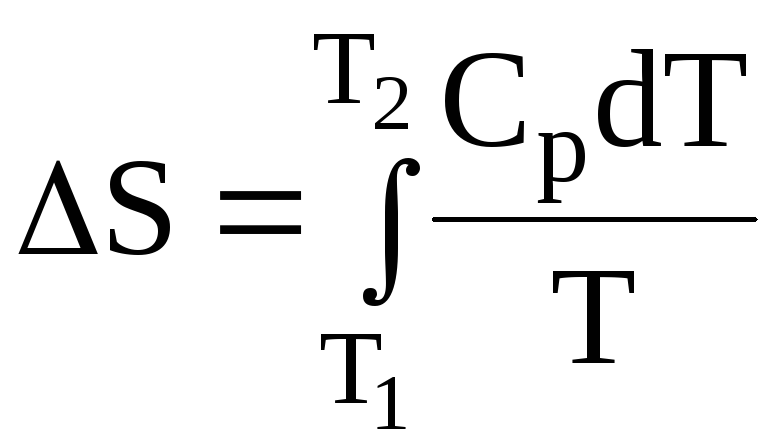
При этом, если Т1= 0; то ΔS=SТ–S0,
где S0 – энтропия системы при абсолютном нуле; SТ – энтропия системы при температуре Т.
Если S0= 0, то ΔS=SТ, а значит
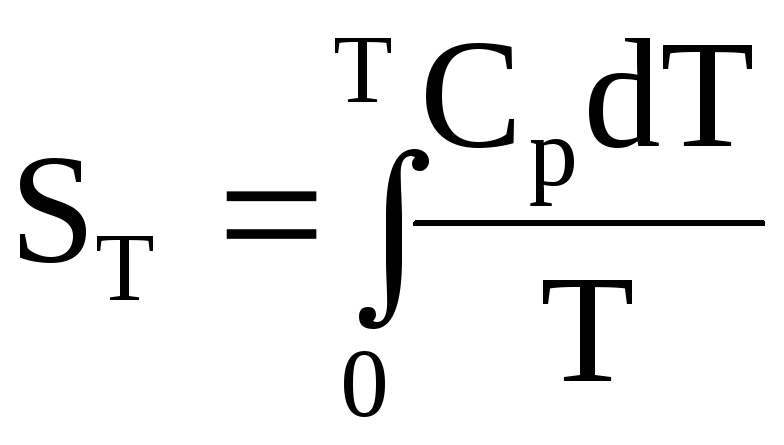
Верхнее выражение позволяет рассчитать энтропию при любой температуре, если известна зависимость изобарной теплоемкости системы (Ср) от температуры в интересующем нас интервале. При температуре плавления и температуре кипения энтропия вещества увеличивается скачкообразно (рис. 11) и ее прирост ΔSможно рассчитать по формуле
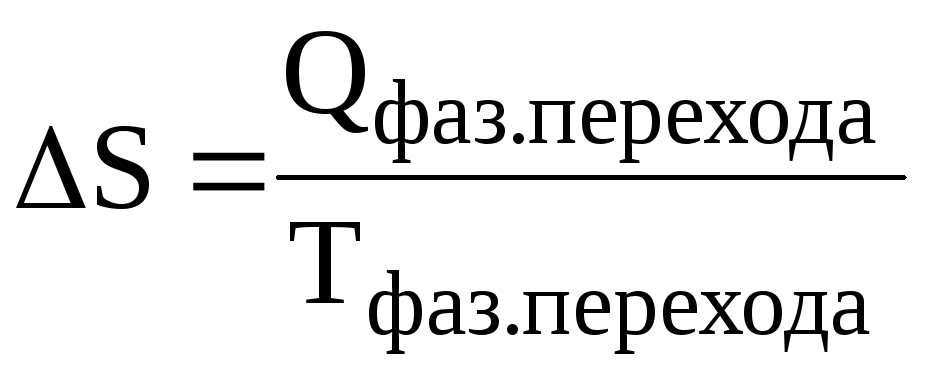
где Qфаз. перехода – теплота, затраченная на плавление или кипение вещества; Тфаз. перехода – температура плавления или кипения вещества.
В общем случае энтропию любого вещества при некоторой температуре Т можно рассчитать по формуле
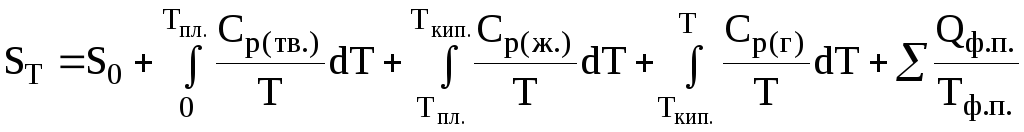
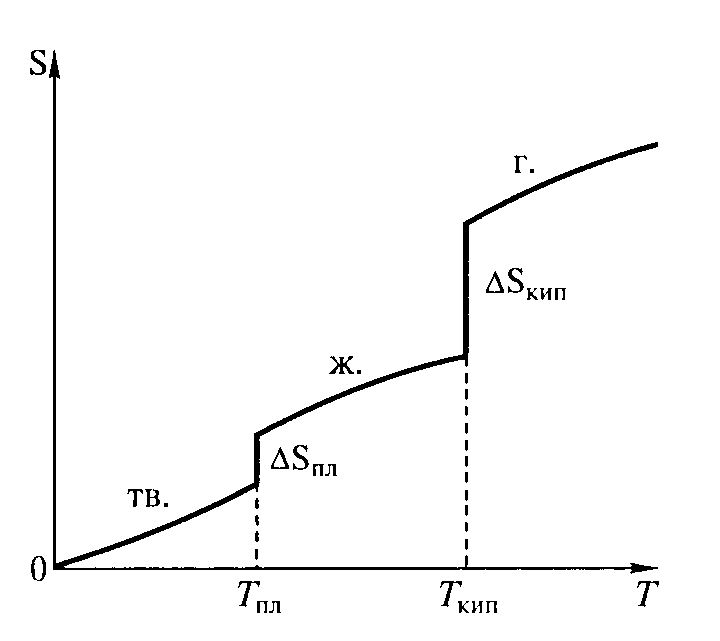
Рис. 11. Зависимость энтропии некоторого вещества от температуры (тв. – твердое вещество; ж. – жидкость; г. – газообразное вещество)
Энтропию вещества, найденную таким образом (т.е. относительно S0 = 0), называют абсолютной энтропией.
Значения энтропии различных чистых веществ, определенные в расчете на один их моль или для растворов веществ с молярной концентрацией 1 моль/дм3 при Т = 298K и р = 101,325 кПа называютсястандартными энтропиями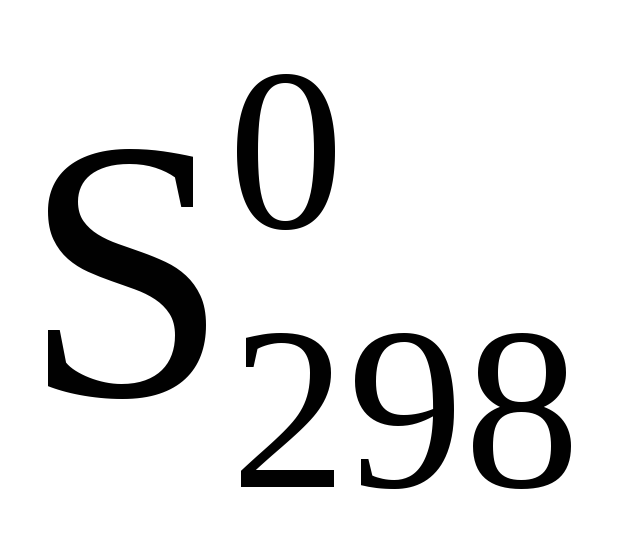 и являются справочными величинами (табл. 3).
и являются справочными величинами (табл. 3).
Единица измерения энтропии для вещества (так называемая «энтропийная единица» или сокращенно – э.е.) имеет размерность Дж/моль · K.
Изменение энтропии при протекании какой-либо химической реакции можно вычислить таким же способом, как и изменение энтальпии, т.е. из суммы энтропий продуктов реакции следует вычесть сумму энтропий исходных веществ (с учетом стехиометрических коэффициентов):
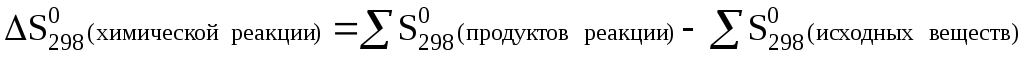
Например, для химической реакции:
4Nh4(г)+ 3O2(г)= 2N2(г)+ 6h3O(ж)
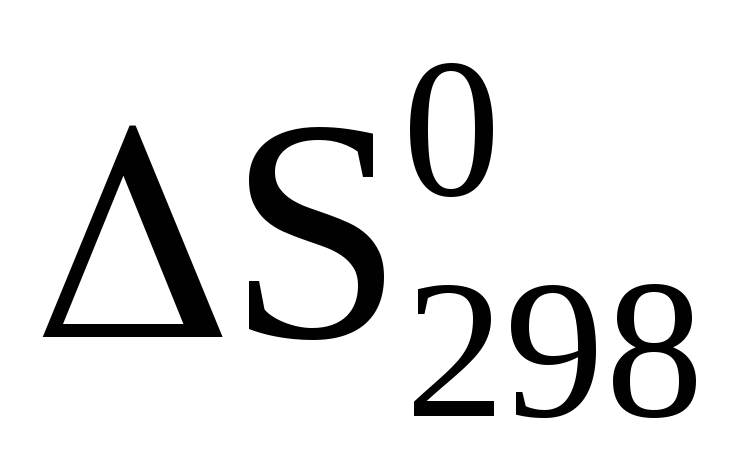 = (
= (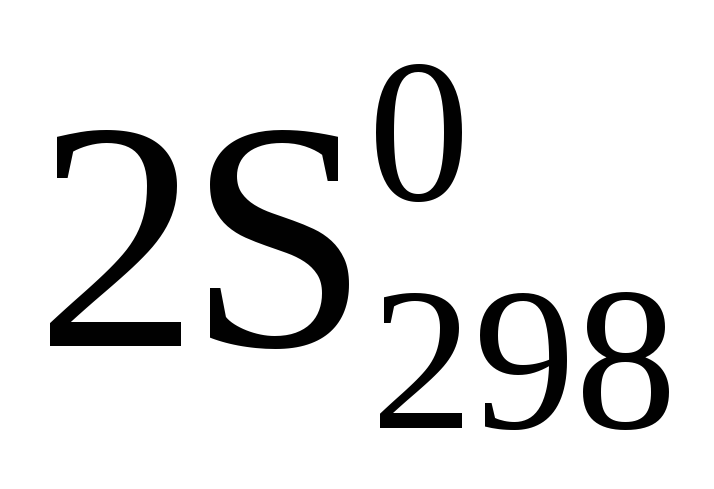 (N2(г)) +
(N2(г)) + 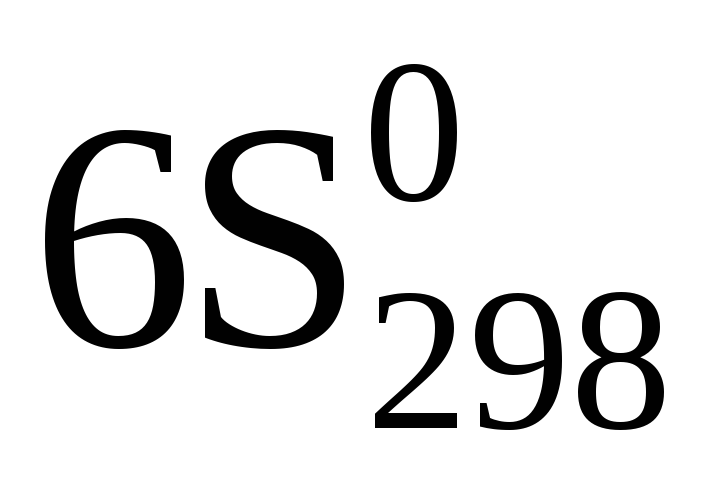 (h3O(ж)) – (
(h3O(ж)) – ( (O2(г)) +
(O2(г)) + 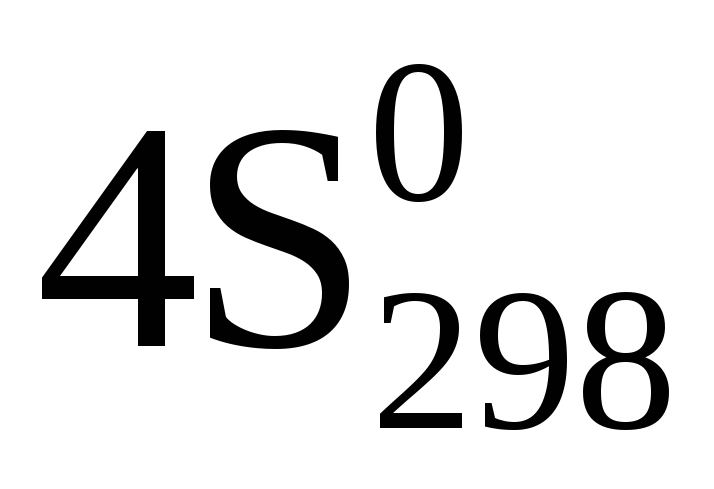 (Nh4(г))
(Nh4(г))
Таблица 3.Стандартные энтропии некоторых веществ (Дж/моль • К)
| Вещество | S°298 | Вещество | S°298 | Вещест-во | S°298 | Вещество | S°298 |
| Al (г.) Al (тв.) Al3+ (р.) AlCl3(тв.) AlBr3(тв.) Al2O3(тв.) Fe (г.) Fe (тв.) Fe3+(р.) FeO (тв.) Fe2O3 (тв.) NaCl (тв.) | 164,4 28,35 -301 109,3 180,2 50,92 180,4 27,15 -309,3 60,75 87,4 72,12 | Cl2(г.) Cl (г.) Cl-(р.) HCl(г.) HCl(р.) ClO2(г.) Cl2O(г.) Br2 (г.) Br2 (ж.) HBr (г.) HI (г.) CaO(тв.) | 229,9 165,1 56,54 186,8 56,5 257,0 266,2 245,5 152,2 198,6 206,5 39,7 | N2 (г.) Nh4 (г.) Nh5+(р.) Nh5Cl(тв.) NO (г.) NO2 (г.) N2O4 (г.) HNO3(г.) NO3-(р.) Pбел (тв.) Pкрас (тв.) CO2 (г.) | 199,9 192,6 114,4 95,8 210,6 240,1 304,3 266,9 147,3 41,1 22,8 213,68 | h3O (г.) h3O(ж.) h3O(тв.) h3 (г.) H+(р.) OH-(р.) O2 (г.) O3 (г.) SO2(г.) SO3 (г.) h3S(г.) CaCO3(тв.) | 188,72 70,08 39,33 130,6 0 -10,87 205,04 238,8 248,1 256,4 205,7 92,9 |
Энтропия является функцией состояния (ее изменение не зависит от пути процесса) и экстенсивным свойством системы (т.е. общая энтропия системы равна сумме энтропий ее составных частей).
В изолированных системах самопроизвольно могут протекать только те процессы, которые сопровождаются увеличением энтропии. Это означает, что состояние устойчивого термодинамического равновесия в такой системе возникает в том случае, если величина ее энтропии достигает своего максимально возможного значения.
Для неизолированных, т.е. закрытых и открытых систем только изменение энтропии, как и изменение одной внутренней энергии, уже не является критерием возможности самопроизвольного протекания процесса.
studfiles.net



















