4. Турбулентное течение жидкости. Турбулентность воды

Турбулентность | Наука | FANDOM powered by Wikia

Турбуле́нтность, устар. турбуле́нция (лат. turbulentus — бурный, беспорядочный), турбуле́нтное тече́ние — явление, заключающееся в том, что при увеличении интенсивности течения жидкости или газа в среде самопроизвольно образуются многочисленные нелинейные фрактальные волны и обычные, линейные различных размеров, без наличия внешних, случайных, возмущающих среду сил и/или при их присутствии. Для расчёта подобных течений были созданы различные модели турбулентности.

Турбулентность экспериментально открыта английским инженером Рейнольдсом в 1883 году при изучении течения несжимаемой жидкости (воды) в трубах.

В гражданской авиации вхождение в зону высокой турбулентности называют воздушной ямой.

Мгновенные параметры потока (скорость, температура, давление, концентрация примесей) при этом хаотично колеблются вокруг средних значений. Зависимость квадрата амплитуды от частоты колебаний (или спектр Фурье) является непрерывной функцией.

Для возникновения турбулентности необходима сплошная среда, которая подчиняется кинетическому уравнению Больцмана или Навье-Стокса или пограничного слоя. Уравнение Навье-Стокса (в него входит и уравнение сохранения массы или уравнение неразрывности) описывает множество турбулентных течений с достаточной для практики точностью.

Обычно турбулентность наступает при превышении некоторого критического числа Рейнольдса и/или Релея (в частном случае скорости потока при постоянной плотности и диаметре трубы и/или температуры на внешней границе среды).

В частном случае, она наблюдается во многих потоках жидкостей и газов, многофазных течениях, жидких кристаллах, квантовых Бозе- и Ферми- жидкостях, магнитных жидкостях, плазме и любых сплошных средах (например, в песке, земле, металлах). Турбулентность также наблюдается при взрывах звёзд, в сверхтекучем гелии, в нейтронных звёздах, в лёгких человека, движении крови в сердце, при турбулентном (т. н. вибрационном) горении.

Она возникает самопроизвольно, когда соседние области среды следуют рядом или проникают один в другой, при наличии перепада давления или при наличии силы тяжести, или когда области среды обтекают непроницаемые поверхности.

Она может возникать при наличии вынуждающей случайной силы. Обычно внешняя случайная сила и сила тяжести действуют одновременно. Например, при землетрясении или порыве ветра падает лавина с горы, внутри которой течение снега турбулентно.

Турбулентность, например, можно создать:

• увеличив число Рейнольдса (увеличить линейную скорость или угловую скорость вращения потока, размер обтекаемого тела, уменьшить первый или второй коэффициент молекулярной вязкости, увеличить плотность среды) и/или число Релея (нагреть среду) и/или увеличить число Прандтля (уменьшить вязкость).

• и/или задать очень сложный вид внешней силы (примеры: хаотичная сила, удар). Течение может не иметь фрактальных свойств.

• и/или создать сложные граничные и/или начальные условия, задав функцию формы границ. Например, их можно представить случайной функцией. Например: течение при взрыве сосуда с газом. Можно, например, организовать вдув газа в среду, создать шероховатую поверхность. Использовать разгар сопла. Поставить сетку в течение. Течение может при этом не иметь фрактальных свойств.

• и/или создать квантовое состояние. Данное условие применимо только к изотопу гелия 3 и 4. Все остальные вещества замерзают, оставаясь в нормальном, не квантовом состоянии.

• облучить среду звуком высокой интенсивности.

• с помощью химических реакций, например горения. Форма пламени, как и вид водопада может быть хаотичной.

При больших числах Рейнольдса, скорости потока от небольших изменений на границе зависят слабо. Поэтому при разных начальных скоростях движения корабля формируется одна и та же волна перед его носом, когда он движется с крейсерской скоростью. Нос ракеты обгорает и создаётся одинаковая картина разгара, несмотря на разную начальную скорость.

Фрактальный — означает самоподобный. Например, ваша рука имеет ту же величину фрактальной размерности, как и у ваших предков и потомков. У прямой линии фрактальная размерность равна единице. У плоскости равна двум. У шара трём. Русло реки имеет фрактальную размерность больше 1, но меньше двух, если рассматривать его с высоты спутника. У растений фрактальная размерность вырастает с нуля до величины больше двух. Есть единица измерения геометрических фигур, называется фрактальная размерность. Наш мир нельзя представить в виде множества линий, треугольников, квадратов, сфер и других простейших фигур. И фрактальная размерность позволяет быстро характеризовать геометрические тела сложной формы. Например, у осколка снаряда.

Нелинейная волна — волна, которая обладает нелинейными свойствами. Их амплитуды нельзя складывать при столкновении. Их свойства сильно меняются при малых изменениях параметров. Нелинейные волны называют диссипативными структурами. В них нет линейных процессов дифракции, интерференции, поляризации. Но есть нелинейные процессы, например, самофокусировка. При этом резко, на порядки увеличивается коэффициент диффузии среды, перенос энергии и импульса, сила трения на поверхность.

То есть, в частном случае, в трубе с абсолютно гладкими стенками при скорости выше некоторой критической, в течение любой сплошной среды, температура которой постоянная, под действием только силы тяжести всегда самопроизвольно образуются нелинейные самоподобные волны и затем турбулентность. При этом нет никаких внешних возмущающих сил. Если дополнительно создать возмущающую случайную силу или ямки на внутренней поверхности трубы, то турбулентность также появится.

В частном случае нелинейные волны — вихри, торнадо, солитоны и другие нелинейные явления (например, волны в плазме — обычные и шаровые молнии), происходящие одновременно с линейными процессами (например акустическими волнами).

На математическом языке турбулентность означает, что точное аналитическое решение дифференциальных уравнений в частных производных сохранений импульса и сохранения массы Навье-Стокса (это закон Ньютона с добавлением сил вязкости и сил давления в среде и уравнение неразрывности или сохранения массы) и уравнение энергии представляет собой при превышении некоторого критического числа Рейнольдса, странный аттрактор. Они представляют нелинейные волны и обладают фрактальными, самоподобными свойствами. Но так как волны занимают конечный объём, какая-то часть области течения ламинарно.

При очень малом числе Рейнольса — это всем известные линейные волны на воде небольшой амплитуды. При большой скорости мы наблюдаем нелинейные волны цунами или обрушение волн прибоя. Например, крупные волны за плотиной распадаются на волны меньших размеров.

Вследствие нелинейных волн любые параметры среды: (скорость, температура, давление, плотность) могут испытывать хаотические колебания, изменяются от точки к точке и во времени непериодически. Они очень чувствительны к малейшим изменением параметров среды. В турбулентном течении мгновенные параметры среды распределены по случайному закону. Этим турбулентные течения отличаются от ламинарных течений. Но управляя средними параметрами, мы можем управлять турбулентностью. Например, изменяя диаметр трубы, мы управляем числом Рейнольдса, расходом топлива и скоростью заполнения бака ракеты.

Уравнения Навье — Стокса (обычные, а не усреднённые по какому-то интервалу времени) описывают и мягкую, и жёсткую потерю устойчивости течений. Их можно вывести тремя способами из общих законов сохранения: постулируя закон трения Ньютона(обобщённый), следуя методу Чепмена-Энскога и из метода Грэда.

При вязкости равной нулю уравнения сводятся к уравнению Эйлера. Точные решения уравнения Эйлера также хаотичны.

Общепринято считать проекцию вектора скорости на ось координат в турбулентном потоке, состоящей из средней или осредненной величины, за некоторое выбранное время, и плюс мгновенной составляющей:

U = Ucp + u' = 100 м/c + 0.5 м/с.

Здесь u' — пульсационная составляющая или пульсация. Удобно оказалось ввести степень турбулентности:

e = 100 %*u'/Ucp = 100 %*0.5/100 = 0,5 %.

Для трех осей: e = (u' + v' + w')/Ucp.

Турбуленое течение с большим числом Рейнольдса называют развитой турбулентностью. При разных граничных условиях оно всегда приводит к созданию одного и того же профиля скоростей. Это свойство независимости параметров от числа Рейнольдса называют автомодельностью течения. Наблюдается экспериментально в струях или в пограничном слое.

Можно создать изотропную турбулентность, когда статистические параметры течения (функция распределения вероятности, дисперсия, моменты) одинаковы в направлении разных осей координат и не зависят от времени.

Теория однородной турбулентности (то есть, при очень больших числах Рейнольдса, когда ее статистические параметры не зависят от времени и примерно постоянны в течении, но зависят от направления) была создана советскими учёными Обуховым и Колмогоровым. И использовалась затем во многих инженерных расчётах. Теория привела к созданию упрощённых полуэмпирических моделей течения: k-ε (ка-эпсилон) и многих других.

Большинство течений жидкостей и газов в природе (движение воздуха в земной атмосфере, воды в реках и морях, газа в атмосферах Солнца и звёзд и в межзвёздных туманностях и т. п.), в технических устройствах (в трубах, каналах, струях, в пограничных слоях около движущихся в жидкости или газе твёрдых тел, в следах за такими телами и т. п.) турбулентны из-за наличия источников энергии и импульса, наличия внешних возмущающих сил или отсутствия сил сопротивления трения в квантовых жидкостях.

При процессах горения или химических реакциях на явление турбулентности накладываются множество других физических и химических процессов. Например, эффект конвекции, автоколебаний, гистерезиса. В этом случае говорят о турбулентной конвекции. Обычно принимается, что переход от ламинарного течения к турбулентному происходит при достижении критического числа Рейнольдса (Re). Критическое значение числа Рейнольдса зависит от конкретного вида течения, его коэффициента вязкости, который зависит от температуры, которое зависит от давления (течение в круглой трубе, обтекание шара и т. п.). Например, для течения в круглой трубе $ Re_{kp} \simeq 2300 $. В последнее время показано, что это правомерно только для напорных потоков. Но удар по трубе, её резкое вращение или колебание могут вызвать появление турбулентности.

То есть, турбулентность может возникать самопроизвольно, а может в результате действий нескольких внешних сил.

При изучении течения жидкости через трубки малого диаметра французским врачом и учёным Пуазейлем в 1840—1842 гг. выведена формула, по которой можно рассчитать расход воды через трубу.[1][2] До Пуазейля исследованием движения вязкой жидкости через трубы малого диаметра занимался Хаген (1797—1884). При большом расходе формула оказалась неверной. Причина в том, что в трубе возникала турбулентность.

Стоксом, английским учёным-теоретиком были найдены решения уравнения движения вязкой жидкости для малых чисел Re (это второй закон Ньютона с добавками сил давления и сил вязкости), которые он вывел в 1845 г. для движения жидкости в круглой трубе. Затем он получил формулу силы сопротивления при равномерном движении шара в неограниченной жидкости в 1851 году. Её стали использовать для определения коэффициента динамической вязкости. Но решения совпали с опытом лишь при малых скоростях движения жидкости и диаметрах трубы и шара.

Причина этого расхождения была объяснена только опытами Рейнольдса в 1883 г. Он показал существование двух различных режимов движения жидкости — ламинарного и турбулентного — и нашёл один параметр — число Рейнольдса — который позволил предсказать, наличие турбулентности для данного течения в трубе. Если бы Стокс нашёл точные решения Навье-Стокса, он бы обнаружил турбулентность теоретически.

Это позволило Рейнольдсу в 1883 г. ввести положение, что течения одинакового типа (труба должна быть геометрически подобной) с одинаковым числом Рейнольдса подобны. Этот закон был назван законом подобия. Затем, на основе опытов, стала развиваться теория размерности и подобия.

Так как Хаген не знал, как выглядят уравнения Навье-Стокса, что такое число подобия Рейнольдса, то нельзя говорить, что он или Леонардо да Винчи открыл турбулентность. Они наблюдали хаотическое движение в воде. Но описать количественно, предсказать его наступление не могли. А подобие течения, рождение самоподобных структур, например вихрей, которые сами состоят из таких же вихрей — основное свойство турбулентности.

То есть Рейнольдс как бы открыл то, что уравнение для силы гравитации и закон Кулона подобны с разницей только в коэффициенте. А Хаген и Пуазейль только нашли отдельные параметры, которые входят в точное решение уравнения Навье-Стокса и влияют на течение.

Частичное описание развитой турбулентности в рамках математики XIX века предложил Л. Ричардсон в начале XX века. Мешая ложкой чай в стакане, мы создаем вихри размером порядка размера стакана, ложки. Вязкость действует на течение тем сильнее, чем меньше характерный размер течения. Под характерным размером понимают какой-то геометрический параметр, сильно влияющий на течение. Диаметр стакана, его высота, ширина ложки. При большом числе Рейнольдса на эти крупномасштабные движения молекулярная вязкость действует слабо.

Уравнение движения жидкости (Навье-Стокса) нелинейно, так как скорость жидкости переносится самой скоростью и эти вихри неустойчивы. Они дробятся на более мелкие вихри, те на более мелкие. В конце концов на малых размерах вступает в действие молекулярная вязкость, и самые мелкие вихри затухают за счёт неё. Эта представление назвали прямой каскад (или переход от больших масштабов в меньшие).

Турбулентность формально связана с биологическими объектами, с процессами митоза и роста некоторых раковых опухолей, с теорией радиоактивного распада, с процессами, происходящими на рынках акций.

Есть разница между понятием турбулентность и турбулентное течение. Термин турбулентное течение возник в гидравлике. Затем были открыты квантовые жидкости. Их вязкость всегда равна нулю. Если подсчитать для них число Рейнольдса, оно всегда равно бесконечности, когда проекция вектора скорости не равна нулю. Само турбулентное течение может присутствовать в системе очень мелких вихрей, в некоторых малых частях среды. Поэтому, средняя скорость течения равна нулю, когда квантовая жидкость покоится в сосуде. Число Рейнольдса не определено (в числителе нулевая скорость, в знаменателе нулевая вязкость).

В советской науке Править

До 1917 года в российской науке пользовались термином беспорядочное течение. В 1938 году Капицей было открыто турбулентное течение в квантовых средах — сверхтекучем гелии. В жидком гелии есть два типа звука — первый и второй, они могут создавать волновую турбулентность на его поверхности.

В 1942 году А. Н. Колмогоровым и A. М. Обуховым создана теория однородной турбулентности для несжимаемых течений при больших числах Re. Затем в 60-е годы было начато изучение нелинейных волн, солитонов.

В 1970-е годы в СССР Захаровым Владимиром Евгеньевичем была изучена слабая или «волновая» турбулентность волн на поверхности воды (её называют вырожденной). Турбулентность внутри сред назвали сильной.

В 1975 году введено понятие фрактал математиком Бенуа Мандельбротом. А константа Фейгенбаума, используемая при описании фрактальной среды с детерминированным хаосом, была получена в 1978. Тогда же был открыт сценарий Фейгенбаума (или субгармонический каскад) — частный вид перехода к турбулентности.

Физикам было непонятно, почему при хаотическом движении, похожее на Броуновское, в жидкости или газе вдруг миллиарды молекул сворачиваются в кольцо. В начале 80 годов Ю. Л. Климонтович, профессор МГУ им. Ломоносова выдвинул гипотезу о том, что турбулентность — это не хаотичное, а высокоорганизованное, упорядоченное течение. И что энтропия при переходе от ламинарного к турбулентному течению уменьшается. Поэтому спонтанно образуются различные структуры. Он предложил свой критерий, на основе «S-теоремы» по которому можно было рассчитать степень упорядоченности сплошной среды, используя величину производства энтропии. Он не знал, что сценарий Фейгенбаума и другие их виды встречаются в реальных турбулентных средах и считал, что модели сплошной среды недостаточно для появления турбулентности. И значит в уравнении Навье-Стокса нет турбулентности. Поэтому даже для простого движения воды он вводил в уравнения некие искусственные дополнительные флуктуационные члены, что было ошибкой. Аналогично вводил дополнительные члены в уравнения сохранения импульса или движения О. Рейнольдс.

Его «S-теорема» была очень плохо изложена для экспериментаторов и было не понятно, как её применять в эксперименте и чем она лучше понятия K-энтропии. Она противоречила многолетней практике инженеров. Они часто использовали подход, когда энтропия была постоянной для течения (модель изэнтропического газа).

Турбулентность в природе Править

Животные умеют пользоваться турбулентностью. Обычно они подавляют её и управляют её структурой, умеют извлекать энергию из набегающего потока (или ждут попутного ветра). Например, у них очень гладкая кожа. Форма поверхности тела такова, что её кривизна — гладкая функция. То есть, ваше изображение в зеркале, изготовленном в виде тела дельфина будет плавно, без изломов меняться на большей части поверхности. Площадь, где кривизна претерпевает разрывы, минимальна. Они используют слизь на коже или перья, шерсть для разрушения поверхностных волн, которые потребляют много энергии, когда образуются при взмахе крыла или движении хвоста. Кончик крыла или плавника всегда острый, чтобы размер волны, образовывающейся на конце был минимальный. У китов есть канавки проходящие вдоль тела от рта, создающие особую структуру турбулентного течения.

Мухи (за счёт волосков на теле), бабочки (под микроскопом видны системы на крыльях, как решетки чешуек) и птицы используют машущий полет. Они создают вихри в полете, которые позволяют им создавать в разы большую подъемную силу, чем планер того же веса и развивать большую скорость, тратя меньше энергии.

Турбулентность в технике Править

Её стараются либо подавить, либо искусственно создать. Например, при строительстве Норильского комбината было обнаружено, что малый диаметр труб, в котором течение турбулентно, не приводит к увеличению расхода подаваемого воздуха в доменную печь при увеличении внешнего давления подаваемого воздуха. Поэтому были вынуждены поставить параллелно ещё одну трубу, подающую воздух.

У самолётов ставят винглеты — загнутые кверху законцовки крыла. Они экономят до 4 процентов топлива, так как при этом уменьшается размер и число образуемых за крылом вихрей, которые уносят с собой полезную кинетическую энергию (это так называемые волновые потери).

В тех случаях, когда возникает переходный режим от ламинарного к турбулентному, могут возникать колебания давления, подъемной силы. Поэтому по всей длине крыла ставят вихрегенераторы (изогнутые скобы). Они стабилизируют параметры потока. Течение после них всегда турбулентно. Поэтому подьемная сила крыла постепенно растет с увеличением скорости самолета.

Когда нужно быстро перемешать топливо с воздухом и сжечь его, ставят специальные устройства: центробежные и струйные форсунки в камере сгорания. Они, как и выбранная длина камеры сгорания обеспечивают полное сгорание топлива.

Виды турбулентности Править

• Оптическая турбулентность. Очень мощный луч лазера проходит через стекло и начинает рассеиваться хаотически, сам на себе. Свет — это волны, поэтому это турбулентность световых волн. Хаотичное мерцание звёзд на ночном небе связано с случайным изменением плотности воздуха. Это так же проявление турбулентности.
• Речная турбулентность. Течение воды в реке турбулентно. Но за сотни тысяч лет русло реки может не менять свою форму. Когда число Рейнольдса и расход меняется, река меняет шероховатость своего дна. Река — одна из самых совершенных самоуправляющихся систем в неорганическом мире.
• В жидких кристаллах (нематиках), когда скорость среды равна нулю, наблюдается так называемая «медленная» турбулентность.
• Химическая турбулентность. В частном случае, она может быть описана уравнением В. Н. Николаевского.[3].
• Кварк-глюонная плазма, которая существовала на ранней стадии Вселенной, описывается моделью идеальной жидкости (то есть уравнением Навье-Стокса с величиной вязкости, равной нулю). Это пример турбулентного состояния плазмы.
• Однородная и изотропная
  • Изотропная — когда её статистические параметры не зависят от направления. Создается искусственно на некотором расстоянии после металлической сетки или решетки.
  • Однородная — когда её параметры меняются вдоль выбранной оси, но в данном сечении (например, трубы́) они одинаковы.
• На поверхности вибрирующейся многофазной жидкости. Например в слое стеклянных сфер в кукурузном крахмальном сиропе при частоте 120 Гц и виброускорении в 25 g.

http://chaos.utexas.edu/research/vibrated_cornstarch.htm

• Reynods O., An experimental investigation of the circumstances which determine whether the motion of water shall be direct or sinuous, and of the law of resistance in parallel channels. Phil. Trans. Roy. Soc., London, 1883, v.174
• Feigenbaum M., Journal Stat Physics, 1978, v.19, p. 25
• Feigenbaum M., Journal Stat Physics, 1979, v.21, p. 669
• Фейгенбаум M., Успехи Физических наук, 1983, т.141, с. 343 [перевод Los Alamos Science,1980,v.1, p. 4]
• Ландау Л.Д, Лифшиц Е. М. Гидромеханика , — М.: Наука, 1986. — 736 с.
• Монин А. С., Яглом А. М., Статистическая гидромеханика. В 2-х ч. — Санкт-Петербург: Гидрометеоиздат , Ч. 1, 1992. — 695 с;, Москва, Наука Ч. 2, 1967. — 720 с.
• Обухов А. М. Турбулентность и динамика атмосферы «Гидрометеоиздат» 414 стр. 1988 ISBN 5-286-00059-2
• Проблемы турбулентности. Сборник переводных статей под ред. М. А. Великанова и Н. Т. Швейковского. М.-Л., ОНТИ, 1936. — 332 с.
• Д. И. Гринвальд, В. И. Никора, «Речная турбулентность», Л.,Гидрометеоиздат, 1988,152 с.
• П. Г. Фрик. Турбулентность: модели и подходы. Курс лекций. Часть I. ПГТУ, Пермь, 1998. — 108 с. Часть II. — 136 с.
• П. Берже, И. Помо, К. Видаль, Порядок в хаосе, О детерминистическом подходе к турбулентности, М, Мир, 1991, 368 с.
• K.E. Gustafson, Introduction to partial differential equations and Hilbert space methods — 3rd ed.,1999
• Introducing Fractal Geometry, Nigel Lesmoir Gordon, Will Rood, Ralph Edney, Icon Books,Totem Books, 2000, 176 p.
• Д. Глейк, Хаос, Создание новой науки, 1988,Penguin books, 354 с (написана журналистом для школьников и студентов)
• Ю. Л. Климонтович, Статистическая теория открытых систем, Москва, ТОО Янус, 1995. −624 с.
• Recent Advances in Engineering Science (Springer — Verlag, Berlin. 1989), V. N. Nikolaevskii.
• http://www.lehigh.edu/~jdg4/publications/Ext_Chaos.pdf
• Dan Tanaka, Chemical turbulence equivalent to Nikolavskii turbulence, PHYSICAL REVIEW E 70, 015202(R), 2004
• Г. Голдстейн, Классическая механика,Кембридж, 1950, 408 с.

cs:Turbulentní proudění da:Turbulens de:Turbulenz en:Turbulence es:Turbulencia fi:Turbulenssi fr:Turbulence gl:Turbulencia hr:Turbulencija it:Regime turbolento ja:乱流 lt:Turbulencija lv:Turbulence ms:Gelora nl:Turbulente stroming pl:Turbulencja pt:Turbulência sk:Turbulencia sl:Turbulentni tok su:Galura sv:Turbulens zh:湍流

ru.science.wikia.com

4. Турбулентное течение жидкости

ТУРБУЛЕНТНЫМ называется течение, сопровождающееся интенсивным перемешиванием жидкости с пульсациями скоростей и давлений. Нарядус основным продольным перемещением жидкости наблюдаются поперечные перемещения и вращательные движения отдельных объемов жидкости.

Турбулентное течение жидкости наблюдаются при определенных условиях (при достаточно больших числах Рейнольдса) в трубах, каналах, пограничных слоях около поверхностей движущихся относительно жидкости или газа твёрдых тел, в следах за такими телами, струях, зонах перемешивания между потоками разной скорости, а также в разнообразных природных условиях.

Т. т. отличаются от ламинарных не только характером движения частиц, но также распределением осреднённой скорости по сечению потока, зависимостью средней или макс. скорости, расхода и коэф. сопротивления от числа Рейнольдса Re, гораздо большей интенсивностью тепломассообмена. Профиль осреднённой скорости Т. т. в трубах и каналах отличается от параболич. профиля ламинарных течений меньшей кривизной у оси и более быстрым возрастанием скорости у стенок.

Потери напора при турбулентном движении жидкости

Все гидравлические потери энергии делятся на два типа: потери на трение по длине трубопроводов и местные потери, вызванные такими элементами трубопроводов, в которых вследствие изменения размеров или конфигурации русла происходит изменение скорости потока, отрыв потока от стенок русла и возникновение вихреобразования.

Простейшие местные гидравлические сопротивления можно разделить на расширения, сужения и повороты русла, каждое из которых может быть внезапным или постепенным. Более сложные случаи местного сопротивления представляют собой соединения или комбинации перечисленных простейших сопротивлений.

При турбулентном режиме движения жидкости в трубах эпюра распределения скоростей имеет вид, показанный на рис. В тонком пристенном слое толщиной δ жидкость течет в ламинарном режиме, а остальные слои текут в турбулентном режиме, и называются турбулентным ядром. Таким образом, строго говоря, турбулентного движения в чистом виде не существует. Оно сопровождается ламинарным движением у стенок, хотя слой δ с ламинарным режимом весьма мал по сравнению с турбулентным ядром.

Модель турбулентного режима движения жидкости

Основной расчетной формулой для потерь напора при турбулентном течении жидкости в круглых трубах является уже приводившаяся выше эмпирическая формула, называемая формулой Вейсбаха-Дарси и имеющая следующий вид: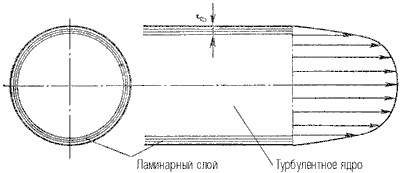

.

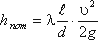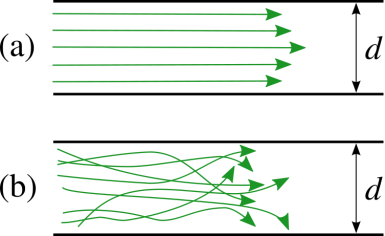
Различие заключается лишь в значениях коэффициента гидравлического трения λ. Этот коэффициент зависит от числа Рейнольдса Re и от безразмерного геометрического фактора - относительной шероховатости Δ/d (или Δ/r0, где r0- радиус трубы).

Критическое число Рейнольдса

Число Рейнольдса, при котором происходит переход от одного режима движения жидкости в другой режим, называется критическим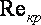. При числе Рейнольдса наблюдается ламинарный режим движения, при числе Рейнольдса - турбулентный режим движения жидкости. Чаще критическое значение числа принимают равным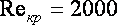, это значение соответствует переходу движения жидкости от турбулентного режима к ламинарного. При переходе от ламинарного режима движения жидкости к турбулентному критическое значение 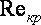имеет большее значение. Критическое значение числа Рейнольдса увеличивается в трубах, сужаются, и уменьшается в тех, что расширяются. Это объясняется тем, что при сужении поперечного сечения скорость движения частиц увеличивается, поэтому тенденция к поперечного перемещения уменьшается.

Таким образом, критерий подобия Рейнольдса позволяет судить о режиме течения жидкости в трубе. При Re < Reкртечение является ламинарным, а при Re > Reкртечение является турбулентным. Точнее говоря, вполне развитое турбулентное течение в трубах устанавливается лишь при Re примерно равно 4000, а при Re = 2300…4000 имеет место переходная, критическая область.



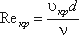
Как показывает опыт, для труб круглого сечения Reкрпримерно равно 2300.

Режим движения жидкости напрямую влияет на степень гидравлического сопротивления трубо-проводов.



Для ламинарного режима

Для турбулентного режима

studfiles.net

Турбуленция - это... Что такое Турбуленция?



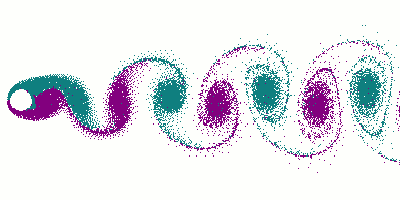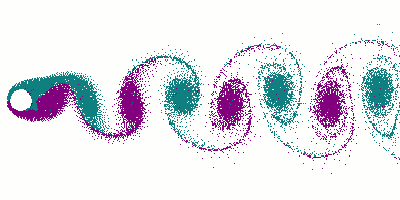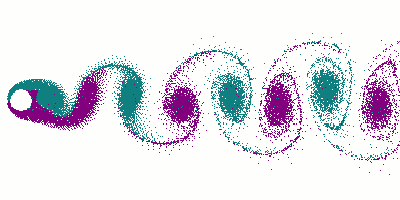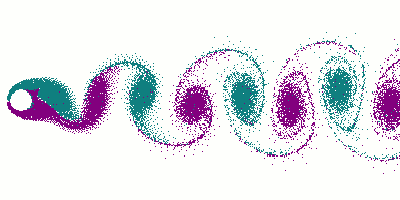
Вихревая дорожка при обтекании цилиндра

Ламинарное (на переднем плане) и турбулентное течение вокруг субмарины

Турбуле́нтность, устар.

турбуле́нция (лат. turbulentus — бурный, беспорядочный), турбуле́нтное тече́ние — явление, заключается в том, что при увеличении интенсивности течения жидкости или газа в среде самопроизвольно образуются многочисленные нелинейные фрактальные волны и обычные, линейные различных размеров, без наличия внешних, случайных, возмущающих среду сил и/или при их присутствии. Для расчёта подобных течений были созданы различные модели турбулентности.

Турбулентность экспериментально открыта английским инженером Рейнольдсом в 1883 году при изучении течения несжимаемой воды в трубах.

В гражданской авиации вхождение в зону высокой турбулентности называют воздушной ямой.

Мгновенные параметры потока (скорость, температура, давление, концентрация примесей) при этом хаотично колеблются вокруг средних значений. Зависимость квадрата амплитуды от частоты колебаний (или спектр Фурье) является непрерывной функцией.

Для возникновения турбулентности необходима сплошная среда, которая подчиняется кинетическому уравнению Больцмана или Навье-Стокса или пограничного слоя. Уравнение Навье-Стокса (в него входит и уравнение сохранения массы или уравнение неразрывности) описывает множество турбулентных течений с достаточной для практики точностью.

Обычно турбулентность наступает при превышении некоторого критического числа Рейнольдса и/или Релея (в частном случае скорости потока при постоянной плотности и диаметре трубы и/или температуры на внешней границе среды).

В частном случае, она наблюдается во многих потоках жидкостей и газов, многофазных течениях, жидких кристаллах, квантовых Бозе- и Ферми- жидкостях, магнитных жидкостях, плазме и любых сплошных средах (например, в песке, земле, металлах). Турбулентность также наблюдается при взрывах звёзд, в сверхтекучем гелии, в нейтронных звёздах, в лёгких человека, движении крови в сердце, при турбулентном (т. н. вибрационном) горении.

Она возникает самопроизвольно, когда соседние области среды следуют рядом или проникают один в другой, при наличии перепада давления или при наличии силы тяжести, или когда области среды обтекают непроницаемые поверхности.

Она может возникать при наличии вынуждающей случайной силы. Обычно внешняя случайная сила и сила тяжести действуют одновременно. Например, при землетрясении или порыве ветра падает лавина с горы, внутри которой течение снега турбулентно.

Турбулентность, например, можно создать:

• увеличив число Рейнольдса (увеличить линейную скорость или угловую скорость вращения потока, размер обтекаемого тела, уменьшить первый или второй коэффициент молекулярной вязкости, увеличить плотность среды) и/или число Релея (нагреть среду) и/или увеличить число Прандтля (уменьшить вязкость).
• и/или задать очень сложный вид внешней силы (примеры: хаотичная сила, удар). Течение может не иметь фрактальных свойств.
• и/или создать сложные граничные и/или начальные условия, задав функцию формы границ. Например, их можно представить случайной функцией. Например: течение при взрыве сосуда с газом. Можно, например, организовать вдув газа в среду, создать шероховатую поверхность. Использовать разгар сопла. Поставить сетку в течение. Течение может при этом не иметь фрактальных свойств.
• и/или создать квантовое состояние. Данное условие применимо только к изотопу гелия 3 и 4. Все остальные вещества замерзают, оставаясь в нормальном, не квантовом состоянии.
• облучить среду звуком высокой интенсивности.
• с помощью химических реакций, например горения. Форма пламени, как и вид водопада может быть хаотичной.

Теория

При больших числах Рейнольдса, скорости потока от небольших изменений на границе зависят слабо. Поэтому при разных начальных скоростях движения корабля формируется одна и та же волна перед его носом, когда он движется с крейсерской скоростью. Нос ракеты обгорает и создаётся одинаковая картина разгара, несмотря на разную начальную скорость.

Фрактальный — означает самоподобный. Например, ваша рука имеет ту же величину фрактальной размерности, как и у ваших предков и потомков. У прямой линии фрактальная размерность равна единице. У плоскости равна двум. У шара трём. Русло реки имеет фрактальную размерность больше 1, но меньше двух, если рассматривать его с высоты спутника. У растений фрактальная размерность вырастает с нуля до величины больше двух. Есть единица измерения геометрических фигур, называется фрактальная размерность. Наш мир нельзя представить в виде множества линий, треугольников, квадратов, сфер и других простейших фигур. И фрактальная размерность позволяет быстро характеризовать геометрические тела сложной формы. Например, у осколка снаряда.

Нелинейная волна — волна, которая обладает нелинейными свойствами. Их амплитуды нельзя складывать при столкновении. Их свойства сильно меняются при малых изменениях параметров. Нелинейные волны называют диссипативными структурами. В них нет линейных процессов дифракции, интерференции, поляризации. Но есть нелинейные процессы, например, самофокусировка. При этом резко, на порядки увеличивается коэффициент диффузии среды, перенос энергии и импульса, сила трения на поверхность.

То есть, в частном случае, в трубе с абсолютно гладкими стенками при скорости выше некоторой критической, в течении любой сплошной среды, температура которой постоянная, под действием только силы тяжести всегда самопроизвольно образуются нелинейные самоподобные волны и затем турбулентность. При этом нет никаких внешних возмущающих сил. Если дополнительно создать возмущающую случайную силу или ямки на внутренней поверхности трубы, то турбулентность также появится.

В частном случае нелинейные волны — вихри, торнадо, солитоны и другие нелинейные явления (например, волны в плазме — обычные и шаровые молнии), происходящие одновременно с линейными процессами (например акустическими волнами).

На математическом языке турбулентность означает, что точное аналитическое решение дифференциальных уравнений в частных производных сохранений импульса и сохранения массы Навье-Стокса (это закон Ньютона с добавлением сил вязкости и сил давления в среде и уравнение неразрывности или сохранения массы) и уравнение энергии представляет собой при превышении некоторого критического числа Рейнольдса, странный аттрактор. Они представляют нелинейные волны и обладают фрактальными, самоподобными свойствами. Но так как волны занимают конечный объем, какая-то часть области течения ламинарно.

При очень малом числе Рейнольса — это всем известные линейные волны на воде небольшой амплитуды. При большой скорости мы наблюдаем нелинейные волны цунами или обрушение волн прибоя. Например, крупные волны за плотиной распадаются на волны меньших размеров.

Вследствие нелинейных волн любые параметры среды: (скорость, температура, давление, плотность) могут испытывать хаотические колебания, изменяются от точки к точке и во времени непериодически. Они очень чувствительны к малейшим изменением параметров среды. В турбулентном течении мгновенные параметры среды распределены по случайному закону. Этим турбулентные течения отличаются от ламинарных течений. Но управляя средними параметрами, мы можем управлять турбулентностью. Например, изменяя диаметр трубы, мы управляем числом Рейнольдса, расходом топлива и скоростью заполнения бака ракеты.

Уравнения Навье — Стокса (обычные, а не усреднённые по какому-то интервалу времени) описывают и мягкую, и жёсткую потерю устойчивости течений. Их можно вывести тремя способами из общих законов сохранения: постулируя закон трения Ньютона(обобщённый), следуя методу Чепмена-Энскога и из метода Грэда.

При вязкости равной нулю уравнения сводятся к уравнению Эйлера. Точные решения уравнения Эйлера также хаотичны.

Общепринято считать проекцию вектора скорости на ось координат в турбулентном потоке, состоящей из средней или осредненной величины, за некоторое выбранное время, и плюс мгновенной составляющей:

U = Ucp + u' = 100 м/c + 0.5 м/с.

Здесь u' — пульсационная составляющая или пульсация. Удобно оказалось ввести степень турбулентности:

e = 100 %*u'/Ucp = 100 %*0.5/100 = 0.5 %.

Для трех осей: e = (u' + v' + w')/Ucp.

Турбуленое течение с большим числом Рейнольдса называют развитой турбулентностью. При разных граничных условиях оно всегда приводит к созданию одного и того же профиля скоростей. Это свойство независимости параметров от числа Рейнольдса называют автомодельностью течения. Наблюдается экспериментально в струях или в пограничном слое.

Можно создать изотропную турбулентность, когда статистические параметры течения (функция распределения вероятности, дисперсия, моменты) одинаковы в направлении разных осей координат и не зависят от времени.

Теория однородной турбулентности (то есть, при очень больших числах Рейнольдса, когда ее статистические параметры не зависят от времени и примерно постоянны в течении, но зависят от направления) была создана советскими учёными Обуховым и Колмогоровым. И использовалась затем во многих инженерных расчётах. Теория привела к созданию упрощённых полуэмпирических моделей течения: k-ε (ка-эпсилон) и многих других.

Большинство течений жидкостей и газов в природе (движение воздуха в земной атмосфере, воды в реках и морях, газа в атмосферах Солнца и звёзд и в межзвёздных туманностях и т. п.), в технических устройствах (в трубах, каналах, струях, в пограничных слоях около движущихся в жидкости или газе твёрдых тел, в следах за такими телами и т. п.) турбулентны из-за наличия источников энергии и импульса, наличия внешних возмущающих сил или отсутствия сил сопротивления трения в квантовых жидкостях.

При процессах горения или химических реакциях на явление турбулентности накладываются множество других физических и химических процессов. Например, эффект конвекции, автоколебаний, гистерезиса. В этом случае говорят о турбулентной конвекции. Обычно принимается, что переход от ламинарного течения к турбулентному происходит при достижении критического числа Рейнольдса (Re). Критическое значение числа Рейнольдса зависит от конкретного вида течения, его коэффициента вязкости, который зависит от температуры, которое зависит от давления (течение в круглой трубе, обтекание шара и т. п.). Например, для течения в круглой трубе 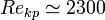. В последнее время показано, что это правомерно только для напорных потоков. Но удар по трубе, ее резкое вращение или колебание могут вызвать появление турбулентности.

То есть, турбулентность может возникать самопроизвольно, а может в результате действий нескольких внешних сил.

При изучении течения жидкости через трубки малого диаметра французским врачом и ученым Пуазейлем в 1840—1842 гг. выведена формула, по которой можно рассчитать расход воды через трубу.[1][2] До Пуазейля исследованием движения вязкой жидкости через трубы малого диаметра занимался Гаген (1710—1769). При большом расходе формула оказалась неверной. Причина в том, что в трубе возникала турбулентность.

Стоксом, английским учёным-теоретиком были найдены решения уравнения движения вязкой жидкости для малых чисел Re (это второй закон Ньютона с добавками сил давления и сил вязкости), которые он вывел в 1845 г. для движения жидкости в круглой трубе. Затем он получил формулу силы сопротивления при равномерном движении шара в неограниченной жидкости в 1851 году. Её стали использовать для определения коэффициента динамической вязкости. Но решения совпали с опытом лишь при малых скоростях движения жидкости и диаметрах трубы и шара.

Причина этого расхождения была объяснена только опытами Рейнольдса в 1883 г. Он показал существование двух различных режимов движения жидкости — ламинарного и турбулентного — и нашёл один параметр — число Рейнольдса — который позволил предсказать, наличие турбулентности для данного течения в трубе. Если бы Стокс нашёл точные решения Навье-Стокса, он бы обнаружил турбулентность теоретически.

Это позволило Рейнольдсу в 1883 г. ввести положение, что течения одинакового типа (труба должна быть геометрически подобной) с одинаковым числом Рейнольдса подобны. Этот закон был назван законом подобия. Затем, на основе опытов, стала развиваться теория размерности и подобия.

Так как Гаген не знал, как выглядят уравнения Навье-Стокса, что такое число подобия Рейнольдса, то нельзя говорить, что он или Леонардо да Винчи открыл турбулентность. Они наблюдали хаотическое движение в воде. Но описать количественно, предсказать его наступление не могли. А подобие течения, рождение самоподобных структур, например вихрей, которые сами состоят из таких же вихрей — основное свойство турбулентности.

То есть Рейнольдс как бы открыл то, что уравнение для силы гравитации и закон Кулона подобны с разницей только в коэффициенте. А Гаген и Пуазейл только нашли отдельные параметры, которые входят в точное решение уравнения Навье-Стокса и влияют на течение.

Частичное описание развитой турбулентности в рамках математики XIX века предложил Л. Ричардсон в начале XX века. Мешая ложкой чай в стакане, мы создаем вихри размером порядка размера стакана, ложки. Вязкость действует на течение тем сильнее, чем меньше характерный размер течения. Под характерным размером понимают какой-то геометрический параметр, сильно влияющий на течение. Диаметр стакана, его высота, ширина ложки. При большом числе Рейнольдса на эти крупномасштабные движения молекулярная вязкость действует слабо.

Уравнение движения жидкости (Навье-Стокса) нелинейно, так как скорость жидкости переносится самой скоростью и эти вихри неустойчивы. Они дробятся на более мелкие вихри, те на более мелкие. В конце концов на малых размерах вступает в действие молекулярная вязкость, и самые мелкие вихри затухают за счёт неё. Эта представление назвали прямой каскад (или переход от больших масштабов в меньшие).

Турбулентность формально связана с биологическими объектами, с процессами митоза и роста некоторых раковых опухолей, с теорией радиоактивного распада, с процессами, происходящими на рынках акций.

Есть разница между понятием турбулентность и турбулентное течение. Термин турбулентное течение возник в гидравлике. Затем были открыты квантовые жидкости. Их вязкость всегда равна нулю. Если подсчитать для них число Рейнольдса, оно всегда равно бесконечности, когда проекция вектора скорости не равна нулю. Само турбулентное течение может присутствовать в системе очень мелких вихрей, в некоторых малых частях среды. Поэтому, средняя скорость течения равна нулю, когда квантовая жидкость покоится в сосуде. Число Рейнольдса не определено (в числителе нулевая скорость, в знаменателе нулевая вязкость).

В советской науке

До 1917 года в российской науке пользовались термином беспорядочное течение. В 1938 году Капицей было открыто турбулентное течение в квантовых средах — сверхтекучем гелии. В жидком гелии есть два типа звука — первый и второй, они могут создавать волновую турбулентность на его поверхности.

В 1942 году А. Н. Колмогоровым и A. М. Обуховым создана теория однородной турбулентности для несжимаемых течений при больших числах Re. Затем в 60-е годы было начато изучение нелинейных волн, солитонов.

В 1970-е годы в СССР Захаровым Владимиром Евгеньевичем была изучена слабая или «волновая» турбулентность волн на поверхности воды (её называют вырожденной). Турбулентность внутри сред назвали сильной.

В 1975 году введено понятие фрактал математиком Бенуа Мандельбротом. А константа Фейгенбаума, используемая при описании фрактальной среды с детерминированным хаосом, была получена в 1978. Тогда же был открыт сценарий Фейгенбаума (или субгармонический каскад) — частный вид перехода к турбулентности.

Физикам было непонятно, почему при хаотическом движении, похожее на Броуновское, в жидкости или газе вдруг миллиарды молекул сворачиваются в кольцо. В начале 80 годов Ю. Л. Климонтович, профессор МГУ им. Ломоносова выдвинул гипотезу о том, что турбулентность — это не хаотичное, а высокоорганизованное, упорядоченное течение. И что энтропия при переходе от ламинарного к турбулентному течению уменьшается. Поэтому спонтанно образуются различные структуры. Он предложил свой критерий, на основе «S-теоремы» по которому можно было рассчитать степень упорядоченности сплошной среды, используя величину производства энтропии. Он не знал, что сценарий Фейгенбаума и другие их виды встречаются в реальных турбулентных средах и считал, что модели сплошной среды недостаточно для появления турбулентности. И значит в уравнении Навье-Стокса нет турбулентности. Поэтому даже для простого движения воды он вводил в уравнения некие искусственные дополнительные флуктуационные члены, что было ошибкой. Аналогично вводил дополнительные члены в уравнения сохранения импульса или движения О. Рейнольдс.

Его «S-теорема» была очень плохо изложена для экспериментаторов и было не понятно, как её применять в эксперименте и чем она лучше понятия K-энтропии. Она противоречила многолетней практике инженеров. Они часто использовали подход, когда энтропия была постоянной для течения (модель изэнтропического газа).

Турбулентность в природе

Животные умеют пользоваться турбулентностью. Обычно они подавляют ее и управляют её структурой, умеют извлекать энергию из набегающего потока (или ждут попутного ветра). Например, у них очень гладкая кожа. Форма поверхности тела такова, что её кривизна — гладкая функция. То есть, ваше изображение в зеркале, изготовленном в виде тела дельфина будет плавно, без изломов меняться на большей части поверхности. Площадь, где кривизна претерпевает разрывы, минимальна. Они используют слизь на коже или перья, шерсть для разрушения поверхностных волн, которые потребляют много энергии, когда образуются при взмахе крыла или движении хвоста. Кончик крыла или плавника всегда острый, чтобы размер волны, образовывающейся на конце был минимальный. У китов есть канавки проходящие вдоль тела от рта, создающие особую структуру турбулентного течения.

Мухи (за счёт волосков на теле), бабочки (под микроскопом видны системы на крыльях, как решетки чешуек) и птицы используют машущий полет. Они создают вихри в полете, которые позволяют им создавать в разы большую подъемную силу, чем планер того же веса и развивать большую скорость, тратя меньше энергии.

Турбулентность в технике

Её стараются либо подавить, либо искуственно создать. Например, при строительстве Норильского комбината было обнаружено, что малый диаметр труб, в котором течение турбулентно, не приводит к увеличению расхода подаваемого воздуха в доменную печь при увеличении внешнего давления подаваемого воздуха. Поэтому были вынуждены поставить параллелно ещё одну трубу, подающую воздух.

У самолётов ставят винглеты — загнутые кверху законцовки крыла. Они экономят до 4 процентов топлива, так как при этом уменьшается размер и число образовываемых за крылом вихрей, которые уносят с собой полезную кинетическую энергию (это так называемые волновые потери).

В тех случаях, когда возникает переходный режим от ламинарного к турбулентному, могут возникать колебания давления, подъемной силы. Поэтому по всей длине крыла ставят вихрегенераторы (изогнутые скобы). Они стабилизируют параметры потока. Течение после них всегда турбулентно. Поэтому подьемная сила крыла постепенно растет с увеличением скорости самолета.

Когда нужно быстро перемешать топливо с воздухом и сжечь его, ставят специальные устройства: центробежные и струйные форсунки в камере сгорания. Они, как и выбранная длина камеры сгорания обеспечивают полное сгорание топлива.

Виды турбулентности

• Оптическая турбулентность. Очень мощный луч лазера проходит через стекло и начинает рассеиваться хаотически, сам на себе. Свет — это волны, поэтому это турбулентность световых волн. Хаотичное мерцание звёзд на ночном небе связано с случайным изменением плотности воздуха. Это так же проявление турбулентности.
• Речная турбулентность. Течение воды в реке турбулентно. Но за сотни тысяч лет русло реки может не менять свою форму. Когда число Рейнольдса и расход меняется, река меняет шероховатость своего дна. Река — одна из самых совершенных самоуправляющихся систем в неорганическом мире.
• В жидких кристаллах (нематиках), когда скорость среды равна нулю, наблюдается так называемая «медленная» турбулентность.
• Химическая турбулентность. В частном случае, она может быть описана уравнением В. Н. Николаевского.[3].
• Кварк-глюонная плазма, которая существовала на ранней стадии Вселенной, описывается моделью идеальной жидкости (то есть уравнением Навье-Стокса с величиной вязкости, равной нулю). Это пример турбулентного состояния плазмы.
• Однородная и изотропная
  • Изотропная — когда её статистические параметры не зависят от направления. Создается искуственно на некотором расстоянии после металлической сетки или решетки.
  • Однородная - когда её параметры меняются вдоль выбранной оси, но в данном сечении (например, трубы́) они одинаковы.
• На поверхности вибрирующейся многофазной жидкости. Например в слое стеклянных сфер в кукурузном крахмальном сиропе при частоте 120 Гц и виброускорении в 25 g.

http://chaos.utexas.edu/research/vibrated_cornstarch.htm

Литература

• Reynods O., An experimental investigation of the circumstances which determine whether the motion of water shall be direct or sinuous, and of the law of resistance in parallel channels. Phil. Trans. Roy. Soc., London, 1883, v.174
• Feigenbaum M., Journal Stat Physics, 1978, v.19, p.25
• Feigenbaum M., Journal Stat Physics, 1979, v.21, p.669
• Фейгенбаум M., Успехи Физических наук, 1983, т.141, с. 343 [перевод Los Alamos Science,1980,v.1, p.4]
• Ландау Л.Д, Лифшиц Е. М. Гидромеханика , — М.: Наука, 1986. — 736 с.
• Монин А. С., Яглом А. М., Статистическая гидромеханика. В 2-х ч. — Санкт-Петербург: Гидрометеоиздат , Ч. 1, 1992. — 695 с;, Москва, Наука Ч. 2, 1967. — 720 с.
• Обухов А. М. Турбулентность и динамика атмосферы «Гидрометеоиздат» 414 стр. 1988 ISBN 5-286-00059-2
• Проблемы турбулентности. Сборник переводных статей под ред. М. А. Великанова и Н. Т. Швейковского. М.-Л., ОНТИ, 1936. — 332 с.
• Д. И. Гринвальд, В. И. Никора, «Речная турбулентность», Л.,Гидрометеоиздат, 1988,152 с.
• П. Г. Фрик. Турбулентность: модели и подходы. Курс лекций. Часть I. ПГТУ, Пермь, 1998. — 108 с. Часть II. — 136 с.
• П. Берже, И. Помо, К. Видаль, Порядок в хаосе, О детерминистическом подходе к турбулентности, М, Мир, 1991, 368 с.
• K.E. Gustafson, Introduction to partial differential equations and Hilbert space methods — 3rd ed.,1999
• Introducing Fractal Geometry, Nigel Lesmoir Gordon, Will Rood, Ralph Edney, Icon Books,Totem Books, 2000, 176 p.
• Д. Глейк, Хаос, Создание новой науки, 1988,Penguin books, 354 с (написана журналистом для школьников и студентов)
• Ю. Л. Климонтович, Статистическая теория открытых систем, Москва, ТОО Янус, 1995. −624 с.
• Recent Advances in Engineering Science (Springer — Verlag, Berlin. 1989), V. N. Nikolaevskii.
• http://www.lehigh.edu/~jdg4/publications/Ext_Chaos.pdf
• Dan Tanaka, Chemical turbulence equivalent to Nikolavskii turbulence, PHYSICAL REVIEW E 70, 015202(R), 2004
• Г. Голдстейн, Классическая механика,Кембридж, 1950, 408 с.

См. также

Примечания

Wikimedia Foundation. 2010.

dic.academic.ru

Турбулентность | Virtual Laboratory Wiki

Файл:Vortex-street-animation.gif Файл:Los Angeles attack sub 2.jpg

Турбуле́нтность, устар. турбуле́нция (лат. turbulentus — бурный, беспорядочный), турбуле́нтное тече́ние — явление, заключается в том, что при увеличении интенсивности течения жидкости или газа в среде самопроизвольно образуются многочисленные нелинейные фрактальные волны и обычные, линейные различных размеров, без наличия внешних, случайных, возмущающих среду сил и/или при их присутствии. Для расчёта подобных течений были созданы различные модели турбулентности.

Турбулентность экспериментально открыта английским инженером Рейнольдсом в 1883 году при изучении течения несжимаемой воды в трубах.

В гражданской авиации вхождение в зону высокой турбулентности называют воздушной ямой.

Мгновенные параметры потока (скорость, температура, давление, концентрация примесей) при этом хаотично колеблются вокруг средних значений. Зависимость квадрата амплитуды от частоты колебаний (или спектр Фурье) является непрерывной функцией.

Для возникновения турбулентности необходима сплошная среда, которая подчиняется кинетическому уравнению Больцмана или Навье-Стокса или пограничного слоя. Уравнение Навье-Стокса (в него входит и уравнение сохранения массы или уравнение неразрывности) описывает множество турбулентных течений с достаточной для практики точностью.

Обычно турбулентность наступает при превышении некоторого критического числа Рейнольдса и/или Релея (в частном случае скорости потока при постоянной плотности и диаметре трубы и/или температуры на внешней границе среды).

В частном случае, она наблюдается во многих потоках жидкостей и газов, многофазных течениях, жидких кристаллах, квантовых Бозе- и Ферми- жидкостях, магнитных жидкостях, плазме и любых сплошных средах (например, в песке, земле, металлах). Турбулентность также наблюдается при взрывах звёзд, в сверхтекучем гелии, в нейтронных звёздах, в лёгких человека, движении крови в сердце, при турбулентном (т. н. вибрационном) горении.

Она возникает самопроизвольно, когда соседние области среды следуют рядом или проникают один в другой, при наличии перепада давления или при наличии силы тяжести, или когда области среды обтекают непроницаемые поверхности.

Она может возникать при наличии вынуждающей случайной силы. Обычно внешняя случайная сила и сила тяжести действуют одновременно. Например, при землетрясении или порыве ветра падает лавина с горы, внутри которой течение снега турбулентно.

Турбулентность, например, можно создать:

• увеличив число Рейнольдса (увеличить линейную скорость или угловую скорость вращения потока, размер обтекаемого тела, уменьшить первый или второй коэффициент молекулярной вязкости, увеличить плотность среды) и/или число Релея (нагреть среду) и/или увеличить число Прандтля (уменьшить вязкость).
• и/или задать очень сложный вид внешней силы (примеры: хаотичная сила, удар). Течение может не иметь фрактальных свойств.
• и/или создать сложные граничные и/или начальные условия, задав функцию формы границ. Например, их можно представить случайной функцией. Например: течение при взрыве сосуда с газом. Можно, например, организовать вдув газа в среду, создать шероховатую поверхность. Использовать разгар сопла. Поставить сетку в течение. Течение может при этом не иметь фрактальных свойств.
• и/или создать квантовое состояние. Данное условие применимо только к изотопу гелия 3 и 4. Все остальные вещества замерзают, оставаясь в нормальном, не квантовом состоянии.
• облучить среду звуком высокой интенсивности.
• с помощью химических реакций, например горения. Форма пламени, как и вид водопада может быть хаотичной.

При больших числах Рейнольдса, скорости потока от небольших изменений на границе зависят слабо. Поэтому при разных начальных скоростях движения корабля формируется одна и та же волна перед его носом, когда он движется с крейсерской скоростью. Нос ракеты обгорает и создаётся одинаковая картина разгара, несмотря на разную начальную скорость.

Фрактальный — означает самоподобный. Например, ваша рука имеет ту же величину фрактальной размерности, как и у ваших предков и потомков. У прямой линии фрактальная размерность равна единице. У плоскости равна двум. У шара трём. Русло реки имеет фрактальную размерность больше 1, но меньше двух, если рассматривать его с высоты спутника. У растений фрактальная размерность вырастает с нуля до величины больше двух. Есть единица измерения геометрических фигур, называется фрактальная размерность. Наш мир нельзя представить в виде множества линий, треугольников, квадратов, сфер и других простейших фигур. И фрактальная размерность позволяет быстро характеризовать геометрические тела сложной формы. Например, у осколка снаряда.

Нелинейная волна — волна, которая обладает нелинейными свойствами. Их амплитуды нельзя складывать при столкновении. Их свойства сильно меняются при малых изменениях параметров. Нелинейные волны называют диссипативными структурами. В них нет линейных процессов дифракции, интерференции, поляризации. Но есть нелинейные процессы, например, самофокусировка. При этом резко, на порядки увеличивается коэффициент диффузии среды, перенос энергии и импульса, сила трения на поверхность.

То есть, в частном случае, в трубе с абсолютно гладкими стенками при скорости выше некоторой критической, в течение любой сплошной среды, температура которой постоянная, под действием только силы тяжести всегда самопроизвольно образуются нелинейные самоподобные волны и затем турбулентность. При этом нет никаких внешних возмущающих сил. Если дополнительно создать возмущающую случайную силу или ямки на внутренней поверхности трубы, то турбулентность также появится.

В частном случае нелинейные волны — вихри, торнадо, солитоны и другие нелинейные явления (например, волны в плазме — обычные и шаровые молнии), происходящие одновременно с линейными процессами (например акустическими волнами).

На математическом языке турбулентность означает, что точное аналитическое решение дифференциальных уравнений в частных производных сохранений импульса и сохранения массы Навье-Стокса (это закон Ньютона с добавлением сил вязкости и сил давления в среде и уравнение неразрывности или сохранения массы) и уравнение энергии представляет собой при превышении некоторого критического числа Рейнольдса, странный аттрактор. Они представляют нелинейные волны и обладают фрактальными, самоподобными свойствами. Но так как волны занимают конечный объём, какая-то часть области течения ламинарно.

При очень малом числе Рейнольса — это всем известные линейные волны на воде небольшой амплитуды. При большой скорости мы наблюдаем нелинейные волны цунами или обрушение волн прибоя. Например, крупные волны за плотиной распадаются на волны меньших размеров.

Вследствие нелинейных волн любые параметры среды: (скорость, температура, давление, плотность) могут испытывать хаотические колебания, изменяются от точки к точке и во времени непериодически. Они очень чувствительны к малейшим изменением параметров среды. В турбулентном течении мгновенные параметры среды распределены по случайному закону. Этим турбулентные течения отличаются от ламинарных течений. Но управляя средними параметрами, мы можем управлять турбулентностью. Например, изменяя диаметр трубы, мы управляем числом Рейнольдса, расходом топлива и скоростью заполнения бака ракеты.

Уравнения Навье — Стокса (обычные, а не усреднённые по какому-то интервалу времени) описывают и мягкую, и жёсткую потерю устойчивости течений. Их можно вывести тремя способами из общих законов сохранения: постулируя закон трения Ньютона(обобщённый), следуя методу Чепмена-Энскога и из метода Грэда.

При вязкости равной нулю уравнения сводятся к уравнению Эйлера. Точные решения уравнения Эйлера также хаотичны.

Общепринято считать проекцию вектора скорости на ось координат в турбулентном потоке, состоящей из средней или осредненной величины, за некоторое выбранное время, и плюс мгновенной составляющей:

U = Ucp + u' = 100 м/c + 0.5 м/с.

Здесь u' — пульсационная составляющая или пульсация. Удобно оказалось ввести степень турбулентности:

e = 100 %*u'/Ucp = 100 %*0.5/100 = 0.5 %.

Для трех осей: e = (u' + v' + w')/Ucp.

Турбуленое течение с большим числом Рейнольдса называют развитой турбулентностью. При разных граничных условиях оно всегда приводит к созданию одного и того же профиля скоростей. Это свойство независимости параметров от числа Рейнольдса называют автомодельностью течения. Наблюдается экспериментально в струях или в пограничном слое.

Можно создать изотропную турбулентность, когда статистические параметры течения (функция распределения вероятности, дисперсия, моменты) одинаковы в направлении разных осей координат и не зависят от времени.

Теория однородной турбулентности (то есть, при очень больших числах Рейнольдса, когда ее статистические параметры не зависят от времени и примерно постоянны в течении, но зависят от направления) была создана советскими учёными Обуховым и Колмогоровым. И использовалась затем во многих инженерных расчётах. Теория привела к созданию упрощённых полуэмпирических моделей течения: k-ε (ка-эпсилон) и многих других.

Большинство течений жидкостей и газов в природе (движение воздуха в земной атмосфере, воды в реках и морях, газа в атмосферах Солнца и звёзд и в межзвёздных туманностях и т. п.), в технических устройствах (в трубах, каналах, струях, в пограничных слоях около движущихся в жидкости или газе твёрдых тел, в следах за такими телами и т. п.) турбулентны из-за наличия источников энергии и импульса, наличия внешних возмущающих сил или отсутствия сил сопротивления трения в квантовых жидкостях.

При процессах горения или химических реакциях на явление турбулентности накладываются множество других физических и химических процессов. Например, эффект конвекции, автоколебаний, гистерезиса. В этом случае говорят о турбулентной конвекции. Обычно принимается, что переход от ламинарного течения к турбулентному происходит при достижении критического числа Рейнольдса (Re). Критическое значение числа Рейнольдса зависит от конкретного вида течения, его коэффициента вязкости, который зависит от температуры, которое зависит от давления (течение в круглой трубе, обтекание шара и т. п.). Например, для течения в круглой трубе $ Re_{kp} \simeq 2300 $. В последнее время показано, что это правомерно только для напорных потоков. Но удар по трубе, её резкое вращение или колебание могут вызвать появление турбулентности.

То есть, турбулентность может возникать самопроизвольно, а может в результате действий нескольких внешних сил.

При изучении течения жидкости через трубки малого диаметра французским врачом и учёным Пуазейлем в 1840—1842 гг. выведена формула, по которой можно рассчитать расход воды через трубу.[1][2] До Пуазейля исследованием движения вязкой жидкости через трубы малого диаметра занимался Гаген (1710—1769). При большом расходе формула оказалась неверной. Причина в том, что в трубе возникала турбулентность.

Стоксом, английским учёным-теоретиком были найдены решения уравнения движения вязкой жидкости для малых чисел Re (это второй закон Ньютона с добавками сил давления и сил вязкости), которые он вывел в 1845 г. для движения жидкости в круглой трубе. Затем он получил формулу силы сопротивления при равномерном движении шара в неограниченной жидкости в 1851 году. Её стали использовать для определения коэффициента динамической вязкости. Но решения совпали с опытом лишь при малых скоростях движения жидкости и диаметрах трубы и шара.

Причина этого расхождения была объяснена только опытами Рейнольдса в 1883 г. Он показал существование двух различных режимов движения жидкости — ламинарного и турбулентного — и нашёл один параметр — число Рейнольдса — который позволил предсказать, наличие турбулентности для данного течения в трубе. Если бы Стокс нашёл точные решения Навье-Стокса, он бы обнаружил турбулентность теоретически.

Это позволило Рейнольдсу в 1883 г. ввести положение, что течения одинакового типа (труба должна быть геометрически подобной) с одинаковым числом Рейнольдса подобны. Этот закон был назван законом подобия. Затем, на основе опытов, стала развиваться теория размерности и подобия.

Так как Гаген не знал, как выглядят уравнения Навье-Стокса, что такое число подобия Рейнольдса, то нельзя говорить, что он или Леонардо да Винчи открыл турбулентность. Они наблюдали хаотическое движение в воде. Но описать количественно, предсказать его наступление не могли. А подобие течения, рождение самоподобных структур, например вихрей, которые сами состоят из таких же вихрей — основное свойство турбулентности.

То есть Рейнольдс как бы открыл то, что уравнение для силы гравитации и закон Кулона подобны с разницей только в коэффициенте. А Гаген и Пуазейл только нашли отдельные параметры, которые входят в точное решение уравнения Навье-Стокса и влияют на течение.

Частичное описание развитой турбулентности в рамках математики XIX века предложил Л. Ричардсон в начале XX века. Мешая ложкой чай в стакане, мы создаем вихри размером порядка размера стакана, ложки. Вязкость действует на течение тем сильнее, чем меньше характерный размер течения. Под характерным размером понимают какой-то геометрический параметр, сильно влияющий на течение. Диаметр стакана, его высота, ширина ложки. При большом числе Рейнольдса на эти крупномасштабные движения молекулярная вязкость действует слабо.

Уравнение движения жидкости (Навье-Стокса) нелинейно, так как скорость жидкости переносится самой скоростью и эти вихри неустойчивы. Они дробятся на более мелкие вихри, те на более мелкие. В конце концов на малых размерах вступает в действие молекулярная вязкость, и самые мелкие вихри затухают за счёт неё. Эта представление назвали прямой каскад (или переход от больших масштабов в меньшие).

Турбулентность формально связана с биологическими объектами, с процессами митоза и роста некоторых раковых опухолей, с теорией радиоактивного распада, с процессами, происходящими на рынках акций.

Есть разница между понятием турбулентность и турбулентное течение. Термин турбулентное течение возник в гидравлике. Затем были открыты квантовые жидкости. Их вязкость всегда равна нулю. Если подсчитать для них число Рейнольдса, оно всегда равно бесконечности, когда проекция вектора скорости не равна нулю. Само турбулентное течение может присутствовать в системе очень мелких вихрей, в некоторых малых частях среды. Поэтому, средняя скорость течения равна нулю, когда квантовая жидкость покоится в сосуде. Число Рейнольдса не определено (в числителе нулевая скорость, в знаменателе нулевая вязкость).

В советской науке Править

До 1917 года в российской науке пользовались термином беспорядочное течение. В 1938 году Капицей было открыто турбулентное течение в квантовых средах — сверхтекучем гелии. В жидком гелии есть два типа звука — первый и второй, они могут создавать волновую турбулентность на его поверхности.

В 1942 году А. Н. Колмогоровым и A. М. Обуховым создана теория однородной турбулентности для несжимаемых течений при больших числах Re. Затем в 60-е годы было начато изучение нелинейных волн, солитонов.

В 1970-е годы в СССР Захаровым Владимиром Евгеньевичем была изучена слабая или «волновая» турбулентность волн на поверхности воды (её называют вырожденной). Турбулентность внутри сред назвали сильной.

В 1975 году введено понятие фрактал математиком Бенуа Мандельбротом. А константа Фейгенбаума, используемая при описании фрактальной среды с детерминированным хаосом, была получена в 1978. Тогда же был открыт сценарий Фейгенбаума (или субгармонический каскад) — частный вид перехода к турбулентности.

Физикам было непонятно, почему при хаотическом движении, похожее на Броуновское, в жидкости или газе вдруг миллиарды молекул сворачиваются в кольцо. В начале 80 годов Ю. Л. Климонтович, профессор МГУ им. Ломоносова выдвинул гипотезу о том, что турбулентность — это не хаотичное, а высокоорганизованное, упорядоченное течение. И что энтропия при переходе от ламинарного к турбулентному течению уменьшается. Поэтому спонтанно образуются различные структуры. Он предложил свой критерий, на основе «S-теоремы» по которому можно было рассчитать степень упорядоченности сплошной среды, используя величину производства энтропии. Он не знал, что сценарий Фейгенбаума и другие их виды встречаются в реальных турбулентных средах и считал, что модели сплошной среды недостаточно для появления турбулентности. И значит в уравнении Навье-Стокса нет турбулентности. Поэтому даже для простого движения воды он вводил в уравнения некие искусственные дополнительные флуктуационные члены, что было ошибкой. Аналогично вводил дополнительные члены в уравнения сохранения импульса или движения О. Рейнольдс.

Его «S-теорема» была очень плохо изложена для экспериментаторов и было не понятно, как её применять в эксперименте и чем она лучше понятия K-энтропии. Она противоречила многолетней практике инженеров. Они часто использовали подход, когда энтропия была постоянной для течения (модель изэнтропического газа).

Турбулентность в природе Править

Животные умеют пользоваться турбулентностью. Обычно они подавляют её и управляют её структурой, умеют извлекать энергию из набегающего потока (или ждут попутного ветра). Например, у них очень гладкая кожа. Форма поверхности тела такова, что её кривизна — гладкая функция. То есть, ваше изображение в зеркале, изготовленном в виде тела дельфина будет плавно, без изломов меняться на большей части поверхности. Площадь, где кривизна претерпевает разрывы, минимальна. Они используют слизь на коже или перья, шерсть для разрушения поверхностных волн, которые потребляют много энергии, когда образуются при взмахе крыла или движении хвоста. Кончик крыла или плавника всегда острый, чтобы размер волны, образовывающейся на конце был минимальный. У китов есть канавки проходящие вдоль тела от рта, создающие особую структуру турбулентного течения.

Мухи (за счёт волосков на теле), бабочки (под микроскопом видны системы на крыльях, как решетки чешуек) и птицы используют машущий полет. Они создают вихри в полете, которые позволяют им создавать в разы большую подъемную силу, чем планер того же веса и развивать большую скорость, тратя меньше энергии.

Турбулентность в технике Править

Её стараются либо подавить, либо искуственно создать. Например, при строительстве Норильского комбината было обнаружено, что малый диаметр труб, в котором течение турбулентно, не приводит к увеличению расхода подаваемого воздуха в доменную печь при увеличении внешнего давления подаваемого воздуха. Поэтому были вынуждены поставить параллелно ещё одну трубу, подающую воздух.

У самолётов ставят винглеты — загнутые кверху законцовки крыла. Они экономят до 4 процентов топлива, так как при этом уменьшается размер и число образовываемых за крылом вихрей, которые уносят с собой полезную кинетическую энергию (это так называемые волновые потери).

В тех случаях, когда возникает переходный режим от ламинарного к турбулентному, могут возникать колебания давления, подъемной силы. Поэтому по всей длине крыла ставят вихрегенераторы (изогнутые скобы). Они стабилизируют параметры потока. Течение после них всегда турбулентно. Поэтому подьемная сила крыла постепенно растет с увеличением скорости самолета.

Когда нужно быстро перемешать топливо с воздухом и сжечь его, ставят специальные устройства: центробежные и струйные форсунки в камере сгорания. Они, как и выбранная длина камеры сгорания обеспечивают полное сгорание топлива.

Виды турбулентности Править

• Оптическая турбулентность. Очень мощный луч лазера проходит через стекло и начинает рассеиваться хаотически, сам на себе. Свет — это волны, поэтому это турбулентность световых волн. Хаотичное мерцание звёзд на ночном небе связано с случайным изменением плотности воздуха. Это так же проявление турбулентности.
• Речная турбулентность. Течение воды в реке турбулентно. Но за сотни тысяч лет русло реки может не менять свою форму. Когда число Рейнольдса и расход меняется, река меняет шероховатость своего дна. Река — одна из самых совершенных самоуправляющихся систем в неорганическом мире.
• В жидких кристаллах (нематиках), когда скорость среды равна нулю, наблюдается так называемая «медленная» турбулентность.
• Химическая турбулентность. В частном случае, она может быть описана уравнением В. Н. Николаевского.[3].
• Кварк-глюонная плазма, которая существовала на ранней стадии Вселенной, описывается моделью идеальной жидкости (то есть уравнением Навье-Стокса с величиной вязкости, равной нулю). Это пример турбулентного состояния плазмы.
• Однородная и изотропная
  • Изотропная — когда её статистические параметры не зависят от направления. Создается искуственно на некотором расстоянии после металлической сетки или решетки.
  • Однородная - когда её параметры меняются вдоль выбранной оси, но в данном сечении (например, трубы́) они одинаковы.
• На поверхности вибрирующейся многофазной жидкости. Например в слое стеклянных сфер в кукурузном крахмальном сиропе при частоте 120 Гц и виброускорении в 25 g.

http://chaos.utexas.edu/research/vibrated_cornstarch.htm

• Reynods O., An experimental investigation of the circumstances which determine whether the motion of water shall be direct or sinuous, and of the law of resistance in parallel channels. Phil. Trans. Roy. Soc., London, 1883, v.174
• Feigenbaum M., Journal Stat Physics, 1978, v.19, p.25
• Feigenbaum M., Journal Stat Physics, 1979, v.21, p.669
• Фейгенбаум M., Успехи Физических наук, 1983, т.141, с. 343 [перевод Los Alamos Science,1980,v.1, p.4]
• Ландау Л.Д, Лифшиц Е. М. Гидромеханика , — М.: Наука, 1986. — 736 с.
• Монин А. С., Яглом А. М., Статистическая гидромеханика. В 2-х ч. — Санкт-Петербург: Гидрометеоиздат , Ч. 1, 1992. — 695 с;, Москва, Наука Ч. 2, 1967. — 720 с.
• Обухов А. М. Турбулентность и динамика атмосферы «Гидрометеоиздат» 414 стр. 1988 ISBN 5-286-00059-2
• Проблемы турбулентности. Сборник переводных статей под ред. М. А. Великанова и Н. Т. Швейковского. М.-Л., ОНТИ, 1936. — 332 с.
• Д. И. Гринвальд, В. И. Никора, «Речная турбулентность», Л.,Гидрометеоиздат, 1988,152 с.
• П. Г. Фрик. Турбулентность: модели и подходы. Курс лекций. Часть I. ПГТУ, Пермь, 1998. — 108 с. Часть II. — 136 с.
• П. Берже, И. Помо, К. Видаль, Порядок в хаосе, О детерминистическом подходе к турбулентности, М, Мир, 1991, 368 с.
• K.E. Gustafson, Introduction to partial differential equations and Hilbert space methods — 3rd ed.,1999
• Introducing Fractal Geometry, Nigel Lesmoir Gordon, Will Rood, Ralph Edney, Icon Books,Totem Books, 2000, 176 p.
• Д. Глейк, Хаос, Создание новой науки, 1988,Penguin books, 354 с (написана журналистом для школьников и студентов)
• Ю. Л. Климонтович, Статистическая теория открытых систем, Москва, ТОО Янус, 1995. −624 с.
• Recent Advances in Engineering Science (Springer — Verlag, Berlin. 1989), V. N. Nikolaevskii.
• http://www.lehigh.edu/~jdg4/publications/Ext_Chaos.pdf
• Dan Tanaka, Chemical turbulence equivalent to Nikolavskii turbulence, PHYSICAL REVIEW E 70, 015202(R), 2004
• Г. Голдстейн, Классическая механика,Кембридж, 1950, 408 с.

Эта страница использует содержимое раздела Википедии на русском языке. Оригинальная статья находится по адресу: Турбулентность. Список первоначальных авторов статьи можно посмотреть в истории правок. Эта статья так же, как и статья, размещённая в Википедии, доступна на условиях CC-BY-SA .

ru.vlab.wikia.com

Турбулентный поток - это... Что такое Турбулентный поток?



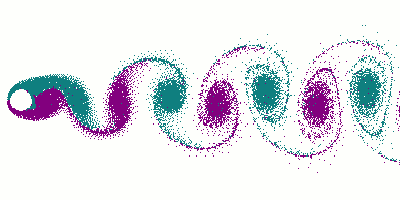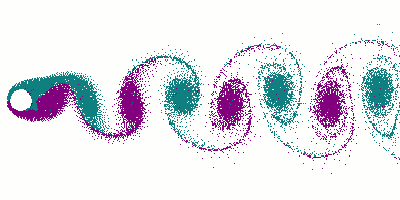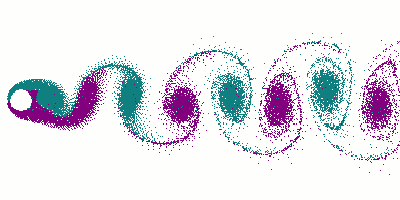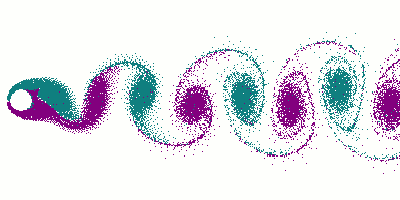
Вихревая дорожка при обтекании цилиндра

Ламинарное (на переднем плане) и турбулентное течение вокруг субмарины

Турбуле́нтность, устар.

турбуле́нция (лат. turbulentus — бурный, беспорядочный), турбуле́нтное тече́ние — явление, заключается в том, что при увеличении интенсивности течения жидкости или газа в среде самопроизвольно образуются многочисленные нелинейные фрактальные волны и обычные, линейные различных размеров, без наличия внешних, случайных, возмущающих среду сил и/или при их присутствии. Для расчёта подобных течений были созданы различные модели турбулентности.

Турбулентность экспериментально открыта английским инженером Рейнольдсом в 1883 году при изучении течения несжимаемой воды в трубах.

В гражданской авиации вхождение в зону высокой турбулентности называют воздушной ямой.

Мгновенные параметры потока (скорость, температура, давление, концентрация примесей) при этом хаотично колеблются вокруг средних значений. Зависимость квадрата амплитуды от частоты колебаний (или спектр Фурье) является непрерывной функцией.

Для возникновения турбулентности необходима сплошная среда, которая подчиняется кинетическому уравнению Больцмана или Навье-Стокса или пограничного слоя. Уравнение Навье-Стокса (в него входит и уравнение сохранения массы или уравнение неразрывности) описывает множество турбулентных течений с достаточной для практики точностью.

Обычно турбулентность наступает при превышении некоторого критического числа Рейнольдса и/или Релея (в частном случае скорости потока при постоянной плотности и диаметре трубы и/или температуры на внешней границе среды).

В частном случае, она наблюдается во многих потоках жидкостей и газов, многофазных течениях, жидких кристаллах, квантовых Бозе- и Ферми- жидкостях, магнитных жидкостях, плазме и любых сплошных средах (например, в песке, земле, металлах). Турбулентность также наблюдается при взрывах звёзд, в сверхтекучем гелии, в нейтронных звёздах, в лёгких человека, движении крови в сердце, при турбулентном (т. н. вибрационном) горении.

Она возникает самопроизвольно, когда соседние области среды следуют рядом или проникают один в другой, при наличии перепада давления или при наличии силы тяжести, или когда области среды обтекают непроницаемые поверхности.

Она может возникать при наличии вынуждающей случайной силы. Обычно внешняя случайная сила и сила тяжести действуют одновременно. Например, при землетрясении или порыве ветра падает лавина с горы, внутри которой течение снега турбулентно.

Турбулентность, например, можно создать:

• увеличив число Рейнольдса (увеличить линейную скорость или угловую скорость вращения потока, размер обтекаемого тела, уменьшить первый или второй коэффициент молекулярной вязкости, увеличить плотность среды) и/или число Релея (нагреть среду) и/или увеличить число Прандтля (уменьшить вязкость).
• и/или задать очень сложный вид внешней силы (примеры: хаотичная сила, удар). Течение может не иметь фрактальных свойств.
• и/или создать сложные граничные и/или начальные условия, задав функцию формы границ. Например, их можно представить случайной функцией. Например: течение при взрыве сосуда с газом. Можно, например, организовать вдув газа в среду, создать шероховатую поверхность. Использовать разгар сопла. Поставить сетку в течение. Течение может при этом не иметь фрактальных свойств.
• и/или создать квантовое состояние. Данное условие применимо только к изотопу гелия 3 и 4. Все остальные вещества замерзают, оставаясь в нормальном, не квантовом состоянии.
• облучить среду звуком высокой интенсивности.
• с помощью химических реакций, например горения. Форма пламени, как и вид водопада может быть хаотичной.

Теория

При больших числах Рейнольдса, скорости потока от небольших изменений на границе зависят слабо. Поэтому при разных начальных скоростях движения корабля формируется одна и та же волна перед его носом, когда он движется с крейсерской скоростью. Нос ракеты обгорает и создаётся одинаковая картина разгара, несмотря на разную начальную скорость.

Фрактальный — означает самоподобный. Например, ваша рука имеет ту же величину фрактальной размерности, как и у ваших предков и потомков. У прямой линии фрактальная размерность равна единице. У плоскости равна двум. У шара трём. Русло реки имеет фрактальную размерность больше 1, но меньше двух, если рассматривать его с высоты спутника. У растений фрактальная размерность вырастает с нуля до величины больше двух. Есть единица измерения геометрических фигур, называется фрактальная размерность. Наш мир нельзя представить в виде множества линий, треугольников, квадратов, сфер и других простейших фигур. И фрактальная размерность позволяет быстро характеризовать геометрические тела сложной формы. Например, у осколка снаряда.

Нелинейная волна — волна, которая обладает нелинейными свойствами. Их амплитуды нельзя складывать при столкновении. Их свойства сильно меняются при малых изменениях параметров. Нелинейные волны называют диссипативными структурами. В них нет линейных процессов дифракции, интерференции, поляризации. Но есть нелинейные процессы, например, самофокусировка. При этом резко, на порядки увеличивается коэффициент диффузии среды, перенос энергии и импульса, сила трения на поверхность.

То есть, в частном случае, в трубе с абсолютно гладкими стенками при скорости выше некоторой критической, в течении любой сплошной среды, температура которой постоянная, под действием только силы тяжести всегда самопроизвольно образуются нелинейные самоподобные волны и затем турбулентность. При этом нет никаких внешних возмущающих сил. Если дополнительно создать возмущающую случайную силу или ямки на внутренней поверхности трубы, то турбулентность также появится.

В частном случае нелинейные волны — вихри, торнадо, солитоны и другие нелинейные явления (например, волны в плазме — обычные и шаровые молнии), происходящие одновременно с линейными процессами (например акустическими волнами).

На математическом языке турбулентность означает, что точное аналитическое решение дифференциальных уравнений в частных производных сохранений импульса и сохранения массы Навье-Стокса (это закон Ньютона с добавлением сил вязкости и сил давления в среде и уравнение неразрывности или сохранения массы) и уравнение энергии представляет собой при превышении некоторого критического числа Рейнольдса, странный аттрактор. Они представляют нелинейные волны и обладают фрактальными, самоподобными свойствами. Но так как волны занимают конечный объем, какая-то часть области течения ламинарно.

При очень малом числе Рейнольса — это всем известные линейные волны на воде небольшой амплитуды. При большой скорости мы наблюдаем нелинейные волны цунами или обрушение волн прибоя. Например, крупные волны за плотиной распадаются на волны меньших размеров.

Вследствие нелинейных волн любые параметры среды: (скорость, температура, давление, плотность) могут испытывать хаотические колебания, изменяются от точки к точке и во времени непериодически. Они очень чувствительны к малейшим изменением параметров среды. В турбулентном течении мгновенные параметры среды распределены по случайному закону. Этим турбулентные течения отличаются от ламинарных течений. Но управляя средними параметрами, мы можем управлять турбулентностью. Например, изменяя диаметр трубы, мы управляем числом Рейнольдса, расходом топлива и скоростью заполнения бака ракеты.

Уравнения Навье — Стокса (обычные, а не усреднённые по какому-то интервалу времени) описывают и мягкую, и жёсткую потерю устойчивости течений. Их можно вывести тремя способами из общих законов сохранения: постулируя закон трения Ньютона(обобщённый), следуя методу Чепмена-Энскога и из метода Грэда.

При вязкости равной нулю уравнения сводятся к уравнению Эйлера. Точные решения уравнения Эйлера также хаотичны.

Общепринято считать проекцию вектора скорости на ось координат в турбулентном потоке, состоящей из средней или осредненной величины, за некоторое выбранное время, и плюс мгновенной составляющей:

U = Ucp + u' = 100 м/c + 0.5 м/с.

Здесь u' — пульсационная составляющая или пульсация. Удобно оказалось ввести степень турбулентности:

e = 100 %*u'/Ucp = 100 %*0.5/100 = 0.5 %.

Для трех осей: e = (u' + v' + w')/Ucp.

Турбуленое течение с большим числом Рейнольдса называют развитой турбулентностью. При разных граничных условиях оно всегда приводит к созданию одного и того же профиля скоростей. Это свойство независимости параметров от числа Рейнольдса называют автомодельностью течения. Наблюдается экспериментально в струях или в пограничном слое.

Можно создать изотропную турбулентность, когда статистические параметры течения (функция распределения вероятности, дисперсия, моменты) одинаковы в направлении разных осей координат и не зависят от времени.

Теория однородной турбулентности (то есть, при очень больших числах Рейнольдса, когда ее статистические параметры не зависят от времени и примерно постоянны в течении, но зависят от направления) была создана советскими учёными Обуховым и Колмогоровым. И использовалась затем во многих инженерных расчётах. Теория привела к созданию упрощённых полуэмпирических моделей течения: k-ε (ка-эпсилон) и многих других.

Большинство течений жидкостей и газов в природе (движение воздуха в земной атмосфере, воды в реках и морях, газа в атмосферах Солнца и звёзд и в межзвёздных туманностях и т. п.), в технических устройствах (в трубах, каналах, струях, в пограничных слоях около движущихся в жидкости или газе твёрдых тел, в следах за такими телами и т. п.) турбулентны из-за наличия источников энергии и импульса, наличия внешних возмущающих сил или отсутствия сил сопротивления трения в квантовых жидкостях.

При процессах горения или химических реакциях на явление турбулентности накладываются множество других физических и химических процессов. Например, эффект конвекции, автоколебаний, гистерезиса. В этом случае говорят о турбулентной конвекции. Обычно принимается, что переход от ламинарного течения к турбулентному происходит при достижении критического числа Рейнольдса (Re). Критическое значение числа Рейнольдса зависит от конкретного вида течения, его коэффициента вязкости, который зависит от температуры, которое зависит от давления (течение в круглой трубе, обтекание шара и т. п.). Например, для течения в круглой трубе 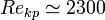. В последнее время показано, что это правомерно только для напорных потоков. Но удар по трубе, ее резкое вращение или колебание могут вызвать появление турбулентности.

То есть, турбулентность может возникать самопроизвольно, а может в результате действий нескольких внешних сил.

При изучении течения жидкости через трубки малого диаметра французским врачом и ученым Пуазейлем в 1840—1842 гг. выведена формула, по которой можно рассчитать расход воды через трубу.[1][2] До Пуазейля исследованием движения вязкой жидкости через трубы малого диаметра занимался Гаген (1710—1769). При большом расходе формула оказалась неверной. Причина в том, что в трубе возникала турбулентность.

Стоксом, английским учёным-теоретиком были найдены решения уравнения движения вязкой жидкости для малых чисел Re (это второй закон Ньютона с добавками сил давления и сил вязкости), которые он вывел в 1845 г. для движения жидкости в круглой трубе. Затем он получил формулу силы сопротивления при равномерном движении шара в неограниченной жидкости в 1851 году. Её стали использовать для определения коэффициента динамической вязкости. Но решения совпали с опытом лишь при малых скоростях движения жидкости и диаметрах трубы и шара.

Причина этого расхождения была объяснена только опытами Рейнольдса в 1883 г. Он показал существование двух различных режимов движения жидкости — ламинарного и турбулентного — и нашёл один параметр — число Рейнольдса — который позволил предсказать, наличие турбулентности для данного течения в трубе. Если бы Стокс нашёл точные решения Навье-Стокса, он бы обнаружил турбулентность теоретически.

Это позволило Рейнольдсу в 1883 г. ввести положение, что течения одинакового типа (труба должна быть геометрически подобной) с одинаковым числом Рейнольдса подобны. Этот закон был назван законом подобия. Затем, на основе опытов, стала развиваться теория размерности и подобия.

Так как Гаген не знал, как выглядят уравнения Навье-Стокса, что такое число подобия Рейнольдса, то нельзя говорить, что он или Леонардо да Винчи открыл турбулентность. Они наблюдали хаотическое движение в воде. Но описать количественно, предсказать его наступление не могли. А подобие течения, рождение самоподобных структур, например вихрей, которые сами состоят из таких же вихрей — основное свойство турбулентности.

То есть Рейнольдс как бы открыл то, что уравнение для силы гравитации и закон Кулона подобны с разницей только в коэффициенте. А Гаген и Пуазейл только нашли отдельные параметры, которые входят в точное решение уравнения Навье-Стокса и влияют на течение.

Частичное описание развитой турбулентности в рамках математики XIX века предложил Л. Ричардсон в начале XX века. Мешая ложкой чай в стакане, мы создаем вихри размером порядка размера стакана, ложки. Вязкость действует на течение тем сильнее, чем меньше характерный размер течения. Под характерным размером понимают какой-то геометрический параметр, сильно влияющий на течение. Диаметр стакана, его высота, ширина ложки. При большом числе Рейнольдса на эти крупномасштабные движения молекулярная вязкость действует слабо.

Уравнение движения жидкости (Навье-Стокса) нелинейно, так как скорость жидкости переносится самой скоростью и эти вихри неустойчивы. Они дробятся на более мелкие вихри, те на более мелкие. В конце концов на малых размерах вступает в действие молекулярная вязкость, и самые мелкие вихри затухают за счёт неё. Эта представление назвали прямой каскад (или переход от больших масштабов в меньшие).

Турбулентность формально связана с биологическими объектами, с процессами митоза и роста некоторых раковых опухолей, с теорией радиоактивного распада, с процессами, происходящими на рынках акций.

Есть разница между понятием турбулентность и турбулентное течение. Термин турбулентное течение возник в гидравлике. Затем были открыты квантовые жидкости. Их вязкость всегда равна нулю. Если подсчитать для них число Рейнольдса, оно всегда равно бесконечности, когда проекция вектора скорости не равна нулю. Само турбулентное течение может присутствовать в системе очень мелких вихрей, в некоторых малых частях среды. Поэтому, средняя скорость течения равна нулю, когда квантовая жидкость покоится в сосуде. Число Рейнольдса не определено (в числителе нулевая скорость, в знаменателе нулевая вязкость).

В советской науке

До 1917 года в российской науке пользовались термином беспорядочное течение. В 1938 году Капицей было открыто турбулентное течение в квантовых средах — сверхтекучем гелии. В жидком гелии есть два типа звука — первый и второй, они могут создавать волновую турбулентность на его поверхности.

В 1942 году А. Н. Колмогоровым и A. М. Обуховым создана теория однородной турбулентности для несжимаемых течений при больших числах Re. Затем в 60-е годы было начато изучение нелинейных волн, солитонов.

В 1970-е годы в СССР Захаровым Владимиром Евгеньевичем была изучена слабая или «волновая» турбулентность волн на поверхности воды (её называют вырожденной). Турбулентность внутри сред назвали сильной.

В 1975 году введено понятие фрактал математиком Бенуа Мандельбротом. А константа Фейгенбаума, используемая при описании фрактальной среды с детерминированным хаосом, была получена в 1978. Тогда же был открыт сценарий Фейгенбаума (или субгармонический каскад) — частный вид перехода к турбулентности.

Физикам было непонятно, почему при хаотическом движении, похожее на Броуновское, в жидкости или газе вдруг миллиарды молекул сворачиваются в кольцо. В начале 80 годов Ю. Л. Климонтович, профессор МГУ им. Ломоносова выдвинул гипотезу о том, что турбулентность — это не хаотичное, а высокоорганизованное, упорядоченное течение. И что энтропия при переходе от ламинарного к турбулентному течению уменьшается. Поэтому спонтанно образуются различные структуры. Он предложил свой критерий, на основе «S-теоремы» по которому можно было рассчитать степень упорядоченности сплошной среды, используя величину производства энтропии. Он не знал, что сценарий Фейгенбаума и другие их виды встречаются в реальных турбулентных средах и считал, что модели сплошной среды недостаточно для появления турбулентности. И значит в уравнении Навье-Стокса нет турбулентности. Поэтому даже для простого движения воды он вводил в уравнения некие искусственные дополнительные флуктуационные члены, что было ошибкой. Аналогично вводил дополнительные члены в уравнения сохранения импульса или движения О. Рейнольдс.

Его «S-теорема» была очень плохо изложена для экспериментаторов и было не понятно, как её применять в эксперименте и чем она лучше понятия K-энтропии. Она противоречила многолетней практике инженеров. Они часто использовали подход, когда энтропия была постоянной для течения (модель изэнтропического газа).

Турбулентность в природе

Животные умеют пользоваться турбулентностью. Обычно они подавляют ее и управляют её структурой, умеют извлекать энергию из набегающего потока (или ждут попутного ветра). Например, у них очень гладкая кожа. Форма поверхности тела такова, что её кривизна — гладкая функция. То есть, ваше изображение в зеркале, изготовленном в виде тела дельфина будет плавно, без изломов меняться на большей части поверхности. Площадь, где кривизна претерпевает разрывы, минимальна. Они используют слизь на коже или перья, шерсть для разрушения поверхностных волн, которые потребляют много энергии, когда образуются при взмахе крыла или движении хвоста. Кончик крыла или плавника всегда острый, чтобы размер волны, образовывающейся на конце был минимальный. У китов есть канавки проходящие вдоль тела от рта, создающие особую структуру турбулентного течения.

Мухи (за счёт волосков на теле), бабочки (под микроскопом видны системы на крыльях, как решетки чешуек) и птицы используют машущий полет. Они создают вихри в полете, которые позволяют им создавать в разы большую подъемную силу, чем планер того же веса и развивать большую скорость, тратя меньше энергии.

Турбулентность в технике

Её стараются либо подавить, либо искуственно создать. Например, при строительстве Норильского комбината было обнаружено, что малый диаметр труб, в котором течение турбулентно, не приводит к увеличению расхода подаваемого воздуха в доменную печь при увеличении внешнего давления подаваемого воздуха. Поэтому были вынуждены поставить параллелно ещё одну трубу, подающую воздух.

У самолётов ставят винглеты — загнутые кверху законцовки крыла. Они экономят до 4 процентов топлива, так как при этом уменьшается размер и число образовываемых за крылом вихрей, которые уносят с собой полезную кинетическую энергию (это так называемые волновые потери).

В тех случаях, когда возникает переходный режим от ламинарного к турбулентному, могут возникать колебания давления, подъемной силы. Поэтому по всей длине крыла ставят вихрегенераторы (изогнутые скобы). Они стабилизируют параметры потока. Течение после них всегда турбулентно. Поэтому подьемная сила крыла постепенно растет с увеличением скорости самолета.

Когда нужно быстро перемешать топливо с воздухом и сжечь его, ставят специальные устройства: центробежные и струйные форсунки в камере сгорания. Они, как и выбранная длина камеры сгорания обеспечивают полное сгорание топлива.

Виды турбулентности

• Оптическая турбулентность. Очень мощный луч лазера проходит через стекло и начинает рассеиваться хаотически, сам на себе. Свет — это волны, поэтому это турбулентность световых волн. Хаотичное мерцание звёзд на ночном небе связано с случайным изменением плотности воздуха. Это так же проявление турбулентности.
• Речная турбулентность. Течение воды в реке турбулентно. Но за сотни тысяч лет русло реки может не менять свою форму. Когда число Рейнольдса и расход меняется, река меняет шероховатость своего дна. Река — одна из самых совершенных самоуправляющихся систем в неорганическом мире.
• В жидких кристаллах (нематиках), когда скорость среды равна нулю, наблюдается так называемая «медленная» турбулентность.
• Химическая турбулентность. В частном случае, она может быть описана уравнением В. Н. Николаевского.[3].
• Кварк-глюонная плазма, которая существовала на ранней стадии Вселенной, описывается моделью идеальной жидкости (то есть уравнением Навье-Стокса с величиной вязкости, равной нулю). Это пример турбулентного состояния плазмы.
• Однородная и изотропная
  • Изотропная — когда её статистические параметры не зависят от направления. Создается искуственно на некотором расстоянии после металлической сетки или решетки.
  • Однородная - когда её параметры меняются вдоль выбранной оси, но в данном сечении (например, трубы́) они одинаковы.
• На поверхности вибрирующейся многофазной жидкости. Например в слое стеклянных сфер в кукурузном крахмальном сиропе при частоте 120 Гц и виброускорении в 25 g.

http://chaos.utexas.edu/research/vibrated_cornstarch.htm

Литература

• Reynods O., An experimental investigation of the circumstances which determine whether the motion of water shall be direct or sinuous, and of the law of resistance in parallel channels. Phil. Trans. Roy. Soc., London, 1883, v.174
• Feigenbaum M., Journal Stat Physics, 1978, v.19, p.25
• Feigenbaum M., Journal Stat Physics, 1979, v.21, p.669
• Фейгенбаум M., Успехи Физических наук, 1983, т.141, с. 343 [перевод Los Alamos Science,1980,v.1, p.4]
• Ландау Л.Д, Лифшиц Е. М. Гидромеханика , — М.: Наука, 1986. — 736 с.
• Монин А. С., Яглом А. М., Статистическая гидромеханика. В 2-х ч. — Санкт-Петербург: Гидрометеоиздат , Ч. 1, 1992. — 695 с;, Москва, Наука Ч. 2, 1967. — 720 с.
• Обухов А. М. Турбулентность и динамика атмосферы «Гидрометеоиздат» 414 стр. 1988 ISBN 5-286-00059-2
• Проблемы турбулентности. Сборник переводных статей под ред. М. А. Великанова и Н. Т. Швейковского. М.-Л., ОНТИ, 1936. — 332 с.
• Д. И. Гринвальд, В. И. Никора, «Речная турбулентность», Л.,Гидрометеоиздат, 1988,152 с.
• П. Г. Фрик. Турбулентность: модели и подходы. Курс лекций. Часть I. ПГТУ, Пермь, 1998. — 108 с. Часть II. — 136 с.
• П. Берже, И. Помо, К. Видаль, Порядок в хаосе, О детерминистическом подходе к турбулентности, М, Мир, 1991, 368 с.
• K.E. Gustafson, Introduction to partial differential equations and Hilbert space methods — 3rd ed.,1999
• Introducing Fractal Geometry, Nigel Lesmoir Gordon, Will Rood, Ralph Edney, Icon Books,Totem Books, 2000, 176 p.
• Д. Глейк, Хаос, Создание новой науки, 1988,Penguin books, 354 с (написана журналистом для школьников и студентов)
• Ю. Л. Климонтович, Статистическая теория открытых систем, Москва, ТОО Янус, 1995. −624 с.
• Recent Advances in Engineering Science (Springer — Verlag, Berlin. 1989), V. N. Nikolaevskii.
• http://www.lehigh.edu/~jdg4/publications/Ext_Chaos.pdf
• Dan Tanaka, Chemical turbulence equivalent to Nikolavskii turbulence, PHYSICAL REVIEW E 70, 015202(R), 2004
• Г. Голдстейн, Классическая механика,Кембридж, 1950, 408 с.

См. также

Примечания

Wikimedia Foundation. 2010.

dic.academic.ru

Турбулентность

Федеральное агентство по образованию

Государственное образовательное учреждение

высшего профессионального образования

московский физико-технический институт

(государственный университет)

Ю.И. Хлопков, В.А. Жаров, С.Л. Горелов

ЛЕКЦИИ ПО ТЕОРЕТИЧЕСКИМ МЕТОДАМ ИССЛЕДОВАНИЯ ТУРБУЛЕНТНОСТИ

Рекомендовано Учебно-методическим объединением

Московского физико-технического института

(государственного университета)

в качестве учебного пособия

для студентов высших учебных заведений

по направлению “Прикладные математика и физика”

Москва 2005

30. 30. Теодорович Э.В. Метод ренормализационной группы в задачах механики // ПММ. – 2004. Т. 68. Вып. 2. С. 335–367.

УДК 532.529

Х58

 

Рецензенты:

Кафедра физики Российского химико-технологического университета

(Зав. кафедрой, доктор физико-математических наук, профессор В.М. Кузнецов)

Доктор физико-математических наук, профессор И.И. Липатов

 

Хлопков Ю.И., Жаров В.А. Горелов С.Л.

Х58 Лекции по теоретическим методам исследования турбу-

лентности: Учебное пособие. — М.: МФТИ, 2005. — 179 с.

ISBN 5-7417-0132-9

Рассмотрены теоретические основы изучения турбулентного движения жидкости. Дан критический анализ многочисленных теоретических подходов описания турбулентности. Турбулентность рассматривается в контексте физических методов. Приведенный в пособии ретроспективный взгляд позволяет легко перейти к изучению современных методов теоретического и численного исследования сложных неоднородных турбулентных течений. Книга доступна как для студентов, так и для аспирантов-аэродинамиков.

Предназначено для широкого круга читателей, интересующихся современными проблемами описания турбулентных течений.

 

УДК 532.529

© Хлопков Ю.И., Жаров В.А., Горелов С.Л., 2005

ISBN 5-7417-0132-9 © Московский физико-технический институт

(государственный университет), 2005

 

ОГЛАВЛЕНИЕ

 

Предисловие . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	4
Современные методы исследования турбулентности . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	12
1. Введение . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	12
2. Турбулентность как естественное состояние жидкости . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	23
3. Турбулентность как ветвь статистической физики . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	56
4. Перенормировочная теория возмущений . . . . . . . . .	107
5. Ренормализационная группа . . . . . . . . . . . . . . . . . . .	143
Заключение . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	161
Список литературы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	170

ПРЕДИСЛОВИЕ

 

Вопросу теоретического описания турбулентных явлений посвящено множество монографий и научных статей, так как эта проблема оказывается неувядающей вот уже в течение более 150 лет. Время от времени появляются очень яркие новые идеи и методы, которые вдохновляют многочисленных исследователей на преодоление необычайных трудностей, связанных с пониманием сути проблемы. Тем не менее практическая важность хотя бы инженерного решения этой проблемы породила огромное число полуэмпирических моделей, в которых вопрос о сути проблемы не ставится, а результаты ориентируются на определенный набор интересных для технических приложений течений. При этом делается упор на описание средних моментов низкого порядка: средняя скорость, среднее давление, средняя кинетическая энергия, средние концентрации химических компонентов и т. п. Кроме того, развивалось моделирование, мотивацией которого была невозможность точного численного описания течений при очень больших числах Рейнольдса.

В последнее время достигнут значительный прогресс в экспериментальном и теоретическом изучении анизотропных турбулентных течений, который позволяет вернуться к исходным проблемам, связанным с существом этого явления [1–4]. Экспериментально обнаружены когерентные структуры, которые представляют существенные элементы течений, оказывающие сильное влияние на различные физические характеристики потоков. Таким образом, течение разбивается на глобально среднее течение, когерентную структуру и стохастический компонент. Были сделаны эксперименты, которые способствовали выявлению деталей когерентных структур. Стохастический же компонент стал теоретически связываться с так называемой фрактальной структурой множества сингулярностей поля завихренности [6–8]. Сингулярная структура турбулентного поля пульсаций следует, например, из простых рассуждений [5].

Рассмотрим уравнение Навье–Стокса:

 

. (1)

 

При n ® 0 уравнение инвариантно относительно преобразований [29]:

 

. (2)

 

Для конечных n уравнение будет инвариантным, если

 

. (3)

 

Заметим, что число Re = VL/n инвариантно относительно преобразований (2) и (3). Предполагая, что мелкомасштабная турбулентность статистически инвариантна относительно этих законов подобия, мы можем выбрать h, исходя из физических соображений. Предположение Колмогорова (1941) – законы подобия турбулентности оставляют неизменным поток энергии в предположении о локальности нелинейных взаимодействий в k-пространстве. Из этого предположения следует, что скорость диссипации энергии инвариантна относительно преобразований подобия (3). По определению, e = ná(Ñv)2ñ, где символ á…ñ – среднее по ансамблю. Отсюда

 

(4)

 

Из инвариантности получаем h = 1/3. Теория Колмогорова имеет сильное продолжение по отношению к величине градиента скорости Ñv. Рассмотрим величину

 

.

Из преобразования подобия с h = 1/3 следует

 

. (5)

 

т.е. градиент скорости является сингулярной величиной.

Сингулярность поля пульсаций с самого начала проблемы обыгрывалась по аналогии с кинетической теорией газов, т.е. несжимаемая жидкость рассматривалась как ансамбль жидких частиц – молей. При этом течение определяется хаотическим движением молей, каждый из которых обладает собственной скоростью и координатой. Изменение характера течения в целом, например, поля средних скоростей происходит из-за турбулентного перемешивания молей с разными собственными скоростями. Вообще любая характеристика течения является усреднением аналогичных характеристик молей, составляющих данный поток. Аналогию между молярным перемешиванием в турбулентном потоке и молекулярным переносом в газах использовали еще Буссинеск и Прандтль для вывода известных формул турбулентного трения. Формула Буссинеска имеет вид

 

,

 

здесь величины l и v – случайные длина перемешивания и пульсационная скорость жидкой частицы. Формула Прандтля имеет вид

 

,

 

здесь L (путь смешения) – эмпирическая величина. В общем случае подобными формулами осуществляется связь двух тензоров: тензора напряжения и тензора скоростей деформации. Заметим, что подобная связь между названными тензорами называется линейной, даже если коэффициент nT зависит от элементов поля скорости.

Большим вкладом в развитие теории турбулентности явилась каскадная теория передачи энергии по спектру турбулентных пульсаций, т. е. передача энергии от больших масштабов к меньшим. Колмогоров и Обухов придали этой теории в однородном и изотропном случае аналитический вид, воспользовавшись теорией размерности и подобия. Результаты были экспериментально подтверждены с большой степенью точности. С тех пор для течений с большими числами Рейнольдса изотропная и однородная турбулентность рассматривается как основная составляющая, хотя и допускается существование ситуаций, в которых спектр энергии еще не установился.

Главный вывод этой теории – наличие инерционной области спектра по волновым числам k: 1/L << k << (1/L)Re3/4, в которой вязкие эффекты диссипации энергии несущественны, благодаря чему спектральная плотность энергии изменя ется в зависимости от волнового числа по закону «–5/3». Включение этого элемента в динамику жидкости приводит к появлению моделей с некоторой феноменологической связью тензора напряжений с тензором скоростей деформаций дополнительными уравнениями, наподобие указанных выше, а также к некоторому числу дополнительных уравнений для величин типа турбулентной энергии, скорости диссипации и т. п. (например, K–e модель). Однако практика показала, что подобные модели имеют узкую область применения. С изменением области применения меняются и константы, входящие в эти уравнения, которые надо снова определять экспериментально. Кроме того, для течений типа пограничного слоя возникали трудности с удовлетворением граничных условий на твердых поверхностях.

Более последовательное, на наш взгляд, направление построения моделей для течений с большими числами Рейнольдса связано с так называемым подсеточным моделированием, смысл которого связан с тем, чтобы оставить в уравнениях гидродинамики только масштабы, превосходящие размеры расчетной сетки (разрешенные масштабы). Это уменьшает количество степеней свободы до разумной величины и позволяет использовать современную вычислительную технику для определения средних полей течения. Размер расчетной сетки выбирают так, чтобы соответствующее ей волновое число находилось в инерционной области, и вводится некоторая связь тензора напряжений с элементами поля течения. Так, например, в модели Смагоринского вводится линейная связь между тензором напряжений и тензором скоростей деформации. Коэффициент вязкости заменяется на коэффициент турбулентной вязкости, который определяется из осреднения подсеточных пульсаций, т. е. пульсаций, размер которых меньше размера сетки. К исходным уравнениям могут быть добавлены несколько дополнительных уравнений, например, для подсеточной кинетической энергии и т. п. Уравнения решаются по времени относительно разрешенных переменных, при этом пульсации с подсеточными частотами отфильтровываются с помощью того или иного фильтра, а то, что остается, усредняется по времени. В этом их главное отличие от моделей типа Буссинеска или Прандтля, которые можно использовать и в стационарных постановках.

Однако практика показала, что сильно анизотропные течения, такие, как течение в пограничном слое или в слое смешения, не ухватываются такими теориями, приводя к неправильному профилю скорости и другим эффектам. Последние экспериментальные достижения показывают, что подобные модели не содержат ряд эффектов, которые наблюдаются в реальных потоках. После скрупулезного анализа оказалось, что подсеточные модели должны содержать эффекты переноса энергии по спектру в инерционной области, включая обратное рассеяние энергии, а также ее перераспределение между нормальными компонентами тензора напряжений. Эти эффекты являются следствием нелинейных взаимодействий и анизотропии. Результаты, полученные при использовании нелинейной модели в крупномасштабном моделировании нейтрального сдвигового пограничного слоя в атмосфере, демонстрируют существенное улучшение в предсказании средних величин по сравнению с линейными моделями типа модели Смагоринского. Эти результаты показывают также сильное влияние модели на структуру течения.

Отметим также методы [24–28], в которых для турбулентного пограничного слоя на основе множественного трехволнового резонанса получены уравнения для пульсаций в виде кинетического уравнения для элементарных волн и явным образом выделенного уравнения для пристеночной когерентной структуры, ответственной за генерацию завихренности со стенки. Явное выделение когерентной структуры позволяет вновь вернуться к стационарной постановке задачи. Характер нелинейности тензора напряжений при этом сохраняется.

Кроме методов подсеточного моделирования большое распространение получили методы статистического моделирования турбулентных течений [16–22]. В этих методах делается попытка феноменологически сформировать уравнение для плотности вероятности флуктуаций поля скорости (и других параметров), которое затем решается с помощью методов Монте-Карло. Такой подход позволяет вычислять как средние моменты низшего порядка, так и более тонкие статистические характеристики. В качестве практических достижений этих подходов можно указать на численное решение задач о турбулентном следе за цилиндром, о расплывании турбулентного пятна, о профиле турбулентного пограничного слоя, обтекание обратной ступеньки и т. п.

Параллельно с указанными результативными подходами к описанию турбулентной динамики развиваются теоретические методы исследования, в которых на основе уравнений Навье–Стокса делаются попытки найти либо статистическое решение проблемы [9, 10] (проблема замыкания, уравнения в функциональных производных), либо используются методы динамических систем (мультифрактальная структура поля завихренности, вейвлетный анализ – фрактальное преобразование свертки) [5–7], либо используются уже зарекомендовавшие себя в исследовании критических явлений ренормгрупповые приложения теоретико-физических асимптотических методов, развитых в применении к описанию динамических систем с бесконечным числом степеней свободы с возбуждением непрерывного спектра масштабов [11–14, 23, 30]. Детали метода громоздки, однако суть некоторых его вариантов можно пояснить на примере метода Гаусса [15] вычисления эллиптического интеграла (в RNG методах тоже вычисляются интегралы для нахождения средних по ансамблю величин, только эти интегралы являются, вообще говоря, континуальными) с помощью арифметико-геометрического среднего. Пусть надо вычислить интеграл вида

 

.

 

Для его вычисления делается преобразование этого интеграла, которое оставляет вид и величину этого выражения неизменными, т. е. новое выражение можно записать как

 

,

 

а m¢ и n¢ определены выражениями

 

,

 

т. е. рекуррентно. Гауссом было доказано, что предел для m¢ и n¢ этих рекуррентных соотношений существует, и m¢ и n¢ совпадают. После этого искомый интеграл I легко выражается через этот предел. Сведение задачи к рекурсивным соотношениям является основой многих RNG подходов.

Далее описаны результаты теоретических исследований, связанных с решением задачи об изотропной и однородной турбулентности. Приводится простое физическое введение в сущность явления, дается краткое описание математических методов, позволяющих описывать системы с бесконечным числом степеней свободы. Кроме того, подводится итог применения этих методов для описания однородной и изотропной турбулентности. Рассмотрены парадоксы и особенности этих методов. Все это дает хорошую основу для понимания и применения современных математических подходов к решению задач о турбулентном движении жидкости.

 

Список литературы

1. 1. Репик Е.У., Соседко Ю.П. Исследование прерывистой структуры течения в пристенной области турбулентного пограничного слоя // Турбулентные течения. – М.: Наука, 1974.

2. 2. Садовский В.С., Синицына Н.П., Таганов Г.И. Численное исследование математической модели пристенного течения в турбулентном пограничном слое // Пристенные турбулентные течения. Ч. 1. – Новосибирск: Изд. СО АН СССР, 1975.

3. 3. Robinson S.K. Coherent Motions in the Turbulent Boundary Layer // Ann. Rev. Fluid Mech. –1991. V. 23. P. 601–639.

4. 4. Хлопков Ю.И., Жаров В.А., Горелов С.Л. Когерентные структуры в турбулентном пограничном слое. – М.: МФТИ, 2002. – 267 с.

5. 5. Benzi R., Paladin G., Parizi G., Vulpiani A. On the multifractal nature of fully developed turbulence and chaotic systems // J. Phys. A. Math. Gen. –1984. 17. P. 3521–3531.

6. 6. Суини Х. и др. Гидродинамические неустойчивости и переход к турбулентности. – М.: Мир, 1984. – 344 с.

7. 7. Farge Maric. Are wavelets and related multiscale techniques useful for turbulence? // Tagungsber. Math. Forschungsinst. Obervolfach. – 1995. N 31. Р. 6–7.

8. 8. Монин А.С., Полубаринова-Кочина П.Я., Хлебников В.И. Космология, гидродинамика, турбулентность. А.А. Фридман и развитие его научного наследия. – М.: Наука, 1989. – 325 с.

9. 9. Монин А.С., Яглом А.М. Статистическая гидромеханика. Теория турбулентности. Т. 2. – М.: 1996. – 742 с.

10. 10. Inoue A. Functional Derivative Equations (including the Hopf equation) in an Analysis on superspace over co-dimentional Frechet-Grassman algebra // Tagungsber. Math. Forschungsinst., Obervolfach. – 1991. N 35. Р. 9.

11. 11. Теодорович Э.В. Использование метода ренормализационной группы // Монин А.С., Яглом А.М. Статистическая гидромеханика. Теория турбулентности. Т. 2. – М.: 1996. – 742 с.

12. 12. Аджемян Л.Ц., Антонов Н.В., Васильев А.Н. Квантовополевая ренормализационная группа в теории развитой турбулентности // УФН. – 1996. Т. 166, № 12. С. 1257–1284.

13. 13. Захаров В.Е., Львов В.С. О статистическом описании нелинейных волновых полей // Известия ВУЗов, Радиофизика. – 1975. Т. XVIII. № 10. С. 1470–1487.

14. 14. Ширков Д.В. Ренормализационная группа, принцип инвариантности и функциональная автомодельность // ДАН СССР. – 1982. Т. 263. С. 64–67.

15. 15. Клайн Ф. Лекции о развитии математики в XIX столетии: в двух томах. Т. 1. – М.: Наука, 1989. – 456 с.

16. 16. Кузнецов В.Р., Сабельников В.А. Турбулентность и горение. – М.: Наука, 1986. – 287 с.

17. 17. Белоцерковский О.М. Численное моделирование в механике сплошных сред. – М.: Физматлит, 1994. – 448 с.

18. 18. Van Slooten P.R., Pope S.B. Advances in PDF modeling for inhomogeneous turbulent flow // Phys. Fluids. – 1998. V. 10, N 1. Р. 246–265.

19. 19. Delarue B.J., Pope S.B. Calculation of subsonic and supersonic turbulent reacting mixing layers using probability density functions methods // Phys. Fluids. – 1998. V. 10, N 2. Р. 487–498.

20. 20. Ong L., Wallace J. M. Joint probability density analysis of the structure and dynamics of the vorticity of a turbulent boundary layer // J. Fluid Mech. – 1998. V. 367. Р. 291–321.

21. 21. Белоцерковский О.М., Иванов С.А., Яницкий В.Е. Прямое статистическое моделирование некоторых задач турбулентности // ЖВМ и МФ. – 1998. Т. 38, № 3. С. 489–503.

22. 22. Белоцерковский О.М., Опарин А.М. Численный эксперимент в турбулентности. От порядка к хаосу. Изд. 2-е, доп. – М.: Наука, 2000. – 223 с.

23. 23. Васильев А.Н. Квантово-полевая ренормгруппа в теории критического поведения и стохастической динамике. Сиб. Изд. ПИАФ, 1998. – 774 с.

24. 24. Жаров В.А., Додонов И.Г., Хлопков Ю.И. Резонансные свойства ламинарного и турбулентного пограничных слоев // Численное моделирование в задачах аэродинамики и экологии. – М.: МФТИ, 1998.

25. 25. Zharov V.A., Dodonov I.G., Khlopkov Yu.I. Resonant properties of laminar and turbulent boundary layers // Proc. of the third seminar on RRDPAE’98, Warsaw University of Technology, Research Bulletin N 7, part II, Warsaw, 1999.

26. 26. Жаров В.А., Додонов И.Г., Хлопков Ю.И. Локализованные когерентные структуры в пограничном слое // ПМТФ.– 2000. Т. 41, № 6. С. 60–68.

27. 27. Bogolepov V.A., Zharov V.A., Lipatov I.I., Khlopkov Yu.I. Turbulent boundary layer model with explicit representation of coherent generative structure // Proc. of Int. conf. «Progress in nonlinear science». Nizhniy Novgorod, Russia, July 2–6, 2001, V. II, pp. 209–214.

28. 28. Жаров В.А., Боголепов В.В., Липатов И.И., Хлопков Ю.И. Модель турбулентного пограничного слоя с явным выделением когерентной генерационной структуры // ПМТФ. 2002. Т. 43, № 4. С. 65–74.

29. 29. Frish U. Fully developed turbulence and singularities // In: Chaotic behavior of deterministic systems, Les Houches, 1981, North-Holland: Amsterdam, 1983, pp. 665–704.

www.o8ode.ru

В чем опасность зоны турбулентности? Что такое маленькая зона турбулентности?

Многие люди не любят пользоваться таким транспортным средством, как самолет. У каждого на этот счет свое мнение, но объединяет их обычно одно. Что? Конечно же, страх. Он может возникнуть по самым разным причинам. Некоторые люди боятся разбиться, другие ненавидят попадать в зоны турбулентности. Кроме того, многие и вовсе считают такой способ передвижения слишком дорогим.

Что такое турбулентность?

И все же есть люди, которые обожают летать. Когда же они попадают в зоны турбулентности, как правило, возникает вопрос о том, вредно ли это. Наслаждаться полетом, чувствовать адреналин при взлете или же посадке - это одно, но когда тело трясет (и не всегда легонько и безопасно), возникают различные доводы и предположения. Итак, что же такое турбулентность и как она сказывается на здоровье человека?

Часто в народе турбулентность называют «болтанкой». Простыми словами, это разного рода колебания самолета, которые возникают в результате вихревых потоков ветра, нисходящих и восходящих. Помимо этого, маленькая зона турбулентности может возникнуть из-за некоторых видов облаков. Как правило, самолет выдерживает такие нагрузки, и пассажиры могут почувствовать лишь небольшое покачивание.

В чем опасность турбулентности?



Каждый пилот заботится о своем самолете и пассажирах. Поэтому он пытается избежать малейшей опасности. Так, пилот избегает зоны облаков. Но бывают случаи, когда самолет попадает в такие потоки воздуха, которые способны бросить его на закритические углы атаки. Как следствие, всё транспортное средство может оказаться под угрозой. Именно поэтому пилот никогда сознательно не полетит в грозовые облака. Такие объекты хорошо видны на локаторе и предупреждают о возможных препятствиях.

Таким образом, зона турбулентности – это не поддающееся прогнозам явление. Оно вызвано скоплением воздушных масс и порой может не отображаться на локаторе пилота. Как следствие, от этого никто не застрахован.

Безопасность прежде всего!

Нельзя точно сказать, опасна ли турбулентность. Все зависит от потоков воздуха. Стоит отметить, что перед началом рейса каждый пилот проходит специальную подготовку. В ходе нее он ознакамливается с погодой и выбирает оптимальный маршрут.

Но также бывают ситуации, когда спланировать или спрогнозировать маршрут невозможно. Когда летишь на самолете больше восьми часов, предугадать изменение погоды просто нереально. Тогда стоит полагаться только на отличные навыки и внимательность пилота. Помимо этого, защитить самолет от неприятностей может специальное оборудование, которое смягчит болтанку.

Другие причины турбулентности

Отметим, что одной из возможных причин образования зоны турбулентности могут стать струйные течения. Их суть заключается в том, что они могут изменяться очень быстро и в разные стороны, то есть в горизонтальном или вертикальном направлениях. Особенностью таких течений является то, что они могут тянуться на несколько сотен тысяч километров. Чаще всего их можно встретить у востока США.

Благодаря плотному трафику в небе самолет может избежать той или иной зоны турбулентности. В иных случаях явление может негативно повлиять на человека и средство передвижения в целом. Очень важно, чтобы попутные самолеты выдерживали определенное расстояние между собой. Во-первых, это необходимо для того, чтобы они не столкнулись, а во-вторых, это помогает уменьшить риск попадания в зону турбулентности.

Многие люди считают, что болтанка возникает в результате ошибки пилота или его непрофессионализма. Это совершенно ошибочное предположение! Самолет очень часто движется на автопилоте, и главная задача командующего – это наблюдать за локаторами в кабинке и за другими приборами. Данная функция отключается в случае сильной тряски, которая возникает при попадании в зону турбулентности. Тогда пилот руководит самолетом вручную. И как сильно будет трясти воздушное судно, зависит только от него самого. Чем больше масса воздушного судна, тем ощутимей будут толчки.

Помимо вышеперечисленных причин, встречается еще и другая. Например, снижаясь, самолет может столкнуться с сильным вихрем, порывом ветра. Но и об этом не стоит слишком беспокоиться, так как в наше время разработаны специальные нормативы и параметры полета в период болтанки, которые позволяют избежать неприятностей. Если они не помогают, тогда в обязанности пилота входит посадить самолет в ближайшем аварийном аэродроме.

Рекомендации пассажирам

Какие бы зоны турбулентности ни встретились на пути у пассажиров, никогда не стоит преждевременно паниковать. Да, не будем отрицать, что такое явление не стоит недооценивать. В лучшем случае перед полетом каждому человеку необходимо немножко подготовиться, прислушавшись к рекомендациям профессионалов и прочитав необходимую литературу.

Но один вопрос все же интересует всех пассажиров: «В чем опасность турбулентности?» Поспешим успокоить всех людей, которые страдают аэрофобией: болтанка может немного напугать, но за 120 лет истории авиации не произошло ни одной катастрофы, причиной которой была бы или могла бы быть турбулентность. Все потому, что пилоты прекрасно знают, как реагировать и вести себя в таких ситуациях. А также сегодня существует масса параметров, нормативов, техник, которые помогают избежать неблагоприятной ситуации.

Турбулентность: опасность или страх?

Причин феноменального явления очень много: завихрение от торцов крыльев, неравномерное прогревание воздуха, встреча воздушных масс, температура которых различается, и многое другое. Но это лишь незначительные факторы, которые могут привести к болтанке. Так или иначе, избежать ее намного легче, чем попасть в эпицентр событий. Будьте уверены, ни один пилот не направит свой самолет в опасное место! Небольшая тряска не должна восприниматься как тревожный знак и угроза для безопасного полета. Вред турбулентности – всего лишь миф, который в условиях развития передовых технологий не может навредить человеку.

fb.ru

---

Смотрите также

• 
  Дозиметры воды
• 
  Вода пирамидальная
• 
  Вода ямаровка
• 
  Медцентр вода
• 
  Воды меривы
• 
  Sulinka вода
• 
  Вода миргород
• 
  Вода сиси
• 
  Пропаналь вода
• 
  Этил вода
• 
  Дефлектор воды