Несжимаемая жидкость. Несжимаемость воды
Несжимаемая жидкость
Рассматривается одномерное движение жидкости в трубе (рис. 3) вдоль оси х. Считая жидкость несжимаемой, принимаем, что в ней невозможно образование пустот, т. е. соблюдается условие неразрывности (сплошности) движения. Исходя из этого, количество жидкости,

Рис. 3.
проходящей в единицу времени через сечения 1—1 (G1x) и 2—2 (G.2x), должно быть одинаково, т. е.
G1x = G2x. (I.12)
Обозначим через  массовую скорость в направлении оси х, где
массовую скорость в направлении оси х, где 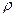 — плотность рассматриваемой жидкости. Так как масса жидкости в рассматриваемом объеме не изменяется, то массовая скорость во всех сечениях будет одна и та же, т. е.
— плотность рассматриваемой жидкости. Так как масса жидкости в рассматриваемом объеме не изменяется, то массовая скорость во всех сечениях будет одна и та же, т. е.
 . (I.13)
. (I.13)
Следовательно,

Формула (1.14) выражает закон сохранения массы при одномерном течении жидкости. Исходя из формулы (1.13)или же (1.14), имеем wx= const, т. е. с учетом постоянства плотности получается  , где и1— средняя скорость в сечении 1—1, а и2— в сечении 2—2.
, где и1— средняя скорость в сечении 1—1, а и2— в сечении 2—2.
При выводе уравнения (1.14) предполагается, что площадь поперечного сечения трубы постоянная. В противном случае, обозначая площадь поперечного сечения 1—1 через F1, а площадь 2—2 — через F2и учитывая, что
 , (I.15)
, (I.15)
из формулы (1.12) получаем
u1F1 = u2F2(I.16)
Из формулы (1.16) видно, что при установившемся течении несжимаемой жидкости средние скорости в поперечных сечениях обратно пропорциональны площадям этих сечений.
Так как при установившемся течении газа массовый расход по длине трубы имеет одно и то же значение, то, исходя из (1.12) и (1.15), для установившегося течения газа получаем
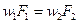
или же
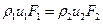 . (I.17)
. (I.17)
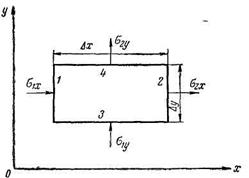
Рис. 4.
Рассмотрим случай плоского течения несжимаемой жидкости. Для этого возьмем параллелепипед со сторонами 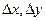 , 1 объемом
, 1 объемом 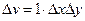 (рис. 4). Количество жидкости, протекающей через стороны 1, 2, 3 и 4 соответственно будет
(рис. 4). Количество жидкости, протекающей через стороны 1, 2, 3 и 4 соответственно будет  ,
,
где wxи wy— массовые скорости в направлениях осей ох и оу. Заметим, что на рис. 4 не ограничиваем направление течения. Жидкость может притекать через грани 1 и 4 и вытекать через грани 2,3 или же притекать через грани 1 и 2 и вытекать через грани 3,4. Также возможны и другие направления течения. Однако количество притекающей жидкости должно быть равно количеству вытекающей жидкости. Это объясняется тем, что рассматриваемая жидкость несжимаемая, т. е. в рассматриваемом объеме масса (плотность) жидкости не изменяется. Если, например, G1x = 7; G2x= 3 и Gl =5, то в силу несжимаемости жидкости со стороны 4 должно вытекать G2y =9. Другими словами,
(G2x-G1x) + (G2y-G1y) = 0. (I.18)
Закон сохранения массы [см. формулу (1.18)] показывает, что количество притекающей в данный объем жидкости равно количеству пмтокающей из него жидкости. Выражения в скобках в формуле (1.18) всегда имеют разные знаки, причем здесь приводятся алгебраические значения G1x,G2x,G1yи G2y. В нашем примере G2y-G1y= 4, а G.2x- G1x=-4. Последнее замечание имеет место при любом варианте течения. Изменение количества жидкости в рассматриваемом прямоугольнике будет:
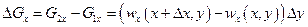 ; (I.19)
; (I.19)
в направлении оси ох и
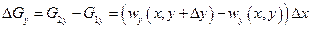 (1.20)
(1.20)
в направлении оси оу.
Во всех случаях течения несжимаемой жидкости AGXи AGyбудут иметь разные знаки и
 . (I.21)
. (I.21)
Формула (1.21) получена с учетом того, что количество притекающей в рассматриваемый объем жидкости равно количеству вытекающей. Подставляя значения 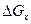 и
и  из (1.19) и (1.20) в (1.21), получаем
из (1.19) и (1.20) в (1.21), получаем
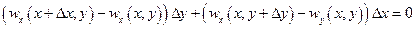 .
.
Разделив последнее выражение на 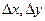 и перейдя к пределу при
и перейдя к пределу при 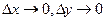 , получим
, получим

Формула (1.22) выражает закон сохранения массы и называется уравнением неразрывности (сплошности) при плоском течении несжимаемой жидкости. В формуле (1.22) 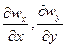 всегда имеют разные знаки. Это объясняется тем, что если, например,
всегда имеют разные знаки. Это объясняется тем, что если, например,  отрицательная величина, то wxубывает, и по направлению ох больше притекает жидкости (через сечение 1), чем вытекает (через сечение 2), что может привести к накоплению жидкости. Поэтому из-за несжимаемости жидкости в направлении оу утечка жидкости должна быть больше ее притока. wyбудет расти вдоль оу, т. е. значение
отрицательная величина, то wxубывает, и по направлению ох больше притекает жидкости (через сечение 1), чем вытекает (через сечение 2), что может привести к накоплению жидкости. Поэтому из-за несжимаемости жидкости в направлении оу утечка жидкости должна быть больше ее притока. wyбудет расти вдоль оу, т. е. значение 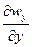 должно быть положительным. Точно также при положительной
должно быть положительным. Точно также при положительной  утечка жидкости в направлении ох должна компенсироваться ее притоком в направлении оу, следовательно wyбудет убывать, т. е, значение
утечка жидкости в направлении ох должна компенсироваться ее притоком в направлении оу, следовательно wyбудет убывать, т. е, значение 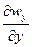 должно быть отрицательным. Наконец, рассмотрим течение несжимаемой жидкости в пространстве. Для этого возьмем параллелепипед (рис. 5), грани которого параллельны координатным плоскостям и имеют площади:
должно быть отрицательным. Наконец, рассмотрим течение несжимаемой жидкости в пространстве. Для этого возьмем параллелепипед (рис. 5), грани которого параллельны координатным плоскостям и имеют площади:
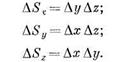
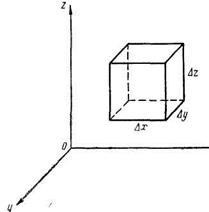
Рис. 5.
Количество жидкости, протекающей через грани взятого параллелепипеда,*определяется по формулам:
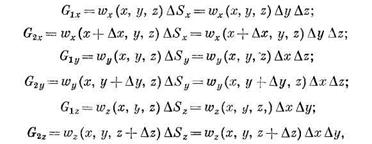
где wz— массовая скорость в направлении оси z.
Изменение количества жидкости в рассматриваемом параллелепипеде будет в направлении осей  :
:
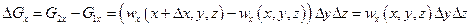
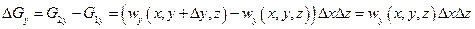
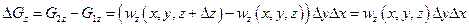
Так как жидкость несжимаемая, то
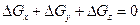 (1.23)
(1.23)
В зависимости от направления движения две из этих величин будут иметь одинаковый знак, а третья величина — противоположный знак. В противном случае жидкость со всех сторон будет притекать в рассматриваемый объем, что физически невозможно из-за несжимаемости жидкости.
Подставив значения 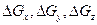 в (1.23), разделив их соответственно на
в (1.23), разделив их соответственно на 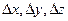 и перейдя соответственно к пределу при
и перейдя соответственно к пределу при 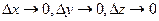 , получим
, получим
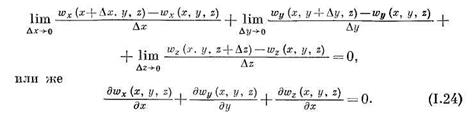
Формула (1-24) выражает закон сохранения массы и называется уравнением неразрывности (сплошности) при пространственном течении несжимаемой жидкости. При получении уравнения (1.24) предполагается, что жидкость несжимаемая, т. е. масса (плотность) жидкости в рассматриваемом объеме не изменяется. Если в (1.24)
значения  ,
, 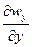 имеют одинаковый знак, например положительный, то это означает, что в направлении ох и оу больше вытекает жидкости, чем притекает, так как в этом случае wxи wyвозрастают. В связи с несжимаемостью жидкости эта утечка должна компенсироваться притоком в направлении oz. По направлению oz приток жидкости в рассматриваемый объем должен быть больше ее утечки из рассматриваемого объема, т. е. wzбудет убывать и,
имеют одинаковый знак, например положительный, то это означает, что в направлении ох и оу больше вытекает жидкости, чем притекает, так как в этом случае wxи wyвозрастают. В связи с несжимаемостью жидкости эта утечка должна компенсироваться притоком в направлении oz. По направлению oz приток жидкости в рассматриваемый объем должен быть больше ее утечки из рассматриваемого объема, т. е. wzбудет убывать и,
следовательно, значение 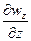 должно быть отрицательным.
должно быть отрицательным.
Сжимаемая жидкость
Если жидкость сжимаемая, т. е. плотность (и, следовательно, масса) жидкости может изменяться во времени, то изменение количества жидкости в рассматриваемом объеме приведет к изменению плотности (массы) жидкости в том же объеме. Так, например, для сжимаемой жидкости (см. рис. 3) 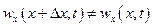 и за некоторый промежуток времени
и за некоторый промежуток времени 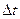 разность, между количествами притока жидкости в данный объем и утечки из него приведет к изменению плотности жидкости в рассматриваемом объеме. При этом если
разность, между количествами притока жидкости в данный объем и утечки из него приведет к изменению плотности жидкости в рассматриваемом объеме. При этом если 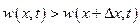 , т. е. в данный объем больше притекает жидкости, чем из него вытекает, то это приведет к увеличению плотности в данном объеме, если же
, т. е. в данный объем больше притекает жидкости, чем из него вытекает, то это приведет к увеличению плотности в данном объеме, если же 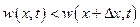 , то количество вытекающей из данного объема жидкости больше количества притекающей в него жидкости, что и приведет к уменьшению плотности жидкости в данном объеме. Таким образом, если в течение некоторого промежутка времени
, то количество вытекающей из данного объема жидкости больше количества притекающей в него жидкости, что и приведет к уменьшению плотности жидкости в данном объеме. Таким образом, если в течение некоторого промежутка времени 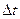 величина
величина 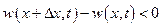 , то плотность в данном объеме возрастает, т. е.
, то плотность в данном объеме возрастает, т. е.
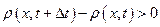 ,
,
если же
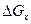
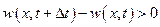 ,
,
то плотность в данном объеме убывает, т. е. 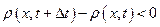 .
.
Следовательно, возрастание массовой скорости w (х, t) в данном объеме за некоторый промежуток времени 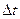 приводит к убыванию плотности жидкости в данном объеме, а убывание массовой скот рости приводит к возрастанию плотности в данном объеме. Другими словами,
приводит к убыванию плотности жидкости в данном объеме, а убывание массовой скот рости приводит к возрастанию плотности в данном объеме. Другими словами, 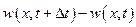 и
и 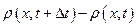 всегда будут
всегда будут
иметь противоположные знаки, т. е. знаки 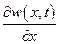 ,
, 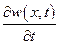 будут
будут
разные. Таким образом, если для несжимаемой жидкости  ,
,
то для сжимаемой жидкости 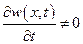 . При этом если
. При этом если 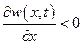 ,
,
то w (x, t) вдоль оси х убывает, т. е. больше притекает жидкости в данный объем, чем из него вытекает, что приводит к возраста-
нию плотности  во времени, или же
во времени, или же 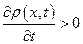 Точно
Точно
также, если 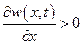 , то w (x, t) возрастает вдоль оси х, т. е.
, то w (x, t) возрастает вдоль оси х, т. е.
больше вытекает жидкости из данного объема, чем в него притекает, что приводит к убыванию плотности  во времени,
во времени,
или же  .
.
Проиллюстрируем сказанное выше на примерах.
Обозначим через 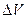 объем и положим, что
объем и положим, что 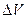 = 50 м3. Пусть количество притекающей за время
= 50 м3. Пусть количество притекающей за время 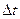 в этот объем жидкости будет G1, а количество вытекающей жидкости G2. Изменение массы в данном объеме за время
в этот объем жидкости будет G1, а количество вытекающей жидкости G2. Изменение массы в данном объеме за время 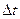 обозначим через
обозначим через  . Тогда:
. Тогда:
а) если G1= 20 кг, a G2= 19 кг, т. е. в указанный объем больше притекает жидкости, чем вытекает, то масса жидкости увеличивается на
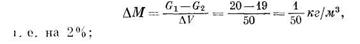
б) если Gx = 20 кг, a G2 = 21 кг, т. е. из этого объема больше вытекает жидкости, чем в него
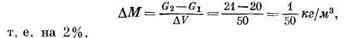
Теперь перейдем к получению математического выражения закона постоянства массы, т. е. к выводу уравнения неразрывности сжимаемой жидкости. Для одномерного движения жидкости (см. рис. 3) изменение количества жидкости 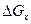 за некоторый промежуток времени
за некоторый промежуток времени 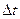 составит
составит

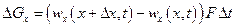 , (I.25)
, (I.25)
где F — площадь поперечного сечения трубы.
Изменение же массы в рассматриваемом объеме 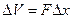 за тот же промежуток времени
за тот же промежуток времени
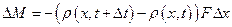 . (1.26)
. (1.26)
Как было указано выше, 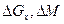 всегда будут иметь разные знаки. Приравнивая правые части (1.25) и (1.26), получаем выражение закона постоянства массы
всегда будут иметь разные знаки. Приравнивая правые части (1.25) и (1.26), получаем выражение закона постоянства массы
 .
.
В результате деления последнего выражения на 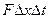 при переходе к пределу при
при переходе к пределу при 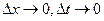 находим
находим
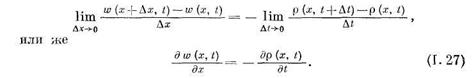
Уравнение (1.27) называется уравнением неразрывности сжимаемой жидкости при линейном течении. Правая часть, т. е. 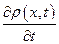 , характеризует изменение плотности жидкости
, характеризует изменение плотности жидкости  во времени, а левая часть
во времени, а левая часть 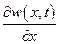 —изменение скорости вдоль оси х (оси трубы).
—изменение скорости вдоль оси х (оси трубы).
Поэтому 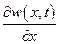 ,
, 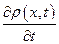 всегда будут иметь разные знаки. Уравнение (1.27) справедливо для любой точки
всегда будут иметь разные знаки. Уравнение (1.27) справедливо для любой точки 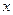 ив любой момент времени t. Это объясняется тем, что сечения х и
ив любой момент времени t. Это объясняется тем, что сечения х и 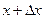 , а также моменты времени t и
, а также моменты времени t и 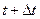 были взяты произвольно, а для получения (1.27) мы переходили к пределу при
были взяты произвольно, а для получения (1.27) мы переходили к пределу при  , т. е. формула (1.27) была получена для произвольной точки х и произвольного момента времени t. Последнее замечание относится также к случаю плоского и пространственного течения жидкости.
, т. е. формула (1.27) была получена для произвольной точки х и произвольного момента времени t. Последнее замечание относится также к случаю плоского и пространственного течения жидкости.
При плоском течении жидкости мы исходили из рис. 4. Изменение количества жидкости за промежуток времени Δt определяли по формуле
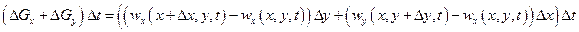 , (1.28}
, (1.28}
а изменение массы в рассматриваемом объеме — по формуле
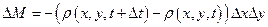 . (I.29)
. (I.29)
При выводе формул (1.28) и (1.29) рассматриваем параллелепипед с шириной, равной единице, длиной 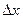 ; и высотой
; и высотой 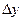 . Приравняв, правые части (1.28) и (1.29), предварительно разделив их на
. Приравняв, правые части (1.28) и (1.29), предварительно разделив их на 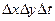 ,. и перейдя к пределу при
,. и перейдя к пределу при 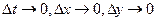 , получим
, получим

или
 (L30)
(L30)
Это уравнение называется уравнением неразрывности плоского течения сжимаемой жидкости, и справедливо оно для любой точки (х, у) в любой момент времени t.
Наконец, для получения уравнения неразрывности при течении жидкости в пространстве мы исходили из рис. 5. Изменение количества жидкости в рассматриваемом объеме 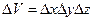 за промежуток времени Д£ определяли при помощи равенства
за промежуток времени Д£ определяли при помощи равенства
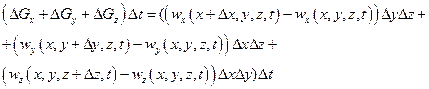 (1.31)
(1.31)
Изменение же плотности в рассматриваемом объеме 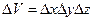 в рассматриваемый промежуток времени
в рассматриваемый промежуток времени 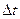 будет
будет
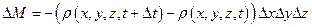 . (1.32)
. (1.32)
Приравняв правые части (1.31) и (1.32), предварительно разделив их на 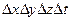 , и перейдя к пределу при
, и перейдя к пределу при 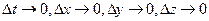 , получим
, получим
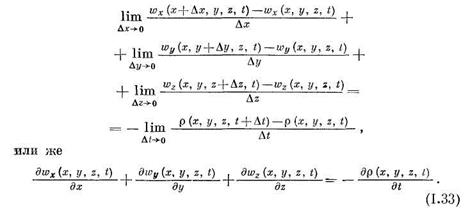
Это уравнение представляет собой уравнение неразрывности при пространственном течении сжимаемой жидкости. Правая часть уравнения  ——- характеризует изменение плотности во времени,
——- характеризует изменение плотности во времени,
а левая — изменение количества жидкости в рассматриваемом объеме.
Уравнение (1.33) справедливо для любой точки пространства
(х, у, z) в любой момент времени t. Величины 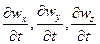 могут иметь как одинаковые, так и противоположные знаки. Однако во всех случаях знаки
могут иметь как одинаковые, так и противоположные знаки. Однако во всех случаях знаки 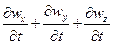 и
и  будут противоположными. Так, например, если в точках указанного объема значение
будут противоположными. Так, например, если в точках указанного объема значение 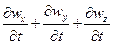 положительное (при этом
положительное (при этом 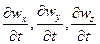 все могут быть положительными или иметь разные знаки), то это
все могут быть положительными или иметь разные знаки), то это
значит, что из указанного объема жидкости вытекает больше, чем притекает; последнее приводит к уменьшению плотности в этом
объеме во времени, т. е.  . Точно также, если значение
. Точно также, если значение
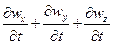 отрицательное при этом
отрицательное при этом 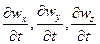 все могут быть отрицательными или же иметь разные знаки ), то в данный объем больше притекает жидкости, чем вытекает; последнее приводит к увеличению плотности во времени в этом объеме, и,
все могут быть отрицательными или же иметь разные знаки ), то в данный объем больше притекает жидкости, чем вытекает; последнее приводит к увеличению плотности во времени в этом объеме, и,
следовательно, 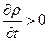 .
.
При получении уравнения неразрывности (1.33) подсчитывалось изменение массы в объеме параллелепипеда 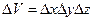 . Этот параллелепипед заполненный. Если рассмотреть фильтрацию жидкости через однородную пористую среду пористостью т, то объем г занятый жидкостью, станет равным
. Этот параллелепипед заполненный. Если рассмотреть фильтрацию жидкости через однородную пористую среду пористостью т, то объем г занятый жидкостью, станет равным 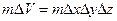 .
.
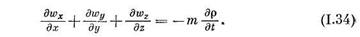 |
| Точно также для плоского и одномерного течения из уравнений (1.30) и (1.27) получим следующие уравнения неразрывности плоской и одномерной фильтрации жидкости: |
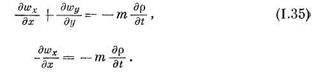 |
| Поэтому уравнение неразрывности в этом случае будет |
В случае смеси жидкостей и газов, т. е. переменности состава вдоль объема, уравнение неразрывности выводится для двухкомпонентной системы. .Состав смеси определяется массовой концентрацией с — отношением массы данного компонента к общей массе жидкости в заданном элементарном объеме.
Изменение с происходит путем механического перемешивания — состав движущегося объема не меняется, но в каждой заданной неподвижной точке, находящейся в этом месте жидкости, с со временем будет изменяться.
При диффузии под 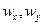 понимаются мольные скорости потока, а
понимаются мольные скорости потока, а 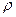 будет соответствовать концентрации. Условием диффузии является наличие градиента концентраций диффундирующего компонента (аналогично тому, как температурный градиент является условием теплопроводности). Будем считать, что накапливающая масса вызывает увеличение концентрации компонента
будет соответствовать концентрации. Условием диффузии является наличие градиента концентраций диффундирующего компонента (аналогично тому, как температурный градиент является условием теплопроводности). Будем считать, что накапливающая масса вызывает увеличение концентрации компонента 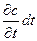 . С помощью этого прироста концентрации также можно выразить накапливающуюся и элементарном параллелепипеде массу
. С помощью этого прироста концентрации также можно выразить накапливающуюся и элементарном параллелепипеде массу 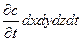 .
.
Похожие статьи:
poznayka.org
Изучаем физические свойства воды / Открытый урок
Цель урока:1. познакомить детей с новыми для них свойствами воды: текучесть, растворитель, несжимаемость, выталкивающая сила;
2. развивать мышление, речь, наблюдательность, умение анализировать, сравнивать, делать выводы; расширять кругозор учащихся;
3. воспитывать у учащихся осознанное -восприятие своего места и места человечества в окружающем мире.
Тип урока: ролевая игра в научно – исследовательскую лабораторию; изучение нового материала.
Оборудование: учебники «Окружающий мир» А. А. Вахрушев, рабочие тетради, раздаточный материал, физическая карта России, видеоряд о воде, спиртовка, пробирки, колба с водой, соль, песок, фильтр.
Ход урока
1. Организационный момент: Сегодня у нас не совсем обычный урок, а урок-исследование в научной лаборатории. Кто знает, что такое «лаборатория»? (ответы детей). Как, известно, в лаборатории должно быть всё стерильно чисто, поэтому сотрудники надевают халаты (дети надевают халатики). Теперь вы - младшие научные сотрудники, а я - руководитель нашей лаборатории. Итак, мои младшие научные сотрудники, у меня для вас задание.
2. Видеоряд. Просматривание. У детей задание - подобрать ключевое слово по видеокартинкам, (вода).
Вода самая известная и самая загадочная из всех жидкостей, существующих на Земле, (монтаж стихотворения читает учитель вместе с детьми).
Вы слыхали о воде?
Говорят, она везде!
В луже, в море, в океане
И в водопроводном кране.
Как сосулька, замерзает,
В дом туманом к нам вползает,
На плите у нас кипит,
Паром чайника шипит.
Растворяет сахар в чае.
Мы её не замечаем,
Мы привыкли, что вода-
Наша спутница всегда!
Без неё нам не умыться,
Не наесться, не напиться!
Смею я вам доложить-
Без воды нам не прожить.
3. Вопросы на повторение:
- Для чего нужна вода всем живым организмам?
- Какие природные явления связаны с переходом воды из одного состояния в другое?
4. Вступительная беседа.
Вся жизнь и деятельность человека, большинство явлений природы
связано с водой. Вода необходима для жизни всего живого на Земле.
Кстати, наше тело почти на 2/3 состоит из воды.
Вода необходима для производства строительных материалов, красок, стекла, керамики.
Вода занимает 3/4 поверхности земного шара. Толстый слой воздуха окутывает сплошной оболочкой весь земной шар. И в воздухе находится много воды в виде пара, облаков, туч. Вот, какое значение имеет вода в природе и в нашей жизни.
5. Сообщение темы урока.
6. Изучение нового материала.
Возьмём в руки пробирки с водой и опишем свойства воды, которые
Отличают её от других жидкостей: (цвет, вкус, запах).
Вместе с тем вода- жидкость, и с этим связаны её наиболее важные
свойства.
Демонстрация опыта, (сообщающиеся сосуды).
Если соединить два любых сосуда, то в них установится одинаковый
уровень жидкости. Это свойство названо законом сообщающихся сосудов.
(Учащиеся фиксируют свойство в свои рабочие папки).
Изучив это свойство воды, люди научились его использовать.
- Кто знает как? (предположения детей)
На нем основана работа фонтанов и водопроводов. ( фиксируем в рабочую
папку).
-Кто из вас знает, когда придумали водопровод? ( В Древнем Риме в 272 г.
до н.э.)
7. Физкультминутка.
8.- Следующее свойство рассмотрим на следующем опыте.
Дети по группам проделывают опыт по растворению красок, гуаши, соли.
-Что вы заметили? (ответы детей)
Вывод: Вода - хороший растворитель.
(Фиксируем это свойство в папках ).
- Как вы думаете, где применяют люди это свойство? (Ответы детей, запись-схема в папках).
- Теперь попрошу обратить внимание на колбы с раствором соли. Давайте добавим туда немного песка и попробуем размешать. (Дети проделывают опыт по группам).
- Что вы заметили? (ответы).
- Какая стала вода? (ответы).
- Вода стала солёная и грязная. Да, вода может растворять не все
вещества.
Человек зачастую виновен в загрязнении воды. Как помочь в этом случае
природе? (ответы).
- Нужно очистить воду. Дети очищают воду через фильтр.
- Что вы увидели? (ответы).
- Вода очистилась от лишних примесей, а солёный раствор остался.
9. Беседа о полезных ископаемых нашего края.
- Знаете ли вы, ребята, что в нашем крае добывают нужное всем природное ископаемое-соль.
Показ видеоматериала о добыче соли.
- Мы провели опыт похожий на работу по добыче соли: очистили, промыли, теперь надо просушить.
- Как это сделать?
Демонстрация учителем опыта о выпаривании воды.
- Что получилось в результате опыта? (Чистая соль, готовая к применению).
10. Работа с картой.
Добывают соль на озере Баскунчак (показ на карте; дети отмечают на
своих картах в папках).
- Наш край богат водными ресурсами, благодаря крупным рекам-Волге и Ахтубе, а также множеству мелких, которые образуют дельту Каспийского моря.
Дети отмечают на карте реки и море.
11. Работа с учебником.
Стр. 19. Свойство-текучесть. Запись этого свойства в папки.
-Как человек научился использовать это свойство? (ответы, запись схемы)
Стр. 20. Свойство- несжимаемость.-Как человек использует свойство несжимаемость? (ответы, запись схемы).
12. Просмотр видеостраницы о воде «Знаете ли вы?» "
13.Повторение о круговороте воды в природе.
- Знаете ли вы, ребята, о том, что если бы в природе не было бы одного
явления, то запасы воды на Земле кончились уже через 100 лет.
Что это за природное явление? (круговорот воды в природе).
- Сделайте схему круговорота в своих рабочих папках. (Проверка
выполнения).
14. Работа с раздаточным материалом в папках учащихся.
- Вода-жидкость, но только она может быть в трех состояниях. Каких? Ответ на вопрос в раздаточном материале после рассматривания рисунка: -Что заставляет крышку кастрюли подпрыгивать и греметь? (Пар).
- А может ли пар совершать работу? (Ответ на стр учебника).
15. Обобщение по теме урока.
-Прежде, чем будет подведен итог наших исследований, я бы хотела предложить вам продолжить фразу: «Вода-это...» (Дети работают в группах, зачитывают ответы от каждой группы).
16. Вывод по уроку.
- Какими свойствами обладает вода? - Как человек использует свойства воды?
17. Итог урока.
- Понравился ли вам урок?
- Интересно ли вам было почувствовать себя в роли исследователей?
18. Домашнее задание.
В природе путешествует вода.
Она не исчезает никогда:
То в снег превратится, то в лёд,
Растает и снова в поход.
По горным вершинам,
Широким равнинам
Вдруг в небо взовьётся,
Дождями вернётся,
Вокруг оглянитесь,
В природу вглядитесь...
Вас окружает везде и всегда-
Это волшебная чудо- вода.
Литература:
Пластов М. Капля в море. – М.: Детская литература, 1991.
Охрана природы / Под ред. К. В. Пашаканга. – М.: Просвещение, 1990.
Всё обо всём /Энциклопедия для детей. – М.: Слово АСТ, 1998. -Т.5
open-lesson.net
|
2. Несжимаемость.
Вода практически несжимаема. Это позволяет многим беспозвоночным
животным использовать заполненные водой полости тела в качестве
внутренней опоры организма при передвижении (т.н.
гидростатический скелет).
4. Высокая
удельная теплота парообразования.
Эта характеристика, также как и высокая температура кипения,
обусловлена наличием
водородных связей
между молекулами воды.
(Вспомните из курса физики, что
такое удельная теплота парообразования. Кстати, чтобы
выпарить, к примеру, воду из чайника, тепла потребуется в 5,5 раза
больше, чем для того, чтобы вскипятить его).Благодаря высокой теплоте
парообразования живые организмы (не только животные, но и растения)
получили возможность избавляться от избытков тепла в организме,
испаряя воду с поверхности тела или его участков. В отличие от
других способов теплообмена живых организмов с окружающей средой (излучения,
конвекции, теплопередачи)
испарение
позволяет охлаждать тело даже в том случае, когда температура
окружающей среды выше, чем температура тела.
|
|

 1.
Высокая удельная теплоемкость.
Вода имеет высокую теплоемкость (в 10 раз большую, чем
железо, и в 3300 раз большую, чем воздух). В сочетании с
высокой теплопроводностью это делает водную среду достаточно
комфортной для обитания живых организмов. (Вспомните
из курса физики, что такое удельная теплоемкость.
Среди физических характеристик среды, важных для существования в
ней живых организмов, существенную роль играют также выталкивающая
сила и вязкость, но их роль мы пока не рассматриваем.) Благодаря высокой теплоемкости и теплопроводности водная среда,
в отличие от воздушной, менее подвержена перепадам температур (как
суточным, так и сезонным), что облегчает адаптацию животных и
растений к этому абиотическому
фактору.
1.
Высокая удельная теплоемкость.
Вода имеет высокую теплоемкость (в 10 раз большую, чем
железо, и в 3300 раз большую, чем воздух). В сочетании с
высокой теплопроводностью это делает водную среду достаточно
комфортной для обитания живых организмов. (Вспомните
из курса физики, что такое удельная теплоемкость.
Среди физических характеристик среды, важных для существования в
ней живых организмов, существенную роль играют также выталкивающая
сила и вязкость, но их роль мы пока не рассматриваем.) Благодаря высокой теплоемкости и теплопроводности водная среда,
в отличие от воздушной, менее подвержена перепадам температур (как
суточным, так и сезонным), что облегчает адаптацию животных и
растений к этому абиотическому
фактору. Вопрос 1.
Каково значение этой
физической характеристики для внутриклеточных процессов? (Для ответа
на вопрос вспомните из курса химии понятия экзотермических и
эндотермических реакций).
Вопрос 1.
Каково значение этой
физической характеристики для внутриклеточных процессов? (Для ответа
на вопрос вспомните из курса химии понятия экзотермических и
эндотермических реакций). 3.
Высокая температура кипения.
Близкие по молекулярной массе вещества - метан и аммиак - при
н.у. являются газами. Вода же - жидкость и остается ею при
нагревании до 100оС. Аномально высокая температура
кипения - результат того, что молекулы воды связаны между
собою водородными связями.
(Вспомните?) Именно на разрыв этих связей
и тратится большое количество энергии.
Для обитателей водной среды это также важно. Диапазон температур
на планете (средняя + 7оС) практически не достигает
верхней границы, точки кипения воды.
3.
Высокая температура кипения.
Близкие по молекулярной массе вещества - метан и аммиак - при
н.у. являются газами. Вода же - жидкость и остается ею при
нагревании до 100оС. Аномально высокая температура
кипения - результат того, что молекулы воды связаны между
собою водородными связями.
(Вспомните?) Именно на разрыв этих связей
и тратится большое количество энергии.
Для обитателей водной среды это также важно. Диапазон температур
на планете (средняя + 7оС) практически не достигает
верхней границы, точки кипения воды. Статья Джирла Уолкера
Статья Джирла Уолкера
 Рисунок - гиперссылка на видеофрагмент
vodomer.avi (314 кб)
Рисунок - гиперссылка на видеофрагмент
vodomer.avi (314 кб)

















