Значение слова когерентность. Когерентность воды

Когерентные волны: определение, пакеты, время

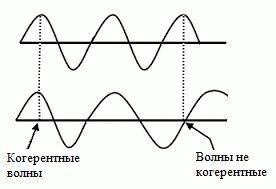
Когерентные волны – это колебания с постоянной разностью фаз. Разумеется, условие выполняется не в каждой точке пространства, лишь на отдельных участках. Очевидно, что для удовлетворения определению частоты колебаний также предвидятся равными. Прочие волны бывают когерентны лишь на некотором участке пространства, а дальше разность фаз меняется, и это определение использовать уже нельзя.

Обоснование применения

Когерентные волны считаются упрощением, не встречающимся на практике. Математическая абстракция помогает во многих отраслях науки: космос, термоядерные и астрофизические исследования, акустика, музыка, электроника и, конечно, оптика.

Для реальных приложений применяются упрощённые методы, в числе последних трёхволновая система, основы применимости которой вкратце изложены ниже. Для анализа взаимодействия возможно задать, к примеру, гидродинамическую или кинетическую модель.

Интерференция волн

Решение уравнений для когерентных волн позволяет предсказать устойчивость систем, функционирующих с использованием плазмы. Теоретический подсчёт показывает, что иногда амплитуда результата за короткий период растёт до бесконечности. Что означает создание взрывоопасной ситуации. Решая уравнения для когерентных волн, подбором условий удаётся избежать неприятных последствий.

Определения

Вначале введём ряд определений:

Монохроматической называется волна единственной частоты. Ширина её спектра равна нулю. На графике это единственная гармоника.
Спектр сигнала – графическое представление амплитуды слагающих гармоник, где по оси абсцисс (ось Х, горизонтальная) откладывается частота. Спектром синусоидального колебания (монохроматической волны) становится единственная спектринка (вертикальная чёрточка).
Преобразованиями Фурье (обратным и прямым) называют разложение сложного колебания на монохроматические гармоники и обратное сложение целого из разрозненных спектринок.
Волновой анализ цепей для сложных сигналов не проводится. Вместо этого происходит разложение на отдельные синусоидальные (монохроматические) гармоники, для каждой сравнительно просто составить формулы описания поведения. При расчёте на ЭВМ этого хватает для анализа любых ситуаций.

Спектр любого непериодического сигнала бесконечен. Границы его обрезаются до разумных пределов перед проведением анализа.
Дифракцией называется отклонение луча (волны) от прямолинейной траектории вследствие взаимодействия со средой распространения. К примеру, проявляется при преодолении фронтом щели в препятствии.
Интерференцией называется явление сложения волн. Из-за чего наблюдается весьма причудливая картина из чередующихся полос света и тени.
Рефракцией называется преломление хода волны на разделе двух сред с различными параметрами.

Волны колебаний

Понятие когерентности

Советская энциклопедия говорит, что волны одной частоты всегда когерентны. Это верно исключительно для отдельно взятых неподвижных точек пространства. Фаза определяет результат сложения колебаний. К примеру, противофазные волны одной амплитуды дают прямую линию. Такие колебания гасят друг друга. Самая большая амплитуда у синфазных волн (разность фаз равна нулю). На этом факте основан принцип действия лазеров, зеркальная и фокусирующая системы которых, особенности получения излучения делают возможной передачу информации на колоссальные расстояния.

Согласно теории взаимодействия колебаний когерентные волны образуют интерференционную картину. У новичка возникает вопрос: свет лампочки не кажется полосатым. По простой причине, что излучение не одной частоты, а лежит в пределах отрезка спектра. И участок, причём, приличной ширины. Из-за неоднородности частот волны беспорядочные, не проявляют свои теоретически и экспериментально в лабораториях обоснованные и доказанные свойства.

Хорошей когерентностью обладает луч лазера. Его используют для связи на дальние расстояния при прямой видимости и прочих целей. Когерентные волны дальше распространяются в пространстве и на приёмнике подкрепляют друг друга. В пучке света разрозненной частоты эффекты способны вычитаться. Возможно подобрать условия, что излучение исходит от источника, но на приёмнике не зарегистрируется.

Обычный свет лампочки тоже работает не на полную мощность. Достичь КПД в 100% на современном этапе развития техники не представляется возможным. К примеру, газоразрядные лампы страдают сильной дисперсией частот. Что касается светодиодов, основатели концепции нанотехнологий обещали создать элементную базу для производства полупроводниковых лазеров, но воз и ныне там. Значительная часть разработок вовсе засекречена и рядовому обывателю недоступна.

Итак, лишь когерентные волны проявляют волновые качества. Действуют согласованно, как лучинки веника: по одной легко сломать, но вместе взятые — выметают мусор. Волновые свойства – дифракция, интерференция и рефракция – характерны для всех колебаний. Просто зарегистрировать эффект сложнее из-за беспорядочности процесса.

Когерентные волны не демонстрируют дисперсии. Показывают одну частоту и одинаково отклоняются призмой. Все примеры волновых процессов в физике даются, как правило, для когерентных колебаний. На практике приходится учитывать присутствующую малую ширину спектра. Что накладывает особенности на процесс расчёта. Как зависит реальный результат от относительной когерентности волны — пытаются ответить многочисленные учебники и разрозненные издания с замысловатыми названиями! Единого ответа не существует, он сильно зависит от отдельно взятой ситуации.

Волновые пакеты

Для облегчения решения практической задачи можно ввести, к примеру, определение волнового пакета. Каждый из них разбивается дальше на мелкие части. И эти подразделы взаимодействуют когерентно между аналогичными частотами другого пакета. Подобный аналитический метод широко распространён в радиотехнике и электронике. В частности, понятие спектра изначально вводилось для того, чтобы дать в руки инженеров надёжный инструмент, позволяющий оценить поведение сложного сигнала в конкретных случаях. Оценивается малая толика воздействия каждого гармонического колебания на систему, потом конечный эффект находится их полным сложением.

Следовательно, при оценке реальных процессов, не являющихся даже близко когерентными, допустимо разбить объект анализа на простейшие составляющие, чтобы оценить результат процесса. Расчёт упрощается с применением вычислительной техники. Машинные эксперименты показывают достоверность формул для имеющейся ситуации.

На начальном этапе анализа полагают, что пакеты с малой шириной спектра возможно условно заменить гармоническими колебаниями и в дальнейшем пользоваться обратным и прямым преобразованием Фурье для оценки результата. Эксперименты показали, что разброс фаз между выбранными пакетами постепенно возрастает (колеблется с постепенным увеличением разброса). Но для трёх волн разница постепенно сглаживается, согласуясь с излагаемой теорией. Накладывается ряд ограничений:

Пространство должно быть бесконечным и однородным (k-пространство).
Амплитуда волны не затухает с увеличением дальности, но меняется с течением времени.

Доказано, что в такой среде каждой волне удаётся подобрать конечный спектр, что автоматически делает возможным машинный анализ, а при взаимодействии пакетов спектр результирующей волны уширяется. Колебания по сути когерентными не считаются, но описываются уравнением суперпозиции, представленном ниже. Где волновой вектор ω(k) определяется по дисперсионному уравнению; Еk признано амплитудой гармоники рассматриваемого пакета; k – волновое число; r – пространственная координата, для которой решается представленное уравнение; t – время.

Уравнение суперпозиции

Время когерентности

В реальной ситуации разнородные пакеты когерентны лишь на отдельном интервале. А далее расхождение фаз становится слишком большим, чтобы применять описанное выше уравнение. Чтобы вывести условия возможности вычислений, вводится понятие времени когерентности.

Полагается, что в начальный момент фазы всех пакетов одинаковы. Выбранные элементарные доли волны когерентны. Тогда искомое время находится как отношение числа Пи к ширине спектра пакета. Если время превысило когерентное, в данном участке уже нельзя использовать формулу суперпозиции для сложения колебаний — фазы слишком сильно отличаются друг от друга. Волна уже не когерентна.

Пакет возможно рассматривать так, будто он характеризуется случайной фазой. В этом случае взаимодействие волн идёт по иной схеме. Тогда находятся фурье-компоненты по указанной формуле для дальнейших расчётов. Причём взятые для расчёта две другие компоненты могут быть из трёх пакетов. Это случай совпадения с теорией, о котором говорилось выше. Следовательно, уравнение показывает зависимость всех пакетов друг от друга. Точнее – результата сложения.

Для получения наилучшего результата нужно, чтобы ширина спектра пакета не превышала числа Пи, делённого на время, в течение которого решается задача суперпозиции когерентных волн. При расстройке частоты амплитуды гармоник начинают осциллировать, точный результат получить сложно. И наоборот, для двух когерентных колебаний формула сложения упрощается максимально. Амплитуда находится как квадратный корень из суммы исходных гармоник, возведённых в квадрат и сложенных с собственным удвоенным произведением, помноженным на косинус разности фаз. У когерентных величин угол равен нулю, результат, как уже указано выше, получается максимальным.

Наравне с временем и длиной когерентности используют термин «длина цуга», что является аналогом второго термина. Для солнечного света эта дистанция составляет один микрон. Спектр нашего светила крайне широкий, что объясняет столь мизерную дистанцию, на которой его излучение считается когерентным самому себе. Для сравнения, длина цуга газового разряда достигает 10 см (в 100000 раз больше), а у лазера излучение сохраняет свойства и на километровых расстояниях.

С радиоволнами намного проще. Кварцевые резонаторы позволяют достичь высокой когерентности волны, чем объясняются пятна уверенного приёма на местности, граничащие с зонами молчания. Аналогичное проявляется при изменении имеющейся картины с течением суток, движением облаков и прочими факторами. Изменяются условия распространения когерентной волны, и интерференционная суперпозиция оказывает влияние в полной мере. В радиодиапазоне на низких частотах длина когерентности может превышать поперечник Солнечной системы.

Условия сложения сильно зависят от формы фронта. Наиболее просто задача решается для плоской волны. Но на деле фронт обычно является сферическим. Точки синфазности находятся на поверхности шара. В бесконечно удалённой от источника местности условие плоскости можно принять за аксиому, и дальнейший расчёт вести согласно этому постулату. Чем ниже частота, тем проще создать условия для выполнения расчёта. И наоборот, источники света со сферическим фронтом (вспомним Солнце) очень сложно подогнать под стройную теорию, написанную в учебниках.

vashtehnik.ru

Когерентные волны материи

Дмитрий Паращук,доктор физико-математических наук«Химия и жизнь» №3, 2007

Нас окружают предметы определенных размеров; мы точно знаем, где кончается наше тело, и уверены, что на одном стуле комфортно сидеть только одному. Однако в мире очень маленьких вещей, или в микроквантовом мире, всё не так прозаично: стул и стол, уменьшенные примерно в десять миллиардов раз, до размеров атомов, потеряют свои четкие границы и даже могут занять одно место в пространстве, ничуть не мешая друг другу. Причина в том, что объекты квантового мира больше похожи на волны, проникающие друг в друга, чем на ограниченные в пространстве предметы. Поэтому в микроквантовом мире можно сидеть на одном стуле и втроем, и вдесятером.

Вещи как волны

Чтобы волновые свойства можно было почувствовать экспериментально, объекты нужно сделать не только маленькими, но и очень холодными, то есть с сильно пониженной скоростью хаотического движения атомов. Так, атомы требуется охладить до миллиардной доли градуса Кельвина, а волновые свойства стола и стула из макромира должны быть заметны при немыслимо маленьких температурах — холоднее, чем 10–40 К.

Примечательное свойство волн — их способность когерентно складываться. Когерентно — значит согласованно, упорядоченно во времени или в пространстве. Пример когерентных во времени звуковых волн — музыка. Каждый звук мелодии, его высота, продолжительность и сила находятся в строго определенном соответствии друг с другом.

Дирижер симфонического оркестра пристально следит за когерентностью звукового потока из сотен, а то и тысяч звуков. Ослабление когерентности мы воспримем как фальшивое звучание, а ее полную потерю — как шум. Собственно, когерентность и отличает мелодию от бессвязного набора звуков. Точно так же и в квантовом мире когерентность волновых свойств объектов способна придать им совершенно новые качества, которые не только очень необычны, но и важны для создания новых материалов, способных радикально изменить существующие технологии. Не случайно почти половина Нобелевских премий по физике, присужденных за последние десять лет, связана с когерентными явлениями: в лазерном излучении (2005), в холодных атомах (1997, 2001), в жидком гелии (1996) и в сверхпроводниках (2003).

Большинство отечественных нобелевских лауреатов по физике получило свои премии за когерентные явления: Петр Капица (1978), Лев Ландау (1962), Николай Басов и Александр Прохоров (1964), Алексей Абрикосов и Виталий Гинзбург (2003).

Когерентность света

Понятие когерентности сформировалось в начале XIX века после опытов английского ученого Томаса Юнга. В них две световые волны от разных источников падали на экран и складывались. Свет от двух обычных лампочек, которые дают некогерентное излучение, складывается просто: освещенность экрана равна сумме освещенностей от каждой лампы. Механизм тут такой. У световых волн от лампочек разность фаз хаотически меняется с течением времени. Если в одну точку экрана сейчас пришли два максимума волны, то в следующий момент от одной лампы может прийти минимум, а от другой — максимум. Результат сложения волн даст «рябь на воде» — неустойчивую интерференционную картину. Рябь световых волн столь быстра, что глаза не успевают за ней и видят равномерно освещенный экран. По аналогии из мира звуков — это шум.

Рис. 1. При освещении экрана двумя пучками лазера возникает интерференционная картина из чередующихся ярких и тусклых полос (интерферограмма Лаборатории адаптивной оптики Шатурского отд. Московского государственного открытого университета) Изображение: «Химия и жизнь»

Результат будет совсем другим, если на экране складываются две когерентные волны (рис. 1). Такие волны проще всего получить из одного лазерного пучка, расщепив его на две части, а потом их сложив. Тогда на экране возникнут полосы. Яркие — это области экрана, куда максимумы световых волн всегда приходят одновременно (в фазе). Замечательный оптический эффект состоит в том, что освещенность возрастет не в два раза, как в случае некогерентных волн, а в четыре. Это происходит потому, что в яркой полосе все время складываются максимумы волн, то есть их амплитуды, а освещенность пропорциональна квадрату суммы амплитуд волн. В тусклых полосах когерентные волны от разных источников гасят друг друга.

Теперь представим себе много когерентных волн, приходящих в некоторую точку в фазе. Например, тысячу волн. Тогда освещенность яркой области вырастет в миллион раз! Когерентное излучение огромного, около 1022, числа атомов дает луч лазера. Изобретение принципов его работы принесло в 1964 году Нобелевскую премию по физике американцу Чарльзу Таунсу и двум советским физикам Николаю Басову и Александру Прохорову. За 40 лет лазер проник в нашу повседневную жизнь, с его помощью мы, например, сохраняем информацию на компактных дисках и передаем ее по оптическому волокну на огромные расстояния.

Когерентные волны материи

Наш мир устроен таким образом, что каждая частица вещества может проявлять свойства волны. Такие волны называют волнами материи, или волнами де Бройля. Замечательный французский физик Луи де Бройль в 1923 году предложил очень простую формулу, связывающую длину волны λ (расстояние между максимумами) с массой частицы m и ее скоростью v: λ = h/mv, где h — постоянная Планка.

Фундаментальное свойство волн любой природы — способность интерферировать. Однако чтобы в результате получить не равномерный шум, а, как и в случае со светом, яркую полосу, нужно обеспечить когерентность волн де Бройля. Этому мешает тепловое движение — атомы с разными скоростями различаются своими длинами волн. При охлаждении атомов, согласно формуле де Бройля, растет длина волны λ (рис. 2). И как только ее значение превысит расстояние между частицами, волны де Бройля разных частиц дадут устойчивую интерференционную картину, так как максимумы волн, отвечающие положению частиц, будут перекрываться.

Рис. 2. Каждую частицу (атом, молекулу) можно представить в виде волны де Бройля у волнового пакета, центр которого соответствует центру частицы. По мере охлаждения, то есть снижения скорости хаотического движения частицы, длина волны растет, и волновые пакеты частиц в конце концов перекрываются. (Изображение: «Химия и жизнь»)

В оптический микроскоп интерференционную картину волн де Бройля можно увидеть, если их длины будут около 1 мкм. Для этого, как следует из формулы де Бройля, скорость атома должна быть примерно 1 см/с, что соответствует чрезвычайно низким температурам — менее одного микрокельвина. Такой охлажденный газ из атомов щелочных металлов удалось приготовить, и сегодня это интереснейший объект исследований. (Как охладить атомы до низких температур и сделать на их основе сверхточные часы, было рассказано в «Химии и жизни», 2001, № 10. — Примеч. ред.) Отметим, что советские физики из Института спектроскопии АН СССР во главе с Владиленом Летоховым в 1979 году выдвинули и реализовали ключевые идеи, на основе которых сейчас охлаждают атомы до сверхнизких температур.

Что представляют собой интерферирующие частицы вещества? Мы привыкли, что вещество можно представить в виде твердых маленьких шариков, которые не проникают друг в друга. А волны, напротив, могут складываться и проникать друг в друга. По аналогии с интерференцией света мы должны получить «яркую точку на экране» — малую область в пространстве, где максимумы волн материи складываются в фазе. Неожиданно то, что когерентные волны многих и многих атомов могут занять одну область в пространстве, образуя как бы сверхатом — набор огромного числа волн де Бройля. На языке квантовой механики это означает, что вероятность обнаружить когерентные атомы в «яркой точке» максимальна. Это удивительное состояние вещества называют конденсатом Бозе—Эйнштейна. Альберт Эйнштейн предсказал его в 1925 году на основании работ индийского физика Шатьендраната Бозе. В конденсате все атомы находятся в одном квантовом состоянии и ведут себя как одна большая волна.

Рис. 3. Иллюстрация интерференции двух атомных конденсатов: а — два конденсата в отдельных ловушках; б — после отключения ловушек конденсаты расширяются,перекрываясь друг с другом. В области их перекрытия возникает интерференционная картина. (Изображение: «Химия и жизнь»)

Экспериментально наблюдать бозе-эйнштейновский конденсат (БЭК) удалось только спустя 70 лет: сообщение об этом в 1995 году опубликовали две группы американских ученых. В их экспериментах в конденсат выпадали атомы из облачка паров натрия или рубидия, запертого в магнитную ловушку. Эти пионерские работы были удостоены Нобелевской премии по физике 2001 года, присужденной Эрику Корнеллу, Вольфгангу Кеттерле и Карлу Вьеману. Яркое образное представление поведения сверххолодных атомов, выпадающих в БЭК, было показано на обложке декабрьского журнала Science за 1995 год: в центре марширует группа одинаковых синих киборгов — это атомы БЭК с нулевой температурой, а вокруг них хаотично двигаются киборги более теплых цветов — надкондесатные чуть-чуть разогретые атомы. Когерентность атомов, выпавших в БЭК, была продемонстрирована в блестящем эксперименте 1997 года В. Кеттерле с коллегами из Массачусетсского технологического института. Для этого магнитную ловушку разделили на две части перегородкой из света (рис. 3а). Из облачков атомов натрия приготовили два конденсата, а затем ловушку и перегородку отключили: облачка стали расширяться и перекрываться. В месте их перекрытия возникала четкая интерференционная картина (рис. 3б), подобная интерференции когерентных лазерных пучков (см. рис. 1). Ее наблюдали по тени, отбрасываемой облачком атомов на экран, — «зебра» на рис. 3б и есть тень интерферирующих волн материи; темные области соответствуют максимумам волн атомов. Удивительно, что когда мы складываем атомы из разных конденсатов, то их сумма может дать ноль — «вещество исчезает» в области, отвечающей светлой полосе «зебры». Разумеется, на самом деле атомы не исчезают — они просто концентрируются в областях, отбрасывающих тень.

Можно ли наблюдать проявление волновых свойств для более массивных объектов, чем атомы? Оказывается, можно. Группе Антона Цайлингера из Вены в 2003 году удалось наблюдать интерференцию фуллеренов и биомолекул, содержащих около ста атомов. Для сколь больших частиц вещества удастся наблюдать волновые свойства — вопрос на сегодня открытый.

Атомный лазер

С точки зрения квантовой физики атомы и фотоны похожи тем, что большое число этих частиц может одновременно находиться в одном квантовом состоянии, то есть быть когерентными. Например, в лазерном излучении все фотоны когерентны: у них одинаковый цвет, направление распространения и поляризация. Поэтому возможно получить мощные когерентные лазерные пучки, состоящие из огромного числа фотонов в одном состоянии.

А как получить когерентные атомные пучки? Идея проста: надо аккуратно вывести запертые в ловушку когерентные атомы из БЭК, подобно тому, как излучение лазера выводится из его резонатора с помощью полупрозрачного зеркала. Такое устройство назвали атомным лазером. Первый атомный лазер в 1997 году создал все тот же В. Кеттерле. В таком лазере магнитная ловушка из двух катушек удерживает атомы натрия, образующие БЭК. Импульсы радиополя, прикладываемые с периодом 5 миллисекунд, разворачивают спины атомов, и они не могут больше удерживаться в ловушке. Сгусток освободившихся атомов — излучение атомного лазера — свободно падает под действием гравитации, что визуализируют с помощью приемов театра теней, описанных выше. Сегодня мощность атомных лазеров невелика: они излучают 106 атомов в секунду, что несравненно меньше мощности оптических лазеров. Так, например, обычный лазер-указка излучает за одну секунду примерно в 109 раз больше фотонов.

В отличие от невесомых фотонов, атомы обладают массой покоя. А значит, тяготение гораздо сильнее действует на них — интерференция когерентных волн материи будет сильно зависеть от гравитационного поля, отклоняющего пучки атомов. Пусть два когерентных атомных пучка интерферируют в области их пересечения аналогично лазерным пучкам (см. рис. 1). Предположим, что гравитационное поле на пути одного из атомных пучков изменилось. Тогда длина пути этого пучка до встречи с другим пучком также изменится. В результате максимумы волн материи двух атомных пучков встретятся в другом месте, что приведет к смещению интерференционной картины. Измеряя такое смещение, можно определить изменение гравитационного поля. На основе этой идеи уже созданы датчики гравитационного поля, способные обнаружить разницу в величине ускорения свободного падения менее 10–6%. Они могут пригодиться как для фундаментальных исследований (проверка физических теорий, измерение констант), так и для важных прикладных разработок в навигации (создание прецизионных гироскопов), геологии (зондированием полезных ископаемых) и для других наук. У писателей-фантастов, например, можно найти сюжет, когда с помощью прибора для измерения малейших изменений силы тяжести археологи читают надписи, выбитые на погребенных в толще земли обелисках.

Когерентное вещество

Особенно интересные эффекты возникают, когда свойства когерентных волн материи удается наблюдать как макроскопические свойства конденсированного вещества, то есть твердого тела или жидкости. Один из ярких примеров таких свойств — сверхтекучесть в жидком гелии при охлаждении ниже 2,2 К. Советские физики выполнили пионерские исследования сверхтекучести: это явление открыл Петр Капица в 1938 году, а объяснил Лев Ландау. Сверхтекучий гелий может вытекать через маленькие отверстия с огромной скоростью: по крайней мере, в 108 раз быстрее воды. Если бы нам удалось наполнить обычную ванну сверхтекучим гелием, то он вытек бы из нее менее чем за одну секунду через дырочку размером с крохотное игольное ушко. В 2004 году американцы Юн Сён Ким и Мозес Чан сообщили об обнаружении сверхтекучести в твердом гелии. Их тонкий эксперимент состоял в следующем: твердый охлажденный гелий, находящийся под давлением при температуре около 0,2 К, помещали на крутильный маятник. Если часть гелия переходит в сверхтекучее состояние, то частота крутильных колебаний должна вырастать, так как сверхтекучая компонента остается неподвижной, облегчая колебания маятника. По данным Кима и Чана, в сверхтекучее состояние переходило около 1% твердого гелия. Эти эксперименты демонстрируют, что атомы могут свободно перемещаться по сверхтекучему твердому телу, следовательно, оно способно пропускать массу вещества сквозь себя беспрепятственно: перспектива проходить сквозь стены в таком мире кажется вполне реальной!

Это удивительное явление могут объяснить волновые свойства атомов. Волны, в отличие от частиц, обходят препятствия на своем пути. Поясним это на примере интерференции двух пучков света на экране. Вырежем в экране отверстия в области светлых полос «зебры» (интерференционной картины). Такое препятствие когерентный свет не почувствует: экран ведь сохранился только в неосвещенных частях «зебры». Если же пучки не когерентны, то равномерно освещенный экран с отверстиями неизбежно задержит часть света. Отсюда можно уяснить, как когерентные волны материи преодолевают препятствия без потерь.

Еще одно необычное макроскопическое квантовое явление, аналогичное сверхтекучести, — сверхпроводимость, открытая голландцем Хейке Камерлингом-Онессом в 1911 году в ртути при ее охлаждении до температуры жидкого гелия (Нобелевская премия 1913 года). Сверхпроводящие электроны двигаются без сопротивления, обходя препятствия, в роли которых выступает тепловое движение атомов. Например, ток в кольце из сверхпроводника может течь неограниченно долго, поскольку ему ничто не мешает. Можно сказать, что сверхпроводимость есть сверхтекучесть электронной жидкости. Для такой сверхтекучести нужно, чтобы большое число зарядов находилось в одном квантовом состоянии, как, например, фотоны в лазерном пучке. Это требование наталкивается на ограничение, установленное выдающимся швейцарским физиком Вольфгангом Паули в 1924 году: если спиновое число частицы равно 1/2, как у электрона, то в одном квантовом состоянии может находиться лишь одна частица. Такие частицы называют фермионами. При целом значении спина в одном квантовом состоянии можно сконденсировать сколь угодно большое число частиц. Такие частицы называют бозонами. Поэтому для сверхпроводящего тока нужны частицы электрического заряда с целым спином. Если бы пара электронов (фермионов) смогла сформировать составную частицу, то спин пары оказался бы целым числом. И тогда составные частицы станут бозонами, способными образовать БЭК и дать сверхпроводящий ток.

Однако связанные пары электронов действительно могут возникать в проводниках, несмотря на то что кулоновские силы отталкивают электроны друг от друга — эта идея легла в основу теории, объясняющей сверхпроводимость в простых металлах (Джон Бардин, Леон Купер, Джон Шриффер, Нобелевская премия по физике за 1972 год).

Сверхтекучесть БЭК

Рис. 4. Наблюдение сверхтекучести в бозе-эйнштейновском атомном конденсате; а — конденсат (красный) захвачен лазерным пучком (розовый) и магнитными катушками (синие кольца). Два дополнительных лазерных пучка (зеленые), проходящие по краям конденсата, вращаются вокруг оси системы, увлекая конденсат за собой; б — после выключения ловушки конденсат расширяется, отбрасывая тень при освещении (красная стрелка). Изображение: «Химия и жизнь»

Итак, во второй половине XX века физики пришли к пониманию, что БЭК может обладать свойствами сверхтекучести. Естественно, что после получения газового БЭК ученых захватила идея об экспериментах, демонстрирующих в нем сверхтекучесть. В 2005 году группа В. Кеттерле представила окончательное доказательство сверхтекучести газового БЭК. Идея эксперимента основана на том, что сверхтекучая жидкость ведет себя при вращении необычно. Если бы нам удалось размешать сверхтекучую жидкость ложкой, будто кофе в чашке, то она стала бы вращаться не целиком, а распалась бы на множество маленьких вихрей. Более того, они расположились бы в строгом порядке, образуя так называемую решетку вихрей Абрикосова. Схема этого филигранного эксперимента следующая (рис. 4). Газовый конденсат, захваченный лазерным пучком и магнитным полем, начинали вращать дополнительными лазерными пучками; они раскручивали конденсат, как ложечка — кофе. Затем ловушку, то есть пучки и катушку, отключали, и конденсат был предоставлен сам себе. Он расширялся и давал тень, которая напоминала швейцарский сыр (рис. 4б). «Дырочки в сыре» отвечают сверхтекучим вихрям. Важнейшая особенность этих экспериментов состоит в том, что они проделаны не только в газе бозонов (атомов натрия), но и в газе фермионов (атомов лития). Сверхтекучесть в литиевом газе наблюдали только тогда, когда атомы лития образовывали молекулы или слабые пары. Это было первое наблюдение сверхтекучести газа фермионов. Оно подвело прочный экспериментальный фундамент под теорию сверхпроводимости, основанную на идее конденсации Бозе—Эйнштейна.

Спаривать атомы лития физикам удается с помощью так называемого резонанса Фешбаха, который возникает в ловушке при одновременном действии полей магнитных катушек и лазерных пучков. Магнитное поле подстраивают в области резонанса Фешбаха так, что оно сильно изменяет силы взаимодействия между атомами газа. Можно заставить атомы притягиваться друг к другу или — отталкиваться. Физики придумали и другие способы управления свойствами сверххолодного атомного газа. Один из самых изящных — поместить атомы в интерферирующее поле лазерных пучков — своеобразную оптическую решетку. В ней каждый атом окажется в центре одной из полос интерференционной картины (см. рис. 1), так что волны света будут удерживать волны вещества, подобно форме для хранения яиц. Атомы в оптической решетке служат отличной моделью кристалла, где с помощью параметров лазерных пучков меняют расстояние между атомами, а с помощью резонанса Фешбаха — регулируют взаимодействие между ними. В результате физики реализовали давнюю мечту — получать образец вещества с управляемыми параметрами. Ученые полагают, что сверххолодный газ — модель не только кристалла, но и более экзотических форм материи, таких, как нейтронные звезды и кварк-глюонная плазма ранней Вселенной. Поэтому некоторые исследователи не без основания полагают, что сверххолодный газ поможет понять ранние этапы эволюции Вселенной.

Когерентное будущее

Явления сверхтекучести и сверхпроводимости показывают, что когерентность волн де Бройля большого числа частиц дает неожиданные и важные свойства. Эти явления не были предсказаны, более того, на объяснение сверхпроводимости в простых металлах потребовалось почти 50 лет. А явление высокотемпературной сверхпроводимости, обнаруженное в 1986 году в металло-оксидных керамиках при 35 градусах Кельвина немцем Йоханесом Беднорцем и швейцарцем Карлом Мюллером (Нобелевская премия 1987 года), до сих пор не получило общепринятого объяснения, несмотря на огромные усилия физиков во всем мире.

Еще одна область исследований, в которой без когерентных квантовых состояний не обойтись, — квантовые компьютеры: только в таком состоянии есть возможность проводить высокопроизводительные квантовые вычисления, недоступные самым современным суперкомпьютерам.

Итак, когерентность означает сохранение разности фаз между складывающимися волнами. Сами волны могут быть различной природы: и световыми, и волнами де Бройля. На примере газового БЭК мы видим, что когерентное вещество фактически представляет собой новую форму материи, ранее недоступную человеку. Возникает вопрос: всегда ли наблюдение когерентных квантовых процессов в веществе требует очень низких температур? Не всегда. По крайней мере, есть один очень удачный пример — лазер. Окружающая температура для работы лазера обычно не существенна, так как лазер работает в условиях, далеких от теплового равновесия. Лазер — сильно неравновесная система, поскольку к нему подводится поток энергии.

По-видимому, мы находимся еще в самом начале исследований когерентных квантовых процессов с участием огромного числа частиц. Один из волнующих вопросов, на который пока нет определенного ответа, — встречаются ли макроскопические когерентные квантовые процессы в живой природе? Может быть, саму жизнь можно характеризовать как особое состояние вещества с повышенной когерентностью.

elementy.ru

Творческое объединение авторов и разработчиков «БИОСТИМ»

ТОАиР "БИОСТИМ"

О воде в наше время не писал разве только ленивый… На сайте «Все о воде» (/) опубликовано более 1000 работ. Среди этих работ есть замечательная обзорная статья к.х.н. О.В. Мосина «Современная модель воды» (/article2268), в которой рассматриваются практически все гипотезы образования квазикристаллических структур в воде. Эти гипотезы объясняют образование из молекул воды различных структур, но не дают физического объяснения одного широко известного факта – повышенной электропроводности структурированной воды.

Ответ на это вопрос можно найти в гипотезе когерентных доменов (КД) профессора Миланского университета Эмилио дель Джудиче (Emilio Del Giudice), которая стала широко известна в 2007 года русскоязычному читателю после публикации перевода его лекции на 7-й Летней школе «Биофотоника и приложения биофотонов» (medscience.asia/articles/kogerentnaya-kvantovo-elektrodinamicheskaya-organizatsiya-biokhimicheskikh-protsessov

Согласно этой гипотезы в возбужденном состоянии многие электроны в молекулах воды почти свободны, и требуется совсем немного энергии, чтобы они стали полностью свободными. С позиций электрохимии можно сказать, что в некогерентном состоянии молекулы воды не могут выступать в качестве восстановителей — доноров электронов, а когерентная вода — хороший восстановитель. Более того, некогерентная вода удерживает электроны столь прочно, что может рассматриваться даже как мягкий окислитель, потому что ее молекула может удержать еще один электрон, превратившись в ион Н2О‾, тогда как в когерентном состоянии вода легко отдает электроны, превращаясь в ионы Н2О+. Поэтому если бы удалось разделить когерентную и некогерентную воду, то возникла бы электрическая батарея и возможность получения электродвижущей силы. Но обычная вода к этому неспособна, потому что обе фазы — некогерентная и когерентная — смешаны друг с другом, правда, на микроскопическом уровне эксперимент мог бы получиться.

Итак, когерентный домен окружен облаком квази-свободных электронов. Эту электронную плазму мы можем возбудить очень малой порцией энергии, меньше 0,2 эВ. Возбуждение превращает электронную плазму в микровихрь, вращающийся вокруг КД. Таким образом, любой внешний шум может превращать когерентные домены воды в вихри, когерентные вихри. Например, при простом перемешивании или встряхивании воды небольшие порции освобождающейся энергии способны продуцировать вращение вихрей, принадлежащих когерентным доменам, когда квази-свободные электроны начинают вращаться с частотой порядка килогерц. Это вращение — движение без трения, поскольку когерентность подразумевает, что вся эта масса молекул движется не как толпа, а как балет, не испытывая столкновений. Движение без трения может длиться очень долго. Оно может не затухать в течение многих часов, недель, и даже лет.

Для проверки этой гипотезы мы использовали БЭСТ-4м8, который позволяет создать когерентные домены в воде и превратить воду в источник электродвижущей силы. Приводим протокол эксперимента.

Объект исследования – дистиллированная вода ГОСТ 6709-72 , помещенная в мерный стакан из пищевой пластмассы, объем воды -150 мл.

Для измерений использовались электроды В.Г. Макаца (донор электронов – пластина из сплава АМЦ, площадь покрытия водой 20 см2). Кратчайшее расстояние между электродами 40 мм.

Прибор измерения – цифровой мультиметр DT-830B в режиме измерения напряжения со шкалой 0 – 2000 mV.

Температура в помещении 22оС, атмосферное давление 746 мм ртутного столба, фаза луны – первая четверть (39%), геомагнитная обстановка – небольшие возмущения.

При подключении прибора измерения значения в течение нескольких секунд возрастали до 208 мв, а затем начинали уменьшаться. В течение 12 часов измеряемое напряжение монотонно убывало до 100 мв.

При закреплении на дне сосуда биоэнергоструктуризатора БЭСТ-4м8 (стрелкой на север, картинкой вверх) измеряемое напряжение на электродах начинало возрастать. Измерительное устройство подключалось на три секунды, фиксировались максимальные значения.

Данные измерений приводятся в таблице и на графике.

Таким образом, за 12 часов разность потенциалов на электродах увеличилась в 1,74 раза. Практически во столько же раз возрос и ток проводимости, измеряемый гальванометром.

По такой же методике производились измерения разности потенциалов на электродах для питьевой воды 1 класса «Родничок». Данные измерений приводятся на графике ниже.

За 3 часа 20 минут разность потенциалов на электродах увеличилась в 2 раза. При дальнейших измерениях разность потенциалов на электродах начала падать и на третьи сутки составила 0,6 вольта за счет выпадения в осадок минеральных примесей воды.

На наш взгляд, приведенные результаты подтверждают гипотезу Эмилио дель Джудичи о способности когерентных доменов воды становится источником электродвижущей силы и способности БЭСТ-4м8 превращать воду в когерентные домены.

Есть данные, что когерентные домены воды увеличиваются в размере при воздействии на них определенных частот электромагнитного излучения.

Но, рассматриваемая гипотеза не отвечает на вопрос о структуре воды и ее свойстве повышать свою вязкость…

Если рассматривать когерентные домены, как наночастицы, то они должны проявлять себя как мелкие частицы вещества! Давайте вспомним опыты позапрошлого века Хладни, в которых мелкие частицы, помещенные на упругое основание, под действием звуковых частот образуют рисунки и форма их определяется формой основания и частотой воздействующих на них стоячих волн. При этом частицы скапливаются в узлах, где амплитуда стоячей волны нулевая, а в зоне максимальной амплитуды волны частицы рассеиваются.

Возникает вопрос, а не ведут ли себя также когерентные домены воды под действием стоячих волн электромагнитного излучения? Эта гипотеза позволяет объяснить образование любых форм квазикристаллов воды, но это вопрос дальнейших исследований свойств воды…

Сайт - www.biostim.narod.ru.

www.o8ode.ru

Что значит когерентность - Значения слов

может изменяться в пределах от A1 + А2 до А1 ≈ А2 в зависимости от разности фаз j1 ≈ j2 (). Интенсивность результирующего колебания, пропорциональная Ар2 также зависит от разности фаз.

В действительности идеально гармонические колебания неосуществимы, так как в реальных колебательных процессах амплитуда, частота и фаза колебаний непрерывно хаотически изменяются во времени. Результирующая амплитуда Ар существенно зависит от того, как быстро изменяется разность фаз. Если эти изменения столь быстры, что не могут быть замечены прибором, то измерить можно только среднюю амплитуду результирующего колебания . При этом, т.к. среднее значение cos (j1≈j2) равно 0, средняя интенсивность суммарного колебания равна сумме средних интенсивностей исходных колебаний: ═и, таким образом, не зависит от их фаз. Исходные колебания являются некогерентными. Хаотические быстрые изменения амплитуды также нарушают К. .

Если же фазы колебаний j1 и j2 изменяются, но их разность j1 ≈ j2 остается постоянной, то интенсивность суммарного колебания, как в случае идеально гармонических колебаний, определяется разностью фаз складываемых колебаний, то есть имеет место К. Если разность фаз двух колебаний изменяется очень медленно, то говорят, что колебания остаются когерентными в течение некоторого времени, пока их разность фаз не успела измениться на величину, сравнимую с p.

Можно сравнить фазы одного и того же колебания в разные моменты времени t1 и t2, разделённые интервалом t. Если негармоничность колебания проявляется в беспорядочном, случайном изменении во времени его фазы, то при достаточно большом t изменение фазы колебания может превысить p. Это означает, что через время t гармоническое колебание «забывает» свою первоначальную фазу и становится некогерентным «само себе». Время t называется временем К. негармонического колебания, или продолжительностью гармонического цуга. По истечении одного гармонического цуга он как бы заменяется другим с той же частотой, но др. фазой.

При распространении плоской монохроматической электромагнитной волны в однородной среде напряжённость электрического поля Е вдоль направления распространения этой волны ох в момент времени t равна:

═(

где l = сТ≈ длина волны, с ≈ скорость её распространения, Т ≈ период колебаний. Фаза колебаний в какой-нибудь определённой точке пространства сохраняется только в течение времени К. т. За это время волна распространится на расстояние сt и колебания Е в точках, удалённых друг от друга на расстояние сt, вдоль направления распространения волны, оказываются некогерентными. Расстояние, равное сt вдоль направления распространения плоской волны на котором случайные изменения фазы колебаний достигают величины, сравнимой с p, называют длиной К., или длиной цуга.

Видимый солнечный свет, занимающий на шкале частот электромагнитных волн диапазон от 4Ч1014 до 8Ч1014гц, можно рассматривать как гармоническую волну с быстро меняющимися амплитудой, частотой и фазой. При этом длина цуга ~ 10≈4 см. Свет, излучаемый разреженным газом в виде узких спектральных линий более близок к монохроматическому. Фаза такого света практически не меняется на расстоянии 10 см. Длина цуга лазерного излучения может превышать километры. В диапазоне радиоволн существуют более монохроматические источники колебаний (см. Кварцевый генератор , Квантовые стандарты частоты ), а длина волн l во много раз больше, чем для видимого света. Длина цуга радиоволн может значительно превышать размеры Солнечной системы.

Всё сказанное справедливо для плоской волны. Однако идеально плоская волна так же неосуществима, как и идеально гармоническое колебание (см. Волны ). В реальных волновых процессах амплитуды и фаза колебаний изменяются не только вдоль направления распространения волны, но и в плоскости, перпендикулярной этому направлению. Случайные изменения разности фаз в двух точках, расположенных в этой плоскости, увеличиваются с увеличением расстояния между ними. К. колебаний в этих точках ослабевает и на некотором расстоянии l, когда случайные изменения разности фаз становятся сравнимыми с p, исчезают. Для описания когерентных свойств волны, в плоскости, перпендикулярной направлению ее распространения, применяют термин пространственная К., в отличие от временной К., связанной со степенью монохроматичности волны. Все пространство, занимаемое волной, можно разбить на области, в каждой из которых волна сохраняет К. Объём такой области (объём К.) приблизительно равен произведению длины цуга сt на площадь круга диаметром / (размер пространственной К.).

Нарушение пространственной К. связано с особенностями процессов излучения и формирования волн. Например, пространственная К. световой волны, излучаемой протяжённым нагретым телом, исчезает на расстоянии от его поверхности всего в несколько длин волн, т.к. разные части нагретого тела излучают независимо друг от друга (см. Спонтанное излучение ). В результате вместо одной плоской волны источник излучает совокупность плоских волн, распространяющихся по всем возможным направлениям. По мере удаления от теплового источника (конечных размеров), волна все больше и больше приближается к плоской. Размер пространственной К. l растет пропорционально l ═≈ где R ≈ расстояние до источника, r ≈ размеры источника. Это позволяет наблюдать интерференцию света звёзд, несмотря на то, что они являются тепловыми источниками огромных размеров. Измеряя / для света от ближайших звёзд, удаётся определить их размеры r. Величину l/r называют углом К. С удалением от источника интенсивность света убывает как 1/R2. Поэтому с помощью нагретого тела нельзя получить интенсивное излучение, обладающее большой пространственной К.

Световая волна, излучаемая лазером , формируется в результате согласованного вынужденного излучения света во всем объеме активного вещества. Поэтому пространственная К. света у выходного отверстия лазера сохраняется во всем поперечном сечении луча. Лазерное излучение обладает огромной пространственной К., т. е. высокой направленностью по сравнению с излучением нагретого тела. С помощью лазера удаётся получить свет, объём К. которого в 1017 раз превышает объём К. световой волны той же интенсивности, полученной от наиболее монохроматических нелазерных источников света.

В оптике наиболее распространённым способом получения двух когерентных волн является расщепление волны, излучаемой одним немонохроматическим источником, на две волны, распространяющиеся по разным путям, но, в конце концов, встречающихся в одной точке, где и происходит их сложение (рис. 2). Если запаздывание одной волны по отношению к другой, связанное с разностью пройденных ими путей, меньше продолжительности цуга, то колебания в точке сложения будут когерентными и будет наблюдаться интерференция света. Когда разность путей двух волн приближается к длине цуга, К. лучей ослабевает. Колебания освещённости экрана уменьшаются, освещённость I стремится к постоянной величине, равной сумме интенсивностей двух волн, падающих на экран. В случае неточечного (протяжённого) теплового источника два луча, пришедшие в точки А и В, могут оказаться некогерентными из-за пространственной некогерентности излучаемой волны. В этом случае интерференция не наблюдается, так как интерференционные полосы от разных точек источника смещены относительно друг друга на расстояние, большее ширины полосы.

Понятие К., возникшее первоначально в классической теории колебаний и волн, применяется также по отношению к объектам и процессам, описываемым квантовой механикой (атомные частицы, твёрдые тела и т.д.).

Лит.: Ландсберг Г. С., Оптика, 4 изд., М., 1957; Горелик Г. С., Колебания и волны, 2 изд., М., 1959; Фабрикант В. А., Новое о когерентности, «Физика в школе», 1968, ╧ 1; Франсон М., Сланский С., Когерентность в оптике, пер. с франц., М., 1968; Мартинсен В., Шпиллер Е., Что такое когерентность, «Природа», 1968, ╧ 10.

А. В. Францессон.

xn--b1algemdcsb.xn--p1ai

Творческое объединение авторов и разработчиков «БИОСТИМ» - 13 Марта 2012

ТОАиР "БИОСТИМ"

О воде в наше время не писал разве только ленивый… На сайте «Все о воде» (http://www.o8ode.ru/) опубликовано более 1000 работ. Среди этих работ есть замечательная обзорная статья к.х.н. О.В. Мосина «Современная модель воды» (http://www.o8ode.ru/article/water/), в которой рассматриваются практически все гипотезы образования квазикристаллических структур в воде. Эти гипотезы объясняют образование из молекул воды различных структур, но не дают физического объяснения одного широко известного факта – повышенной электропроводности структурированной воды.

Ответ на это вопрос можно найти в гипотезе когерентных доменов (КД) профессора Миланского университета Эмилио дель Джудиче (Emilio Del Giudice), которая стала широко известна в 2007 года русскоязычному читателю после публикации перевода его лекции на 7-й Летней школе «Биофотоника и приложения биофотонов» (http://medscience.asia/articles/kogerentnaya-kvantovo-elektrodinamicheskaya-organizatsiya-biokhimicheskikh-protsessov

Согласно этой гипотезы в возбужденном состоянии многие электроны в молекулах воды почти свободны, и требуется совсем немного энергии, чтобы они стали полностью свободными. С позиций электрохимии можно сказать, что в некогерентном состоянии молекулы воды не могут выступать в качестве восстановителей — доноров электронов, а когерентная вода — хороший восстановитель. Более того, некогерентная вода удерживает электроны столь прочно, что может рассматриваться даже как мягкий окислитель, потому что ее молекула может удержать еще один электрон, превратившись в ион Н2О?, тогда как в когерентном состоянии вода легко отдает электроны, превращаясь в ионы Н2О. Поэтому если бы удалось разделить когерентную и некогерентную воду, то возникла бы электрическая батарея и возможность получения электродвижущей силы. Но обычная вода к этому неспособна, потому что обе фазы — некогерентная и когерентная — смешаны друг с другом, правда, на микроскопическом уровне эксперимент мог бы получиться.

Прибор измерения – цифровой мультиметр DT-830B в режиме измерения напряжения со шкалой 0 – 2000 mV.