Содержание
Масса литра холодной воды и литра кипятка одинакова
Казалось бы, что по-другому и быть не может — вода в чайнике до и после нагрева весит совершенно одинаково. И у нас есть все основания так думать, ведь на практике мы никогда не сталкивались с тем, что горячая вода оказывалась тяжелее холодной.
Но если вспомнить выведенную Эйнштейном взаимосвязь энергии и материи (выражаемую знаменитой формулой Е = тс2), то становится очевидным, что горячая вода должна быть тяжелее холодной!
Эта простая формула выражает всю суть так называемой концепции эквивалентности массы и энергии, гласящей, что масса тела — лишь мера внутренней энергии, запасенной в этом самом теле. И здесь совершенно не важна природа тела, из какого вещества оно состоит и в каком состоянии находится. В одном грамме абсолютно любой материи — будь то кусок дерева или металла, воздух или вода, да даже сам человек — содержится одно и то же количество энергии.
Понятие энергии здесь весьма абстрактно, и из самой формулы невозможно понять всю грандиозность закона, открытого Эйнштейном.
Если перевести энергию, запасенную в одном грамме любого вещества, в абсолютные величины, то откроется интересная и удивительная картина. Один грамм материи — это 21 кило-тонна в тротиловом эквиваленте, что примерно соответствует мощностям ядерных бомб, сброшенных 6 и 9 августа 1945 года на японские города Хиросима и Нагасаки. А 4 килограмма вещества содержат столько же энергии, сколько за год вырабатывает крупнейшая в мире гидроэлектростанция «Три ущелья», построенная в Китае на реке Янцзы. Если бы человечество научилось полностью использовать внутреннюю энергию материи, то можно было бы не думать о пресловутом «энергетическом голоде».
Но формула Е = тс2 не только говорит об эквивалентности энергии и массы, но и приводит к другим интересным выводам. Например, если каким-либо способом увеличить энергию тела, то и масса этого тела должна стать больше. Разгон тела или разогрев — вот самые простые средства добиться увеличения количества энергии, которая, прибавившись к энергии покоя, вызовет эквивалентное увеличение массы.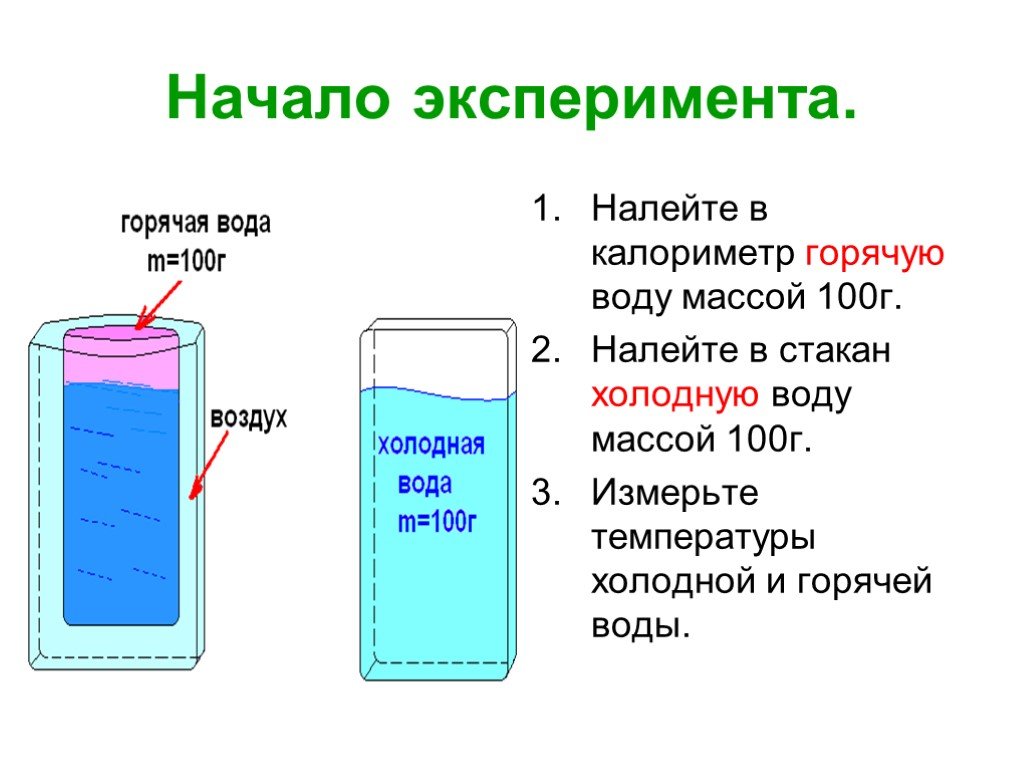
Так насколько потяжелеет литр воды при нагреве от 0 до 100 °С? Ненамного, потому что такой нагрев не связан с большими энергетическими затратами — увеличение массы не будет обнаружено даже самыми чувствительными приборами. А вот тонна воды уже даст показатель, находящийся на грани инструментальной погрешности, — 1000 кг воды, доведенные до кипения, станут тяжелее всего на пять миллионных долей грамма!
Энергии, с которыми мы имеем дело в повседневной жизни, не дают заметных следствий из закона Е = тс2. А вот физики, работающие с элементарными частицами и ускорителями, пользуются данной формулой ежедневно. Частицы, разогнанные до высоких скоростей, могут значительно прибавлять в массе. В частности, электрон, достигший скорости в 299 800 км/с (почти скорости света), становится в 20 раз тяжелее!
Да, в обычной жизни мы можем говорить об одинаковой массе литра холодной воды и литра кипятка, однако, с физической точки зрения, это неверно — любое изменение количества энергии в теле неизбежно ведет и к изменению его массы.
Простая формула Е = тс2 за свое вековое существование еще ни разу не подвела.
Предыдущая статья: Ни одного органа
Следующая статья: Чем больше напряжение электрического тока, тем он опаснее для человека
Лабораторная работа №1. Сравнение количеств теплоты при смешивании воды разной температуры.
Сравнение количеств теплоты при смешивании воды разной температуры.
Цель работы: определить количество теплоты, отданное горячей водой и полученное холодной при теплообмене. Объяснить полученный результат.
Из учебника мы знаем, что при теплопередаче происходит переход энергии от одних тел к другим путем теплопроводности, излучения или конвекции. Энергия, которую получает или отдает тело при теплопередаче, называется количеством теплоты. Мы знаем также, что количество теплоты, необходимое для нагревания тела (или выделяемое им при остывании), зависит от рода вещества, из которого оно состоит, от массы этого тела и от изменения его температуры.
Итак, понятно, что в процессе теплопередачи между двумя телами их температуры стремятся уравняться. Тело с более высокой температурой отдает некоторое количество теплоты, а тело с более низкой температурой получает это количество теплоты. Причем в идеальных условиях, когда два этих тела абсолютно изолированы от всего на свете, переданное количество теплоты должно быть равно полученному согласно закону сохранения энергии.
Однако, условия проводимого нами эксперимента безусловно далеки от идеальных. От горячей воды тепло передается не только холодной воде, но и калориметру, термометру, окружающему воздуху. Тем не менее, хотя мы и не получим входе эксперимента полного соответствия отданного количества теплоты полученному, эти показатели, если эксперимент выполнен аккуратно, должны быть близки. Ход работы описан в учебнике.
Пример выполнения работы.
Вычисления:
Количество теплоты, отданное горячей водой — 12600Дж.
Количество теплоты, полученное холодной водой — 10920Дж.
Вывод: Количество теплоты, полученное холодной водой близко к количеству теплоты, отданному горячей водой, что, с учетом далеких от идеальных условий эксперимента, можно считать равенством.
1) Как определялась в эксперименте масса воды?
Через плотность по формуле m=pV, т.е. косвенно, без использования весов. Так как плотность воды 1 г/см3, то масса 100 мл = 100 см3 будет 100г = 0,1 кг
2) Почему калориметр имеет двойные стенки?
Чтобы меньше терялась теплота в окружающую среду
3) Почему холодную воду надо брать комнатной температуры?
Чтобы её температура не изменялась из-за влияния воздуха в кабинете, т.к. она же не в калориметре
4) Будут ли равными изменения температуры и количество отданной и принятой теплоты, если использовать неравные массы теплой и холодной воды?
Изменения температуры не будут одинаковыми, а количество отданной и принятой теплоты будут равны
Суперзадание: объясните, как влияет на полученные результаты участие в теплообмене калориметра.
Всегда ли можно этим влиянием пренебречь?
Ответ: Уравнение теплового баланса строго выполняется только в том случае, если система теплоизолирована. Хотя калориметр снижает потери энергии, связанные с теплопередачей в окружающую среду, тем не менее они остаются. Кроме того, есть потери за счёт теплообмена между водой и калориметром. Поэтому количество теплоты, одданное теплой водой, будет всегда больше, чем количество теплоты, полученное холодной водой. Если тёплую воду вливать в холодную, то различие между Qотд и Qпол будет больше, чем в случае, когда холодную воду добавляют в тёплую. Это обусловлено тем, что в первом случае потери энергии в окружающую среду будут частично скомпенсированы за счёт количества теплоты, которое холодной воде передают калориметр и термометр.
Таким образом, как это ни кажется странным, проверяемое положение о равенстве отданного и принятого количества теплоты выполнения работы будет подтверждено точнее, если в калориметр наливать сначала холодную воду, а затем доливать горячую (как и указано в работе).
Что касается второй части вопросы, всегда ли можно влиянием калориметра пренебречь? Нет, не в сегда. Можно пренебречь тогда, когда удельная теплоёмкость и масса внутреннего стакана калориметра мала по сравнению с массой воды (жидкости) находящейся в калориметре.
Источник:
Решебник
по
физике
за 8 класс (А.В.Перышкин, Н.А.Родина, 1998 год),
задача №1
к главе «Лабораторные работы».
Все задачи
← Введение
Лабораторная работа №2. Измерение удельной теплоемкости твердого тела. →
Как рассчитать постоянную калориметра
Как рассчитать постоянную калориметра
Как рассчитать постоянную калориметра
Назад в меню термохимии
Решите две письменные задачи
Сделай два видео бок о бок
Решите еще две задачи
Пример #1: Когда 40,0 мл воды при 60,0 °C добавляют к 40,0 мл воды при 25,0 °C, уже находящейся в калориметре, температура повышается на 15,0 °C.
Что такое постоянная калориметра?
Решение:
Необходимо найти разницу между теплотой, отдаваемой горячей водой при понижении ее температуры с 60,0 до 40,0, и теплотой, приобретаемой холодной водой при ее нагревании до 40,0 с 25,0. Обратите внимание, что значения в задаче указаны в мл, а значения в решении — в граммах. Объем (мл) преобразуется в массу (граммы) с использованием плотности воды (1,00 г/мл).
1) Потери горячей воды:
q = m Δt C p
q = (40,0 г) (20,0 °C) (4,184 Дж г¯ 1 °С¯ 1 )
q = 3347,2 Дж
2) Холодная вода досталась:
q = m Δt C p
q = (40,0 г) (15,0 °C) (4,184 Дж г¯ 1 °C¯ 1 )
q = 2510,4 Дж
3) Остальное досталось калориметру:
3347,2 − 2510,4 = 836,8 Дж
4) Найдите теплоемкость калориметра:
836,8 Дж / 15,0 °С = 55,8 Дж / °С
Пример #2: Рассчитайте постоянную калориметра, если 25,0 г воды при 60,0 °C добавить к 25,0 г воды при 25,0 °C, получив при этом температуру 35,0 °C?
Решение:
Если бы константа была равна нулю, конечная температура воды была бы 42,5 °C.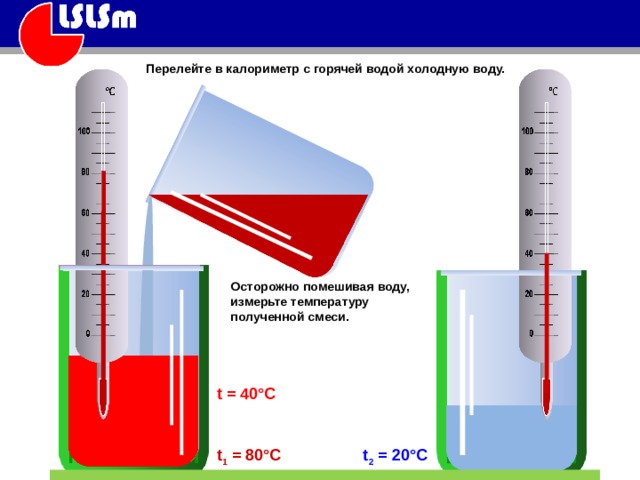
Таким образом, количество тепла, используемого калориметром для нагревания с 25 до 35, равно:
(25,0) (4,184) (7,5) = 784,5 Дж.
Поскольку константа равна джоулю/градусу, константа равна
784,5 Дж / 10,0 °C = 78,4 Дж/°C (с точностью до трех знаков).
Определение постоянной калориметра I
Определение постоянной калориметра II
Пример #3: Калориметр должен быть откалиброван: 72,55 г воды при 71,6 °C добавляют в калориметр, содержащий 58,85 г воды при 22,4 °C. После перемешивания и ожидания уравновешивания системы конечная температура достигла 47,3°С. Рассчитайте теплоемкость калориметра. (Удельная теплоемкость воды 4,184 Дж/г¯ 1 °С¯ 1 ).
Решение:
1) Потери энергии с горячей водой:
q = м С p ΔT
q = (72,55 г) (4,184 Дж г¯ 1 °C¯ 1 ) (24,3 °C)
q = 7376,24 Дж
2) Энергия, получаемая холодной водой:
q = м С p ΔT
q = (58,85 г) (4,184 Дж г¯ 1 °C¯ 1 ) (24,9 °C)
q = 5818,54 Дж
3) Остальное досталось калориметру:
7376,24 − 5818,54 = 1557,7 Дж
4) Теплоемкость калориметра:
1557,7 Дж / 24,9°С = 62,6 Дж/°С
Пример #4: Студент хочет определить теплоемкость калориметра кофейной чашки.
После смешивания 100,0 г воды при 58,5 °С со 100,0 г воды уже в калориметре при 22,8 °С конечная температура воды составляет 39,7 °С. Рассчитайте теплоемкость калориметра в Дж/°С. (В качестве удельной теплоемкости воды используйте 4,184 Дж г¯ 1 °C¯ 1 .)
Решение:
1) Теплота, отдаваемая теплой водой:
q = (100,0 г) (18,8 °С) (4,184 Дж г¯ 1 °С¯ 1 ) = 7865,92 Дж
2) Теплота, поглощаемая водой в калориметре:
q = (100,0 г) (16,9 °С) (4,184 Дж/г °С) = 7070,96 Дж
3) Разница поглотилась калориметром:
7865,92 − 7070,96 = 794,96 Дж
4) Постоянная калориметра:
794,96 Дж / 16,9°С = 47,0 Дж/°С
Назад в меню термохимии
Горячая и холодная вода | Фургон физики
Категория
Выберите категориюО фургоне физикиЭлектричество и магнитыВсе остальноеСвет и звукДвижение вещейНовая и захватывающая физикаСостояния материи и энергииКосмосПод водой и в воздухе
Подкатегория
Поиск
Задайте вопрос
Последний ответ: 22.
10.2007
Q:
Содержит ли горячая и холодная вода одинаковое количество молекул? Они одинаковы?
— Комната 15
Lusher School, Сент-Луис, Миссури
A:
На количество молекул в воде не влияет изменение ее температуры. Но чтобы узнать, есть ли у вас одинаковое количество молекул в двух образцах воды, вам нужно сравнить их массы, а не объемы. Когда вы нагреваете холодную воду, она расширяется. (Когда вы немного нагреваете ледяную воду, она немного сжимается, но давайте не будем усложнять.) Итак, горячая вода занимает больше места, чем холодная. Количество места, которое что-то занимает, называется объемом. Если бы у вас было 2 стакана воды, один с горячей водой и один с холодной водой с равными объемами, в холодной воде было бы больше молекул.
Горячая и холодная вода состоят из молекул одного и того же типа. Каждая молекула имеет один атом кислорода и два атома водорода. Разница между ними заключается в скорости движения молекул.
Джейсон (с Майком)
(опубликовано 22.10.2007)
Дополнение №1: изменение объема воды при нагревании
В:
почему молекулы в холодной воде сжаты сильнее, чем в теплой?
— Джерри Энн Мари Табинь (13 лет)
maramag bukidnon mindanao, philippines
A:
Когда вода горячая, молекулы вращаются быстрее. Они не проводят так много времени, тесно прижавшись друг к другу, и проводят больше времени немного порознь. Так они занимают больше места.
Однако вода необычна, поскольку при охлаждении ниже 4°C она начинает расширяться при дальнейшем охлаждении. Бывает, что есть особый способ, которым молекулы могут хорошо стыковаться друг с другом (с низкой энергией), который размещает их немного дальше друг от друга, чем большинство способов стыковки почти так же хорошо. Когда вода превращается в лед, молекулы выстраиваются особым образом, и лед занимает больше места, чем жидкость.
Майк В.
(опубликовано 05.03.2011)
Дополнение №2: зачем стирать в теплой воде?
Q:
Я понимаю, что холодная и теплая вода почти одинаковы с точки зрения объема и молекул и т. д. Так почему же мы должны мыть руки теплой водой, а не холодной? Какая разница?
— Кэти (12 лет)
Уиллистон, Вермонт, США
A:
Хотя холодная и теплая вода очень похожи, в некоторых случаях температура имеет большое значение. Многие материалы лучше растворяются в горячей воде, чем в холодной. Основная причина заключается в том, что часто требуется некоторая энергия, чтобы оторвать молекулу от других подобных молекул и превратить ее в воду. Чем жарче вещи, тем чаще вы получаете столько энергии. Кроме того, химические процессы (в том числе растворение) почти всегда происходят быстрее при высокой температуре. Часто для того, чтобы молекула могла перемещаться из одного места в другое или из одной формы в другую, она должна пройти через состояние с более высокой энергией, подобно тому, как она преодолевает небольшую неровность.
Опять же, чем жарче вещи, тем чаще это происходит.
Майк В.
(опубликовано 05.03.2011)
Дополнение № 3: Плотнее ли горячая вода льда?
Q:
Правильно ли я сказал, что вода занимает больше объема при высокой температуре (пример: 60C), когда она охлаждается до 5C, она занимает меньше места, а после этого, когда она замерзает, она снова занимает больше объема? Если да, имел ли он равный объем в какой-то момент между объемом замерзшей воды и сравнил, когда она горячая?
— Джин (15 лет)
Монреаль, Канада
A:
Как оказалось, плотность жидкой воды (при давлении в одну атмосферу) при 100°C падает всего на 4,2% ниже плотности при 4°C. Плотность льда падает примерно на 9% ниже этого значения. Таким образом, лед занимает больший объем, чем жидкость во всем этом диапазоне.
Майк В.
(опубликовано 14.09.2011)
Дополнение к этому ответу
Похожие вопросы
теплоизоляция
ГОРЯЧАЯ ВОМНАЯ ДЛЯ СОХРАНЯЯ СЛАДКИ
Тепловая вместимость при постоянном объеме или давлении
Сохранение молока
.
90 обратимая теплопередача?
