Справочник химика 21. Энтальпия воды

Энтальпия - это... Что такое Энтальпия?

Энтальпи́я, также тепловая функция и теплосодержание — термодинамический потенциал, характеризующий состояние системы в термодинамическом равновесии при выборе в качестве независимых переменных давления, энтропии и числа частиц.

Проще говоря, энтальпия — это та энергия, которая доступна для преобразования в теплоту при определенных температуре и давлении.

Если термомеханическую систему рассматривать как состоящую из макротела (газа) и поршня площадью S с грузом весом Р = pS, уравновешивающего давление газа р внутри сосуда, то такая система называется расширенной.

Энтальпия или энергия расширенной системы Е равна сумме внутренней энергии газа U и потенциальной энергии поршня с грузом Eпот = pSx = pV

Таким образом, энтальпия в данном состоянии представляет собой сумму внутренней энергии тела и работы, которую необходимо затратить, чтобы тело объёмом V ввести в окружающую среду, имеющую давление р и находящуюся с телом в равновесном состоянии. Энтальпия системы H — аналогично внутренней энергии и другим термодинамическим потенциалам — имеет вполне определенное значение для каждого состояния, т. е. является функцией состояния. Следовательно, в процессе изменения состояния

$\Delta H=H_2-H_1$

Изменение энтальпии (или Тепловой эффект химической реакции) не зависит от пути процесса, определяясь только начальным и конечным состоянием системы. Если система каким-либо путём возвращается в исходное состояние (круговой процесс), то изменение любого её параметра, являющегося функцией состояния, равно нулю, отсюда $\Delta H=0$ , или же

$\oint \delta H =0$

Дифференциал энтальпии, выраженный в собственных переменных — через энтропию S и давление p:

$\begin{align} \mathrm{d}H &= \mathrm{d}(U+ pV) \\ &= \mathrm{d}U+\mathrm{d}(pV) \\ &= \mathrm{d}U+(p\,\mathrm{d}V+V\,\mathrm{d}p) \\ &= (\delta Q-p\,\mathrm{d}V)+(p\,\mathrm{d}V+V\,\mathrm{d}p) \\ &= \delta Q+V\,\mathrm{d}p \\ &= T\,\mathrm{d}S+V\,\mathrm{d}p \end{align}$

Поскольку в квазиравновесных процессах $T\, \mathrm{d}S = \delta Q$ — количество теплоты, подведенной к системе, отсюда вытекает физический смысл введения понятия энтальпии: ее изменение — это тепло, подведенное к системе в изобарическом процессе (при постоянном давлении). Практическое применение этой функции основано на том, что множество химических процессов в реальных или лабораторных условиях реализуются именно при постоянном (атмосферном) давлении, когда резервуар открыт. Так, энтальпия образования — количество энергии, которое выделяется или поглощается при образовании сложного вещества из простых веществ.

Все химические реакции сопровождаются выделением (экзотермические) или поглощением (эндотермические) тепла. Мерой теплоты реакции служит изменение энтальпии ΔН, которая соответствует теплообмену при постоянном давлении. В случае экзотермических реакций система теряет тепло и ΔН — величина отрицательная. В случае эндотермических реакций система поглощает тепло и ΔН — величина положительная.

Энтальпией системы удобно пользоваться в тех случаях, когда в качестве независимых переменных, определяющих состояние системы, выбирают давление р и температуру Т

В этом случае изменение энтальпии в изобарическом процессе практически удобно рассчитывать, зная теплоемкость при постоянном давлении C_p(T) (термохимический закон Кирхгофа): $\Delta H (T_1 \to T_2) (p=\mathrm{const}) = \int\delta Q = \int\limits_{T_1}^{T_2} C_p(T) \mathrm{d} T$

При этом используется эмпирическое разложение теплоёмкости в ряд по степеням Т:

$C_p(T)= \sum a_i*T^i$

Энтальпия — величина аддитивная (экстенсивная), т. е. для сложной системы равна сумме энтальпий её независимых частей $H=\sum H_i$ . Подобно другим термодинамическим потенциалам, энтальпия определяется с точностью до постоянного слагаемого, которому в термодинамике часто придают произвольные значения (например, при расчете и построении тепловых диаграмм). При наличии немеханических сил величина энтальпии системы равна

$H = U + pV - \sum X_iy_i$

где X_i — обобщённая сила; y_i — обобщённая координата.

Примеры

Инвариантная энтальпия в релятивистской термодинамике

При построении релятивистской термодинамики (с учетом специальной теории относительности) обычно наиболее удобным подходом является использование так называемой инвариантной энтальпии — для системы, находящейся в некотором сосуде.

При этом подходе температура определяется как лоренц-инвариант. Энтропия — также инвариант. Поскольку стенки влияют на систему, наиболее естественной независимой переменной является давление , в связи с чем в качестве термодинамического потенциала удобно брать именно энтальпию[1].

Для такой системы «обычная» энтальпия и импульс системы $\vec g$ образуют 4-вектор, и за определение инвариантной энтальпии, одинаковой во всех системах отсчёта, берётся инвариантная функция этого 4-вектора:

$H=\sqrt{\left(U+P \,V \right)^2 -c^2 \vec g^2}$

Основное уравнение релятивистской термодинамики записывается через дифференциал инвариантной энтальпии следующим образом:

$dH=T \, dS +\frac{V}{\sqrt{1-v^2/c^2}}\, dP + \mu\, dN$

Пользуясь этим уравнением, можно решить любой вопрос термодинамики движущихся систем, если известна функция H(S,P,N) .

См. также

Источники

Болгарский А. В., Мухачев Г. А., Щукин В. К., «Термодинамика и теплопередача» Изд. 2-е, перераб. и доп. М.: «Высшая школа», 1975, 495 с.
Харин А. Н., Катаева Н. А., Харина Л. Т., под ред. проф. Харина А. Н. «Курс химии», М.: «Высшая школа», 1975, 416 с.

Примечания

dic.academic.ru

Энтальпия

Определением этой величины служит тождество: H=U+PV

Размерность энтальпии-Дж/моль.

В химии чаще всего рассматривают изобарические процессы (P = const), и тепловой эффект в этом случае называют изменением энтальпии системы или энтальпией процесса:

В термодинамической системе выделяющуюся теплоту химического процесса условились считать отрицательной (экзотермический процесс, ΔH < 0), а поглощение системой теплоты соответствует эндотермическому процессу, ΔH > 0.

Энтропия

Основное содержание второго начала термодинамики заключается в постулировании существования функции, называемой энтропией S, которая для обратимых процессов определяется по уравнению

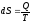
а для самопроизвольных

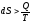
Изменение энтропии реакции можно рассчитать по формуле

Зависимость изменения энтропии от температуры выражается законом Кирхгофа:

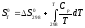
Для изолированной системы изменение энтропии – критерий возможности самопроизвольного протекания процесса. Если , то процесс возможен; если, то в прямом направлении процесс невозможен; если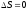, то в системе равновесие.

Термодинамические потенциалы. Свободная энергия Гиббса и Гельмгольца.

Дл я характеристики процессов, протекающих в закрытых системах, введем новые термодинамические функции состояния: изобарно-изотермический потенциал (свободная энергия Гиббса G) и изохорно-изотермический потенциал (свободная энергия Гельмгольца F).

Для закрытой системы, в которой осуществляется равновесный процесс при постоянных температуре и объеме, выразим работу данного процесса. Которую обозначим Аmax (посколько работа процесса, проводимого равновесно, максимальна):

Amax=T∆S-∆U

Введем функцию F=U-TS-изохорно-изотермический потенциал, определяющий направление и предел самопроизвольного протекания процесса в закрытой системе, находящейся в изохорно-изотермических условиях и получим:

∆F=∆U-T∆S

Изменение энергии Гельмгольца определяется только начальным и конечным состоянием системы и не зависит от характера процесса, поскольку оно определяется двумя функциями состояния: U и S. Напомним, что от способа проведения процесса при переходе системы из начального в конечное состояние может зависеть величина полученной или затраченной работы, но не изменение функции.

Закрытую систему, находящуюся в изобарно- изотермических условиях, характеризует изобарно-изотермический потенциал G:

G=U+PV-TS=H-TS

∆G=∆H-T∆S

Дифференциалэнергии Гиббса для системы с постоянным числом частиц, выраженный в собственных переменных — черездавлениеp итемпературуT:

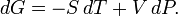
Для системы с переменным числом частиц этот дифференциал записывается так:

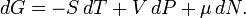
Здесь 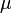—химический потенциал, который можно определить как энергию, которую необходимо затратить, чтобы добавить в систему ещё одну частицу.

Анализ уравнения ∆G=∆H-T∆S позволяет установить, какой из факторов, составляющих энергию Гиббса, ответственен за направление протекания химической реакции, энтальпийный (ΔH) или энтропийный (ΔS · T).

Если ΔH < 0 и ΔS > 0, то всегда ΔG < 0 и реакция возможна при любой температуре.

Если ΔH > 0 и ΔS < 0, то всегда ΔG > 0, и реакция с поглощением теплоты и уменьшением энтропии невозможна ни при каких условиях.

В остальных случаях (ΔH < 0, ΔS < 0 и ΔH > 0, ΔS > 0) знак ΔG зависит от соотношения ΔH и TΔS. Реакция возможна, если она сопровождается уменьшением изобарного потенциала; при комнатной температуре, когда значение T невелико, значение TΔS также невелико, и обычно изменение энтальпии больше TΔS. Поэтому большинство реакций, протекающих при комнатной температуре, экзотермичны. Чем выше температура, тем больше TΔS, и даже эндотермические реакции становятся осуществляемыми.

Под стандартной энергией Гиббса образования ΔG°, понимают изменение энергии Гиббса при реакции образования 1 моль вещества, находящегося в стандартном состоянии. Это определение подразумевает, что стандартная энергия Гиббса образования простого вещества, устойчивого в стандартных условиях, равна нулю.

Изменение энергии Гиббса не зависит от пути процесса, следовательно можно получать разные неизвестные значения энергий Гиббса образования из уравнений, в которых с одной стороны записанны суммы энергий продуктов реакции, а с другой - суммы энергий исходных веществ.

При пользовании значениями стандартной энергии Гиббса критерием принципиальной возможности процесса в нестандартных условиях принимается условие ΔG° < 0, а критерием принципиальной невозможности — условие ΔG° > 0. В то же время, если стандартная энергия Гиббса равна нулю, это не означает, что в реальных условиях (отличных от стандартных) система будет в равновесии.

Условия самопроизвольного протекания процессов в закрытый системах :

∆G<0, dG<0;

∆F<0,dF<0.

studfiles.net

Свойства насыщенного водяного пара от 0 до 100 бар. Давление насыщенного. Температура кипения (конденсации). Плотность. Объемная масса. Удельная энтальпия воды и пара. Удельная теплота парообразования. Теплоемкость и вязкость пара.

www.dpva.ru

Давление насыщенного пара (абсолютное)	Температура кипения (конденсации).	Удельный объем = объемная масса (обратная плотность)	Плотность. (пара)	Удельная энтальпия жидкой воды		Удельная энтальпия пара		Удельная теплота парообразования (конденсации)		Теплоемкость пара	Динамическая вязкость пара
бар	°C	м3/кг	кг/м3	кДж/кг	кКал/кг	кДж/кг	кКал/кг	кДж/кг	кКал/кг	кДж/(кг*°C)	кг/(м*с)
0.02	17.51	67.006	0.015	73.45	17.54	2533.64	605.15	2460.19	587.61	1.8644	0.000010
0.03	24.10	45.667	0.022	101.00	24.12	2545.64	608.02	2444.65	583.89	1.8694	0.000010
0.04	28.98	34.802	0.029	121.41	29.00	2554.51	610.13	2433.10	581.14	1.8736	0.000010
0.05	32.90	28.194	0.035	137.77	32.91	2561.59	611.83	2423.82	578.92	1.8774	0.000010
0.06	36.18	23.741	0.042	151.50	36.19	2567.51	613.24	2416.01	577.05	1.8808	0.000010
0.07	39.02	20.531	0.049	163.38	39.02	2572.62	614.46	2409.24	575.44	1.8840	0.000010
0.08	41.53	18.105	0.055	173.87	41.53	2577.11	615.53	2403.25	574.01	1.8871	0.000010
0.09	43.79	16.204	0.062	183.28	43.78	2581.14	616.49	2397.85	572.72	1.8899	0.000010
0.1	45.83	14.675	0.068	191.84	45.82	2584.78	617.36	2392.94	571.54	1.8927	0.000010
0.2	60.09	7.650	0.131	251.46	60.06	2609.86	623.35	2358.40	563.30	1.9156	0.000011
0.3	69.13	5.229	0.191	289.31	69.10	2625.43	627.07	2336.13	557.97	1.9343	0.000011
0.4	75.89	3.993	0.250	317.65	75.87	2636.88	629.81	2319.23	553.94	1.9506	0.000011
0.5	81.35	3.240	0.309	340.57	81.34	2645.99	631.98	2305.42	550.64	1.9654	0.000012
0.6	85.95	2.732	0.366	359.93	85.97	2653.57	633.79	2293.64	547.83	1.9790	0.000012
0.7	89.96	2.365	0.423	376.77	89.99	2660.07	635.35	2283.30	545.36	1.9919	0.000012
0.8	93.51	2.087	0.479	391.73	93.56	2665.77	636.71	2274.05	543.15	2.0040	0.000012
0.9	96.71	1.869	0.535	405.21	96.78	2670.85	637.92	2265.65	541.14	2.0156	0.000012
1	99.63	1.694	0.590	417.51	99.72	2675.43	639.02	2257.92	539.30	2.0267	0.000012
1.1	102.32	1.549	0.645	428.84	102.43	2679.61	640.01	2250.76	537.59	2.0373	0.000012
1.2	104.81	1.428	0.700	439.36	104.94	2683.44	640.93	2244.08	535.99	2.0476	0.000012
1.3	107.13	1.325	0.755	449.19	107.29	2686.98	641.77	2237.79	534.49	2.0576	0.000013
1.4	109.32	1.236	0.809	458.42	109.49	2690.28	642.56	2231.86	533.07	2.0673	0.000013
1.5	111.37	1.159	0.863	467.13	111.57	2693.36	643.30	2226.23	531.73	2.0768	0.000013
1.5	111.37	1.159	0.863	467.13	111.57	2693.36	643.30	2226.23	531.73	2.0768	0.000013
1.6	113.32	1.091	0.916	475.38	113.54	2696.25	643.99	2220.87	530.45	2.0860	0.000013
1.7	115.17	1.031	0.970	483.22	115.42	2698.97	644.64	2215.75	529.22	2.0950	0.000013
1.8	116.93	0.977	1.023	490.70	117.20	2701.54	645.25	2210.84	528.05	2.1037	0.000013
1.9	118.62	0.929	1.076	497.85	118.91	2703.98	645.83	2206.13	526.92	2.1124	0.000013
2	120.23	0.885	1.129	504.71	120.55	2706.29	646.39	2201.59	525.84	2.1208	0.000013
2.2	123.27	0.810	1.235	517.63	123.63	2710.60	647.42	2192.98	523.78	2.1372	0.000013
2.4	126.09	0.746	1.340	529.64	126.50	2714.55	648.36	2184.91	521.86	2.1531	0.000013
2.6	128.73	0.693	1.444	540.88	129.19	2718.17	649.22	2177.30	520.04	2.1685	0.000013
Давление насыщенного пара (абсолютное)	Температура кипения (конденсации).	Удельный объем = объемная масса (обратная плотность)	Плотность. (пара)	Удельная энтальпия жидкой воды		Удельная энтальпия пара		Удельная теплота парообразования (конденсации)		Теплоемкость пара	Динамическая вязкость пара
бар	°C	м3/кг	кг/м3	кДж/кг	кКал/кг	кДж/кг	кКал/кг	кДж/кг	кКал/кг	кДж/(кг*°C)	кг/(м*с)
2.8	131.20	0.646	1.548	551.45	131.71	2721.54	650.03	2170.08	518.32	2.1835	0.000013
3	133.54	0.606	1.651	561.44	134.10	2724.66	650.77	2163.22	516.68	2.1981	0.000013
3.5	138.87	0.524	1.908	584.28	139.55	2731.63	652.44	2147.35	512.89	2.2331	0.000014
4	143.63	0.462	2.163	604.68	144.43	2737.63	653.87	2132.95	509.45	2.2664	0.000014
4.5	147.92	0.414	2.417	623.17	148.84	2742.88	655.13	2119.71	506.29	2.2983	0.000014
5	151.85	0.375	2.669	640.12	152.89	2747.54	656.24	2107.42	503.35	2.3289	0.000014
5.5	155.47	0.342	2.920	655.81	156.64	2751.70	657.23	2095.90	500.60	2.3585	0.000014
6	158.84	0.315	3.170	670.43	160.13	2755.46	658.13	2085.03	498.00	2.3873	0.000014
6.5	161.99	0.292	3.419	684.14	163.40	2758.87	658.94	2074.73	495.54	2.4152	0.000014
7	164.96	0.273	3.667	697.07	166.49	2761.98	659.69	2064.92	493.20	2.4424	0.000015
7.5	167.76	0.255	3.915	709.30	169.41	2764.84	660.37	2055.53	490.96	2.4690	0.000015
8	170.42	0.240	4.162	720.94	172.19	2767.46	661.00	2046.53	488.80	2.4951	0.000015
8.5	172.94	0.227	4.409	732.03	174.84	2769.89	661.58	2037.86	486.73	2.5206	0.000015
9	175.36	0.215	4.655	742.64	177.38	2772.13	662.11	2029.49	484.74	2.5456	0.000015
9.5	177.67	0.204	4.901	752.82	179.81	2774.22	662.61	2021.40	482.80	2.5702	0.000015
10	179.88	0.194	5.147	762.60	182.14	2776.16	663.07	2013.56	480.93	2.5944	0.000015
11	184.06	0.177	5.638	781.11	186.57	2779.66	663.91	1998.55	477.35	2.6418	0.000015
12	187.96	0.163	6.127	798.42	190.70	2782.73	664.64	1984.31	473.94	2.6878	0.000015
13	191.60	0.151	6.617	814.68	194.58	2785.42	665.29	1970.73	470.70	2.7327	0.000015
14	195.04	0.141	7.106	830.05	198.26	2787.79	665.85	1957.73	467.60	2.7767	0.000016
15	198.28	0.132	7.596	844.64	201.74	2789.88	666.35	1945.24	464.61	2.8197	0.000016
16	201.37	0.124	8.085	858.54	205.06	2791.73	666.79	1933.19	461.74	2.8620	0.000016
17	204.30	0.117	8.575	871.82	208.23	2793.37	667.18	1921.55	458.95	2.9036	0.000016
18	207.11	0.110	9.065	884.55	211.27	2794.81	667.53	1910.27	456.26	2.9445	0.000016
19	209.79	0.105	9.556	896.78	214.19	2796.09	667.83	1899.31	453.64	2.9849	0.000016
20	212.37	0.100	10.047	908.56	217.01	2797.21	668.10	1888.65	451.10	3.0248	0.000016
21	214.85	0.095	10.539	919.93	219.72	2798.18	668.33	1878.25	448.61	3.0643	0.000016
22	217.24	0.091	11.032	930.92	222.35	2799.03	668.54	1868.11	446.19	3.1034	0.000016
23	219.55	0.087	11.525	941.57	224.89	2799.77	668.71	1858.20	443.82	3.1421	0.000016
24	221.78	0.083	12.020	951.90	227.36	2800.39	668.86	1848.49	441.50	3.1805	0.000017
Давление насыщенного пара (абсолютное)	Температура кипения (конденсации).	Удельный объем = объемная масса (обратная плотность)	Плотность. (пара)	Удельная энтальпия жидкой воды		Удельная энтальпия пара		Удельная теплота парообразования (конденсации)		Теплоемкость пара	Динамическая вязкость пара
бар	°C	м3/кг	кг/м3	кДж/кг	кКал/кг	кДж/кг	кКал/кг	кДж/кг	кКал/кг	кДж/(кг*°C)	кг/(м*с)
25	223.94	0.080	12.515	961.93	229.75	2800.91	668.99	1838.98	439.23	3.2187	0.000017
26	226.03	0.077	13.012	971.69	232.08	2801.35	669.09	1829.66	437.01	3.2567	0.000017
27	228.06	0.074	13.509	981.19	234.35	2801.69	669.17	1820.50	434.82	3.2944	0.000017
28	230.04	0.071	14.008	990.46	236.57	2801.96	669.24	1811.50	432.67	3.3320	0.000017
29	231.96	0.069	14.508	999.50	238.73	2802.15	669.28	1802.65	430.56	3.3695	0.000017
30	233.84	0.067	15.009	1008.33	240.84	2802.27	669.31	1793.94	428.48	3.4069	0.000017
30	233.84	0.067	15.009	1008.33	240.84	2802.27	669.31	1793.94	428.48	3.4069	0.000017
31	235.66	0.064	15.512	1016.97	242.90	2802.33	669.32	1785.36	426.43	3.4442	0.000017
32	237.44	0.062	16.016	1025.41	244.92	2802.32	669.32	1776.90	424.41	3.4815	0.000017
33	239.18	0.061	16.521	1033.69	246.89	2802.25	669.31	1768.56	422.41	3.5187	0.000017
34	240.88	0.059	17.028	1041.79	248.83	2802.12	669.28	1760.33	420.45	3.5559	0.000017
35	242.54	0.057	17.536	1049.74	250.73	2801.95	669.23	1752.20	418.51	3.5932	0.000017
36	244.16	0.055	18.046	1057.54	252.59	2801.72	669.18	1744.17	416.59	3.6305	0.000017
37	245.75	0.054	18.557	1065.21	254.42	2801.44	669.11	1736.24	414.69	3.6679	0.000017
38	247.31	0.052	19.070	1072.73	256.22	2801.12	669.04	1728.39	412.82	3.7054	0.000017
39	248.84	0.051	19.585	1080.13	257.98	2800.75	668.95	1720.62	410.96	3.7429	0.000018
40	250.33	0.050	20.101	1087.40	259.72	2800.34	668.85	1712.94	409.13	3.7806	0.000018
41	251.80	0.048	20.619	1094.56	261.43	2799.89	668.74	1705.33	407.31	3.8185	0.000018
42	253.24	0.047	21.138	1101.61	263.12	2799.40	668.62	1697.79	405.51	3.8565	0.000018
43	254.66	0.046	21.660	1108.55	264.77	2798.87	668.50	1690.32	403.73	3.8946	0.000018
44	256.05	0.045	22.183	1115.39	266.41	2798.30	668.36	1682.91	401.96	3.9329	0.000018
45	257.41	0.044	22.708	1122.13	268.02	2797.70	668.22	1675.57	400.20	3.9715	0.000018
46	258.76	0.043	23.235	1128.78	269.60	2797.07	668.07	1668.29	398.46	4.0102	0.000018
47	260.08	0.042	23.763	1135.33	271.17	2796.40	667.91	1661.06	396.74	4.0492	0.000018
48	261.38	0.041	24.294	1141.80	272.71	2795.69	667.74	1653.89	395.03	4.0884	0.000018
49	262.66	0.040	24.827	1148.19	274.24	2794.96	667.57	1646.77	393.32	4.1279	0.000018
50	263.92	0.039	25.362	1154.50	275.75	2794.20	667.38	1639.70	391.64	4.1676	0.000018
51	265.16	0.039	25.898	1160.73	277.23	2793.41	667.19	1632.68	389.96	4.2076	0.000018
Давление насыщенного пара (абсолютное)	Температура кипения (конденсации).	Удельный объем = объемная масса (обратная плотность)	Плотность. (пара)	Удельная энтальпия жидкой воды		Удельная энтальпия пара		Удельная теплота парообразования (конденсации)		Теплоемкость пара	Динамическая вязкость пара
бар	°C	м3/кг	кг/м3	кДж/кг	кКал/кг	кДж/кг	кКал/кг	кДж/кг	кКал/кг	кДж/(кг*°C)	кг/(м*с)
52	266.38	0.038	26.437	1166.88	278.70	2792.58	667.00	1625.70	388.29	4.2479	0.000018
53	267.58	0.037	26.978	1172.97	280.16	2791.74	666.79	1618.77	386.64	4.2885	0.000018
54	268.77	0.036	27.521	1178.98	281.59	2790.86	666.59	1611.88	384.99	4.3294	0.000018
55	269.94	0.036	28.067	1184.93	283.02	2789.95	666.37	1605.03	383.35	4.3706	0.000018
56	271.09	0.035	28.614	1190.81	284.42	2789.02	666.15	1598.21	381.73	4.4122	0.000018
57	272.23	0.034	29.164	1196.64	285.81	2788.07	665.92	1591.43	380.11	4.4541	0.000018
58	273.36	0.034	29.716	1202.40	287.19	2787.09	665.68	1584.69	378.50	4.4963	0.000019
59	274.47	0.033	30.270	1208.10	288.55	2786.08	665.44	1577.98	376.89	4.5389	0.000019
60	275.56	0.032	30.827	1213.75	289.90	2785.05	665.20	1571.31	375.30	4.5819	0.000019
61	276.64	0.032	31.386	1219.34	291.23	2784.00	664.95	1564.66	373.71	4.6253	0.000019
62	277.71	0.031	31.947	1224.88	292.56	2782.92	664.69	1558.04	372.13	4.6691	0.000019
63	278.76	0.031	32.511	1230.37	293.87	2781.82	664.43	1551.45	370.56	4.7133	0.000019
64	279.80	0.030	33.077	1235.81	295.17	2780.70	664.16	1544.89	368.99	4.7578	0.000019
65	280.83	0.030	33.646	1241.20	296.45	2779.55	663.89	1538.36	367.43	4.8029	0.000019
66	281.85	0.029	34.218	1246.54	297.73	2778.39	663.61	1531.85	365.88	4.8483	0.000019
67	282.85	0.029	34.792	1251.84	299.00	2777.20	663.32	1525.36	364.33	4.8943	0.000019
68	283.85	0.028	35.368	1257.09	300.25	2775.99	663.03	1518.90	362.78	4.9407	0.000019
69	284.83	0.028	35.948	1262.31	301.50	2774.76	662.74	1512.45	361.24	4.9875	0.000019
70	285.80	0.027	36.529	1267.48	302.73	2773.51	662.44	1506.03	359.71	5.0348	0.000019
71	286.76	0.027	37.114	1272.61	303.96	2772.24	662.14	1499.63	358.18	5.0827	0.000019
72	287.71	0.027	37.702	1277.70	305.17	2770.95	661.83	1493.25	356.66	5.1310	0.000019
73	288.65	0.026	38.292	1282.75	306.38	2769.64	661.52	1486.89	355.14	5.1798	0.000019
74	289.59	0.026	38.885	1287.77	307.58	2768.31	661.20	1480.54	353.62	5.2292	0.000019
Давление насыщенного пара (абсолютное)	Температура кипения (конденсации).	Удельный объем = объемная масса (обратная плотность)	Плотность. (пара)	Удельная энтальпия жидкой воды		Удельная энтальпия пара		Удельная теплота парообразования (конденсации)		Теплоемкость пара	Динамическая вязкость пара
бар	°C	м3/кг	кг/м3	кДж/кг	кКал/кг	кДж/кг	кКал/кг	кДж/кг	кКал/кг	кДж/(кг*°C)	кг/(м*с)
75	290.51	0.025	39.481	1292.75	308.77	2766.97	660.88	1474.21	352.11	5.2791	0.000019
76	291.42	0.025	40.080	1297.70	309.95	2765.60	660.55	1467.90	350.60	5.3295	0.000019
77	292.32	0.025	40.681	1302.61	311.12	2764.22	660.22	1461.61	349.10	5.3805	0.000019
78	293.22	0.024	41.286	1307.49	312.29	2762.81	659.89	1455.32	347.60	5.4321	0.000019
79	294.10	0.024	41.894	1312.34	313.45	2761.39	659.55	1449.06	346.10	5.4843	0.000019
80	294.98	0.024	42.505	1317.15	314.60	2759.95	659.20	1442.80	344.61	5.5370	0.000019
81	295.85	0.023	43.118	1321.94	315.74	2758.50	658.86	1436.56	343.12	5.5904	0.000020
82	296.71	0.023	43.735	1326.70	316.88	2757.03	658.50	1430.33	341.63	5.6443	0.000020
83	297.56	0.023	44.356	1331.42	318.01	2755.54	658.15	1424.11	340.14	5.6989	0.000020
84	298.40	0.022	44.979	1336.12	319.13	2754.03	657.79	1417.91	338.66	5.7542	0.000020
85	299.24	0.022	45.606	1340.79	320.24	2752.50	657.42	1411.71	337.18	5.8101	0.000020
86	300.07	0.022	46.235	1345.44	321.35	2750.97	657.06	1405.52	335.70	5.8666	0.000020
87	300.89	0.021	46.869	1350.06	322.46	2749.41	656.68	1399.35	334.23	5.9239	0.000020
88	301.71	0.021	47.505	1354.66	323.55	2747.84	656.31	1393.18	332.76	5.9818	0.000020
89	302.51	0.021	48.146	1359.22	324.65	2746.25	655.93	1387.02	331.28	6.0404	0.000020
90	303.31	0.020	48.789	1363.77	325.73	2744.64	655.55	1380.87	329.82	6.0998	0.000020
91	304.11	0.020	49.436	1368.29	326.81	2743.02	655.16	1374.73	328.35	6.1599	0.000020
92	304.89	0.020	50.087	1372.80	327.89	2741.39	654.77	1368.59	326.88	6.2208	0.000020
93	305.67	0.020	50.741	1377.27	328.96	2739.73	654.37	1362.46	325.42	6.2825	0.000020
94	306.45	0.019	51.399	1381.73	330.02	2738.07	653.98	1356.34	323.96	6.3450	0.000020
95	307.22	0.019	52.061	1386.17	331.08	2736.38	653.57	1350.22	322.49	6.4083	0.000020
96	307.98	0.019	52.726	1390.58	332.13	2734.69	653.17	1344.11	321.03	6.4725	0.000020
97	308.73	0.019	53.396	1394.98	333.18	2732.98	652.76	1338.00	319.57	6.5376	0.000020
98	309.48	0.018	54.069	1399.35	334.23	2731.24	652.35	1331.89	318.12	6.6036	0.000020
99	310.22	0.018	54.746	1403.71	335.27	2729.50	651.93	1325.79	316.66	6.6705	0.000020
100	310.96	0.018	55.427	1408.05	336.31	2727.74	651.51	1319.69	315.20	6.7385	0.000020

Энтальпия для начинающих (I-d диагр). Расчет количества конденсата. Скрытая холодопроизводительность

Энтальпия. Этому элементу I-d диаграммы я посвятил отдельную тему, потому как для меня этот элемент являлся наименее понятным среди остальных (температуры, влагосодержания и относительной влажности) и требующим разбора других попутных понятий.Продублирую рисунок из прошлой статьи http://mrcynognathus.livejournal.com/7641.html:

Не буду глубоко вдаваться в терминологию, скажу лишь, что я понимаю энтальпию воздуха, как энергию, которую хранит в себе определенный объем воздуха. Эта энергия является потенциальной, то есть в условии равновесия воздух не тратит эту энергию и не поглощает её из других источников.

Не буду даже приводить пример для разъяснения своего определения (хотя хотел), потому как, по моему мнению, это запутает и уведет в сторону.

Сразу к делу – что главное мы можем взять из энтальпии? – отвечаю – энергию (или количество теплоты), которую нужно передать воздуху, чтобы нагреть его или отнять, чтобы его охладить (или осушить).

Например, у нас есть задача - посчитать какой мощности нам нужен калорифер, чтобы осенью или весной подать в помещение 1200 м3/ч нагретого до температуры плюс 20 градусов наружного воздуха. Расчетная температура наружного воздуха в переходный период – плюс 10 градусов при энтальпии 26,5 кДж/кг (по СП 60.13330.2012).

Задача решается легко. Для того чтобы решить такую простую задачку используя и-д диаграмму, нам необходимо ввести в уровень понимания единицы измерения некоторых физических величин:1) Энтальпия – килоДжоуль/килограмм . То есть количество потенциальной энергии в одном килограмме воздуха. Здесь все просто – если энтальпия равна 20, то это означает, что в одном килограмме данного воздуха находится 20 килоджоулей потенциальной теплоты или 20000 джоулей.2) Мощность калорифера – Ватты, но в то же время ватты можно разложить на Джоуль/секунда. То есть, сколько может выдать калорифер энергии за одну секунду. Чем больше энергии нам сможет выдать калорифер за секунду, тем он мощнее. И тут все просто.

Итак, берем I-d диаграмму и ставим на ней точку наружного воздуха. После, проводим прямую линию вверх (идет нагрев воздуха без изменения влагосодержания).

Мы получаем точку на j-d диаграмме с температурой плюс 20 градусов и энтальпией 36,5 кДж/кг. Возникает вопрос – что, же, черт возьми, нам дальше делать с этой гребанной информацией?! :)

Во первых, обратим внимание на то, что мы производили все операции с одним килограммом воздуха (это косвенно видно по единице измерения энтальпии кДж/кг).

Во вторых, у нас был килограмм воздуха с 26,5 кДж, а стал с 36,5 кДж потенциальной энергии. То есть килограмму воздуха сообщили 10 кДж для того чтобы его температура поднялась с плюс 10 градусов до плюс двадцати.

Дальше мы переведем 1200 м3/ч в кг/с(килограммы/секунда, т.к. на I-d диаграмме используются эти единицы измерения), умножив 1200 на 1,25 кг/м3 (один метр кубический десятиградусного воздуха весит 1,25 килограмма), что даст нам 1500 кг/ч, а затем разделив на 3600 (обратите внимание на логику перевода между системами – делим мы на 3600 не потому что мы так зазубрили или запомнили, а потому что за секунду у нас воздуха пройдет меньше чем за час, меньше в 3600 раз) получаем итог 0,417 кг/с.

Идем дальше. Мы получили, что за одну секунду проходит 0,417 кг воздуха. И мы знаем, что каждому килограмму необходимо передать (сообщить) 10 кДж для того, чтобы нагреть его до температуры плюс 20 градусов. Сообщаем, умножая 0,417 кг/с на 10 кДж/кг, и получая 4,17 кДж/с (килограммы сократились) или 4170 Дж/с, что равно 4170 Вт (определено нами ранее по тексту). Вот мы и получили мощность нашего калорифера.

Кондиционирование

Охлаждение происходит по тому же принципу, но только немного сложнее из-за выделения влаги из воздуха.

Выделение влаги (конденсата) из воздуха происходит тогда, когда температура воздуха при охлаждении достигает точки росы на линии относительной влажности 100%. В предыдущей статье я описал этот процесс: http://mrcynognathus.livejournal.com/7641.html

Вроде бы, нет ничего сложного - охлаждаем воздух с температурой плюс 20 градусов и относительной влажностью 50% до плюс 12 градусов (как это обычно происходит в сплит-системах), проводя прямую вертикально вниз из точки 20-ти градусного воздуха до точки 12-ти градусного воздуха.

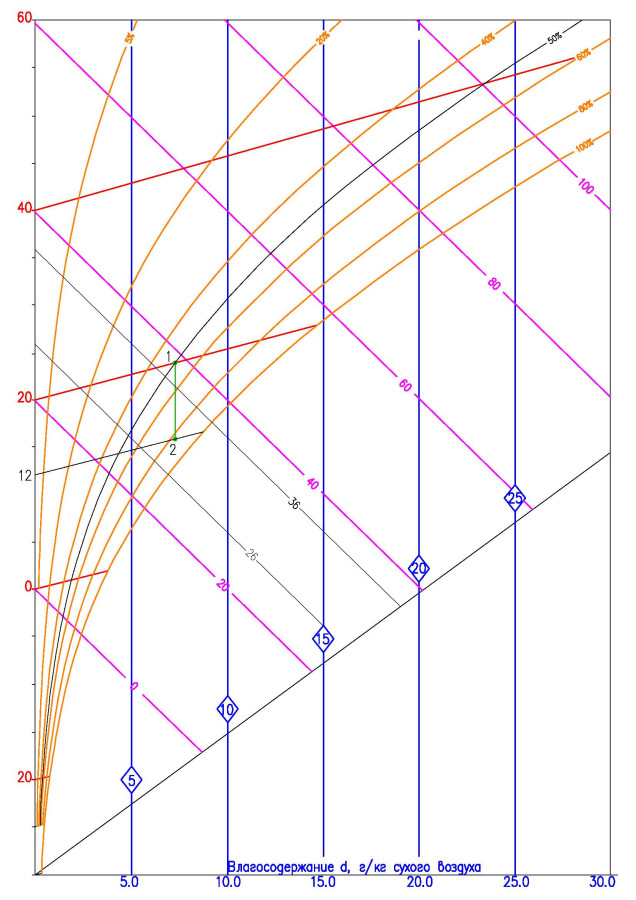И что мы видим – никаких влаговыделений. Влагосодержание осталось на прежнем уровне – 8 г/кг. Но мы то знаем, что при работе кондиционера идет обильное влаговыделение (конденсат активно капает из дренажной трубки, выведенной на фасад здания) – этот факт подтверждается неоднократным наблюдением гуляющего по летним улицам.

Возникает вопрос – откуда же влага? Ответ: дело в том, что через внутренний блок кондиционера проходят медные трубки, которые охлаждаются хладагентом до температур, которые ниже плюс 12 градусов, и в связи с этим охлаждаемый воздух делится на слои с различной температурой, примерно как на рисунке ниже (предположим, что трубки охлаждаются до плюс 5 градусов). Сразу скажу, что это далекий от действительности, но показывающий общий смысл вышесказанных мною слов рисунок (прошу меня за него не ругать)

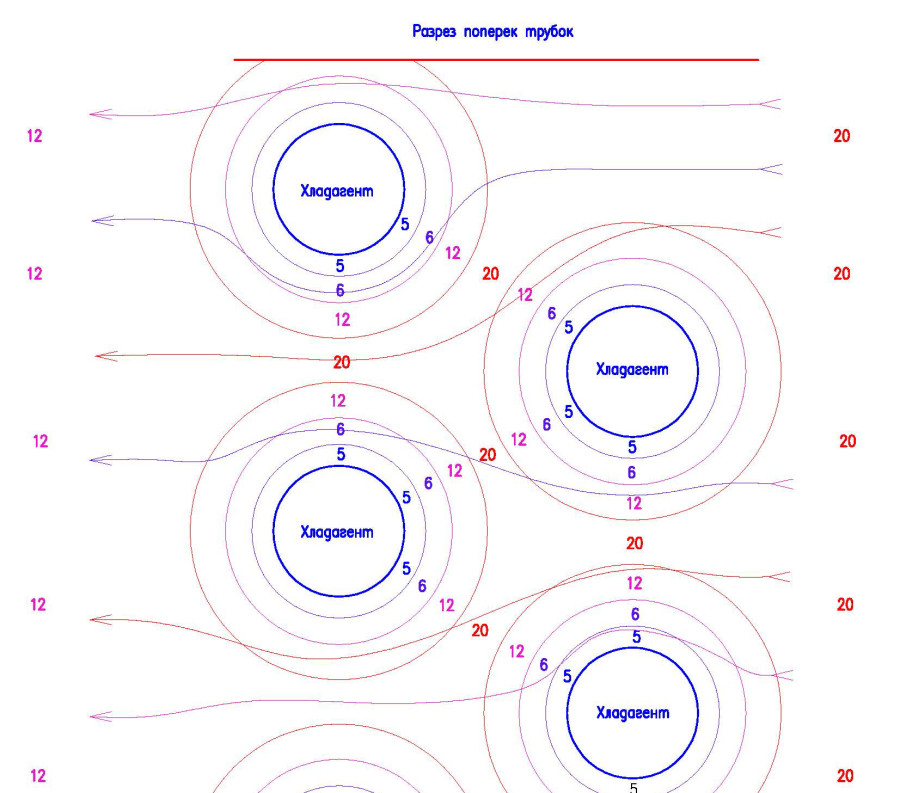Поэтому из того воздуха, который соприкасается с трубками(и оребрением) и выпадает влага. А тот воздух, что не успел охладиться до точки росы, или успел, но избежал контакта с охлажденной поверхностью, минует процесс влаговыделения и несет в себе столько же влаги, сколько он нес в себе до охлаждения (по сути).

Для того чтобы провести правильную прямую процесса охлаждения воздуха в таком охладителе (где температура хладагента ниже температуры точки росы), нам необходимо учесть каждый воздушный поток с различными тепловлажностными параметрами воздуха и найти на графике точки смешения всех этих потоков – что по моему мнению – не реально (у меня просто не хватит мозгов на это)! Но…

...Я пришел к вот такому решению (скорее всего не я такой один) - у нас есть температура входящего воздуха, есть температура хладагента и есть температура получаемого воздуха, и я считаю, что нам достаточно провести линию процесса охлаждения части воздуха до плюс 5 градусов и найти точку смешения 5-ти градусного воздуха и 20-ти градусного воздуха. То есть, я предполагаю, что проходя через внутренний блок кондиционера, воздух делится на два потока – тот, который охлаждается до плюс пяти градусов и выдает нам наибольшее количество влаги, и тот который вообще не охлаждается, а на выходе эти два потока смешиваются и образуют поток воздуха с температурой плюс 12 градусов и определенным влагосодержанием.

Я считаю, что для достижения тех целей, которые я преследую, результата, полученного при таком упрощении, вполне достаточно. А какие же цели я преследую?

Первая цель – это определение максимального влаговыделения для того, чтобы рассчитать систему конденсатоотвода (особенно актуально это при системах кондиционирования, в составе которых две и более охлаждающих установок)

Вторая цель – учесть количество холода, идущего на перевод воды из газообразного состояния в жидкое (на конденсацию влаги; так назывемая скрытая холодопроизводительность). Особенно актуально это при охлаждении (отведении тепла) во влажных помещениях. Например, нам необходимо отвести от определенного насоса 2 кВт тепла, которые он выделяет в помещение. Если мы не учтем, что помещение влажное (влажное, по каким либо причинам) и установим в помещение сплит-систему мощностью 2,5 кВт, то мы можем получить (при определенных условиях), что сплит-система тратит 1 кВт лишь для того, чтобы перевести пар во влагу, а на удаление теплоизбытков тратит оставшиеся 1,5 кВт, что меньше на 500 Вт необходимого, и что может привести к перегреву насоса и скорого его выхода из строя.

Итак, делим поток на два потока, один из которых охлаждаем до плюс пяти - отрезок 1-2, а другой оставляем не тронутым - точка 1.

Смешиваем эти два потока, объединяя получившиеся точки прямой 1-3-2, и находим нашу 12-ти градусную точку на получившейся прямой.

Оставляем прямую 1-3 как линию процесса охлаждения воздуха в сухом охладителе с температуры плюс 20 градусов до плюс 12 градусов с выделением конденсата.

Для того чтобы узнать количество конденсата, выпавшего на оребрении и трубках охладителя нам необходимо вычесть влагосодержание получившегося воздуха из влагосодержания необработанного воздуха 7,3 г/кг – 6,3 г/кг. В итоге мы получим, что из каждого килограмма прошедшего через охладитель воздуха выделится 1 грамм конденсата. Чтобы узнать расход конденсата, нам необходимо узнать, сколько килограммов воздуха проходит через теплообменник за определенное время. Например, если нам необходимо охладить 1400 м3/ч воздуха с температуры плюс 20 градусов с относительной влажностью 50% до температуры плюс 12 градусов, то мы переведем 1400 м3/ч в 1680 кг/ч и получим, что за час обработки воздуха выделится 1680 грамм конденсата (по одному грамму на каждый килограмм воздуха), что равно 0,47 г/с (грамм/секунда) и 0,47 * 10-3 кг/с.

Полная холодопроизводительность находится так же, как мы искали теплопроизводительность калорифера ранее. Берем энтальпию начальной точки 28 кДж/кг, вычитаем из нее энтальпию конечной точки 38,5 кДж/кг, получая отрицательное число 10,5 кДж/кг (минус указывает на то, что энергия отдается хладагенту). Переводим 1680 кг/ч в килограмм/секунда, что будет равняться 0,47 кг/с. В итоге получаем 4,935 кДж/с, что равно 4,935 кВт мощности.

Подпишись на мой YouTube-канал FAN-tastiK - канал о проектировании Вентиляции, Кондиционирования и Отопления

Если есть необходимость определить скрытую холодопроизводительность , можно найти её, отталкиваясь от количества выделенного конденсата, используя удельную теплоту парообразования:Теплота, требуемая для конденсации влаги, находится по формуле: Q = L * m,где L – удельная теплота парообразования; m – масса влаги.L воды равно: 2260 кДж/кг.

Для того, чтобы перевести 0,47 грамма воды из газообразного состояния в жидкое состояние за секунду нам требуется 2260 Дж * 103 * 0,47 кг/с * 10-3 = 1063 Дж/с, что равно 1063 Вт.

Итак скрытая холодопроизводительность данного процесса равна 1063 Вт.

Это Все

Собственно, это все, что я хотел рассмотреть в данной статье. Прошу не бранить меня за наивную упрощенность описанного мною - я постарался объяснить в первую очередь себе - что такое энтальпия и как ей пользоваться. Надеюсь Вам было интересно и полезно. Спасибо за внимание.

P.S. Эта статья не в коем случае не является учебным пособием. Она лишь мое субъективное видение вопроса. Я бы даже сказал - каждое слово, написанное в этой статье, является ошибочным. Информацию, достойную носить звание "Научная истина" ищите в учебниках.

P.P.S Предыдущая статья, в которой я описывал собственное видение таких элементов I-d диаграммы (диаграммы Рамзина) как температура, влагосодержание, относительная влажность находится здесь: http://mrcynognathus.livejournal.com/7641.html

mrcynognathus.livejournal.com

ЭНТАЛЬПИЯ ОБРАЗОВАНИЯ ВОДЫ, Тепловой эффект химической реакции

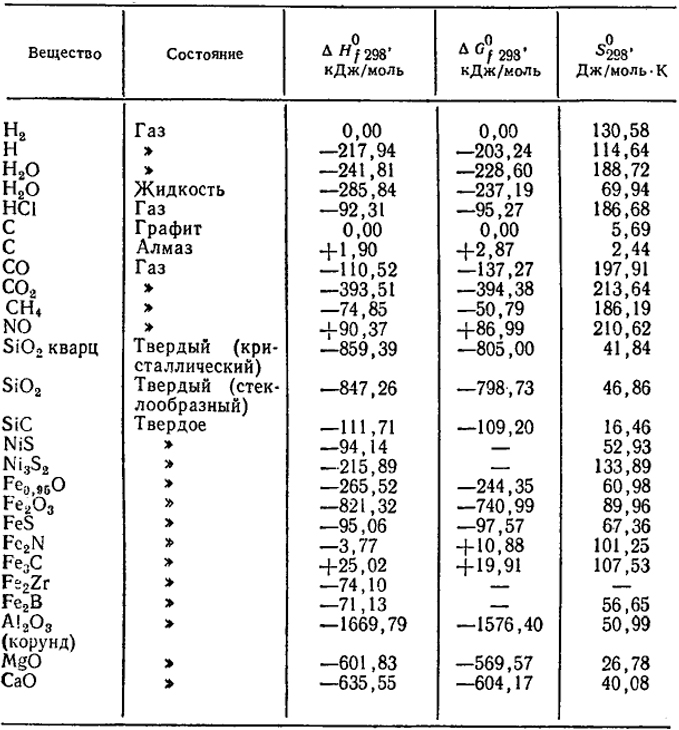Стандартная энтальпия сгорания — ΔHгоро, тепловой эффект реакции сгорания одного моля вещества в кислороде до образования оксидов в высшей степени окисления. Стандартные энтальпии образования веществ при температуре 298 К приведены в справочниках. Энтальпия образования позволяет рассчитать ∆H через вычисление реакций образования реагентов и продуктов. Энтальпии образования простых веществ при стандартных условиях являются их основными энергетическими характеристиками.

Проще говоря, энтальпия — это та энергия, которая доступна для преобразования в теплоту при определенном постоянном давлении. Энтальпия системы H — аналогично внутренней энергии и другим термодинамическим потенциалам — имеет вполне определенное значение для каждого состояния, то есть является функцией состояния.

Так, энтальпия образования — количество энергии, которое выделяется или поглощается при образовании сложного вещества из простых веществ. В случае эндотермических реакций система поглощает тепло и ΔН — величина положительная. Энтальпия — величина аддитивная (экстенсивная), то есть для сложной системы равна сумме энтальпий её независимых частей H=∑Hi{\displaystyle H=\sum H_{i}}.

Метод 2 из 3: Подсчет энтальпии

Стандартным также может быть принято, например, состояние вещества в предельно разбавленном растворе. Диск Плимсоля» в таком случае означает собственно стандартное состояние вещества, независимо от его выбора. Термохимические эффекты можно включать в химические реакции. Реакции, сопровождающиеся выделением тепла в окружающую среду имеют отрицательный тепловой эффект и называются экзотермическими.

Чтобы рассчитать температурную зависимость энтальпии реакции, необходимо знать мольные теплоемкости веществ, участвующих в реакции. Стандартная энтальпия растворения — ΔHраство, тепловой эффект процесса растворения 1 моля вещества в бесконечно большом количестве растворителя. Во многих случаях эти реакции протекают при постоянном объеме или постоянном давлении.

Для того, чтобы облегчить сравнение энтальпий различных реакций, используют понятие «стандартного состояния». Стандартное состояние — это состояние чистого вещества при давлении 1 бар (= 105 Па) и заданной температуре. В термохимических уравнениях указывают не только формулы веществ, но и их агрегатные состояния или кристаллические модификации.

Согласно этому определению, энтальпия образования наиболее устойчивых простых веществ в стандартном состоянии равна 0 при любой температуре. Понятия «энтальпия образования» используют не только для обычных веществ, но и для ионов в растворе. Следствие 3. Энтальпия химической реакции равна разности энергий разрываемых и образующихся химических связей.

Cp — разность изобарных теплоемкостей продуктов реакции и исходных веществ. Рассчитайте энтальпию испарения воды при этой температуре. H0исп = -241.8 — (-285.8) = 44.0 кДж/моль. В данной реакции химические связи не разрываются, а только образуются. 3-2. Стандартная энтальпия реакции CaCO3(тв) = CaO(тв) + CO2(г), протекающей в открытом сосуде при температуре 1000 К, равна 169 кДж/моль.

Рассчитайте теплоту образования оксида натрия fH0298(Na2O), если fH0298(h3Oж) = -285.8 кДж/моль. Какова энтальпия атомизации аммиака, если энтальпия образования аммиака равна -46.2 кДж/моль? 3-17. Энтальпия диссоциации карбоната кальция при 900 оС и давлении 1 атм равна 178 кДж/моль. Количество воды на поверхности Земли оценивается в 1 390 000 000 000 000 000 т, большая часть из которых находится в морях и океанах. 1 моль N2O5 в этой реакции из внешней среды в систему передается теплота, равная 11 кДж: ΔH°(N2O5) = +22 кДж ÷ 2 моль = +11 кДж/моль.

Природные и антропогенные источники:

Во всех расчетах обязательно необходимо принимать во внимание и указывать энтальпии образования всех веществ и простых и сложных. Рассчитывается энтальпия так: ∆H = m x s x ∆T, где m – это масса реагентов, s – это теплоемкость, ∆T – это разница температуры.

Продукт реакции создается в результате взаимодействия реагентов. Например, необходимо найти энтальпию реакции образования воды из водорода и кислорода: 2h3 (Водород) + O2 (Кислород) → 2h3O (Вода). Далее определите теплоемкость продукта реакции. Обратите внимание на то, что при наличии нескольких продуктов реакции, вам потребуется рассчитать теплоемкость каждого, а затем сложить их, чтоб получить энтальпию всей реакции.

Кристаллические модификации, цвет растворов и паров:

Теперь мы найдем ∆T – изменение температуры до и после реакции. Найдите энтальпию по формуле ∆H = m x s x ∆T. Если известна m – масса реагентов, s – теплоемкость продукта реакции и ∆T – изменение температуры, то можно подсчитать энтальпию реакции.

При вычислении энтальпии образования, формулу для определения энтальпии реакции продукта вы переворачиваете, то знак энтальпии должен поменяться. Изменение энтальпии (или Тепловой эффект химической реакции) не зависит от пути процесса, определяясь только начальным и конечным состоянием системы.

mariantas.ru

Энтальпия воды и водяного пара

В таблицах сухого насыщенного пара (по давлениям) в первом вертикальном столбце приводятся значения давлений, а по горизонтальным строчкам против каждого значения давления даются соответствующие этому давлению значения температуры, удельных объемов, плотностей, теплосодержаний (энтальпии) воды и водяного пара, теплоты парообразования и др. [c.18] По таблицам [Вук] энтальпии воды и водяного пара при / = =200 и Р = 15,857 кг/см соответственно равны 667,0 й 203,5 ккал/кг. Определить критическое давление. Результат сравнить с табличной величиной. [c.171]

Международные скелетные таблицы удельных объемов и энтальпии воды и водяного пара при давлениях до 1000 бар и температурах до 800° С, включая и данные на линии насыщения, были утверждены VI Международной конференцией (Нью-Йорк, 1963 г.) [2]. Международные скелетные таблицы коэффициента динамической вязкости при давлениях до 800 бар и температурах до 700° С и коэффициента теплопроводности при давлениях до 500 бар и температурах до 700° С после дополнительного анализа специально выделенной рабочей группой были утверждены делегациями указанной конференции в 1964 г. [3]. [c.7]

Эта температура близка к предварительно принятой выше. Если бы она значительно отличалась, расчет следовало бы повторить с использованием других значений энтальпий воды и водяных паров, а также тепловых эффектов образования кислоты. [c.43]

По таблицам [Вук] энтальпии воды и водяного пара при =200 и Р = 15,857 кг ся соответственно равны 667,0 н [c.177]

В приведенных выше примерах ( 2—7) использование данных по теплоемкостям имеет не только научное, но нередко и большое прикладное значение. Кроме того, в промышленности часто возникают специфические вопросы, которые не охватываются рассмотренными случаями. Так, знание теплоемкостей чистых веществ и их смесей необходимо для расчета тепловых балансов реакторов, печных установок и т. д., что имеет большое значение при проектировании и строительстве предприятий химической и металлургической промышленности, в производстве строительных материалов и многих других областях народного хозяйства. Для технического усовершенствования и повышения экономичности паровых двигателей нужно знать с большой точностью теплоемкость и энтальпию воды и водяного пара до весьма высоких значений температуры и давления. Эти и многие другие потребности не всегда могут быть удовлетворены имеющимися в литературе данными и нуждаются в постановке специальных работ по экспериментальному определению теплоемкостей и теплот фазовых переходов. [c.256]

ДОЛЛ примеси (до 3% водяного пара в воздухе и до 5% азота в природном газе по весу) и большой по абсолютной величине энтальпией воды и водяного пара. [c.39]

Энтальпийные диаграммы растворов широко применяют в неорганической технологии при расчетах материальных и тепловых балансов процессов растворения, кристаллизации, упаривания, разбавления и других, особенно при повышенных температурах и давлениях. Общий вид энтальпийной диаграммы (а) и диаграммы растворимости (б) для двухкомпонентной системы с насыщением только безводным соединением представлены на рис. 4.5. Ось абсцисс — ось составов растворов в пересчете на безводное вещество А. На левой ординате верхней части рисунка (с = 0) отложены значения удельной энтальпии воды и водяного пара в широком диапазоне температур. На правой ординате, исходящей из точки Сд = 100 %, — энтальпийная характеристика безводных твердых фаз. [c.84]

В модулях библиотеки ФИЗХИМ рассчитываются следующие основные свойства газовых смесей энтальпия, теплоемкость, плотность, энтропия, вязкость, теплопроводность, коэффициенты диффузии, а также константы равновесия произвольных химических реакций (для 56 веществ, входящих в банк), энтальпии воды и водяного пара, давление насыщенного водяного пара (от температуры) и температуры его (от давления), молекулярная масса газовых смесей. Кроме модулей вычисления свойств имеется полезный модуль определения температуры газовой смеси по заданной ее энтальпии (и, естественно, составу). Он щироко используется в расчетах тепловых балансов. [c.429]

chem21.info