Содержание
Архимедова сила — закон, формула, определение
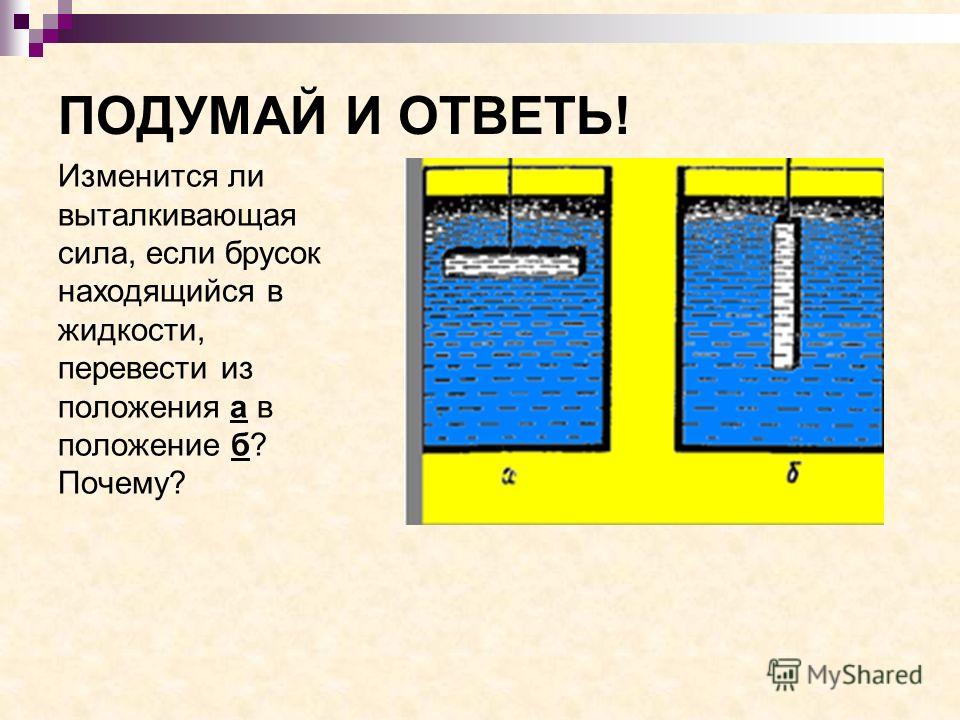
Легенду об открытии закона Архимеда многие знают с детства. Но на уроках физики в 7 классе этой историей не отделаешься: надо еще знать, как действует архимедова сила, в чем измеряется и как ее вычислить.
Сила: что это за величина
Прежде чем говорить о силе Архимеда, нужно понять, что это вообще такое — сила.
В повседневной жизни мы часто видим, как физические тела деформируются (меняют форму или размер), ускоряются и тормозят, падают. В общем, чего только с ними не происходит! Причина любых действий или взаимодействий тел — ее величество сила.
Сила — это физическая векторная величина, которая воздействует на данное тело со стороны других тел. Сила измеряется в ньютонах — единице измерения, которую назвали в честь Исаака Ньютона.
Поскольку сила — величина векторная, у нее, помимо модуля, есть направление. От того, куда направлена сила, зависит результат.
От того, куда направлена сила, зависит результат.
Вот стоите вы на лонгборде: можете оттолкнуться вправо, а можете влево — в зависимости от того, в какую сторону оттолкнетесь, результат будет разный. В этом случае результат выражается в направлении движения.
Практикующий детский психолог Екатерина Мурашова
Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков
Открытие закона Архимеда
Так вышло, что закон Архимеда известен не столько своей формулировкой, сколько историей возникновения.
Легенда гласит, что царь Герон II попросил Архимеда определить, из чистого ли золота сделана его корона, при этом не причиняя вреда самой короне. То есть расплавить корону или растворить — нельзя.
Взвесить корону Архимеду труда не составило, но этого было мало — нужно ведь определить объем короны, чтобы рассчитать плотность металла, из которого она отлита.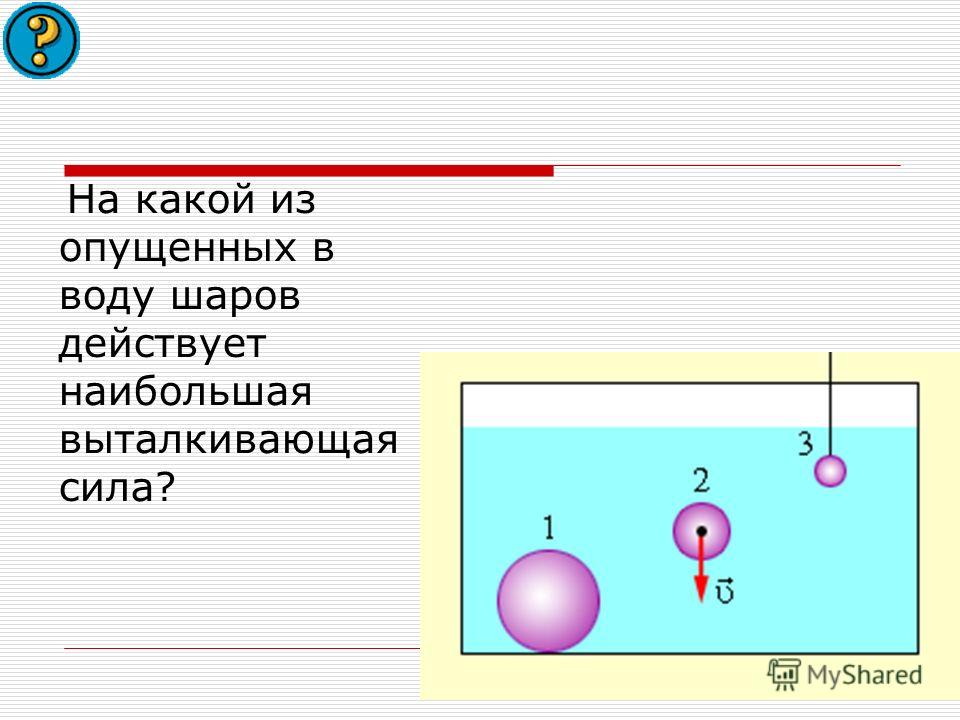
Рассчитать плотность металла, чтобы установить, золотая ли корона, можно по формуле плотности.
Формула плотности тела ρ = m/V ρ — плотность тела [кг/м3] m — масса тела [кг] V — объем тела [м3] |
Дальше, согласно легенде, Архимед, озабоченный мыслями о том, как определить объем короны, погрузился в ванну — и вдруг заметил, что уровень воды в ванне поднялся. Тут ученый осознал, что объем его тела вытеснил равный ему объем воды, следовательно, и корона, если ее опустить в заполненный до краев таз, вытеснит из него объем воды, равный ее объему.
Решение задачи было найдено и, согласно самой расхожей версии легенды, ученый закричал «Эврика!» и побежал докладывать о своей победе в царский дворец (и так торопился, что даже не оделся). 🤦🏻♂️
Попробуйте онлайн-курс подготовки к ЕГЭ по физике с опытным преподавателем в Skysmart!
Формула и определение силы Архимеда для жидкости
На поверхность твердого тела, погруженного в жидкость, действуют силы давления. Эти силы увеличиваются с глубиной погружения, и на нижнюю часть тела будет действовать со стороны жидкости большая сила, чем на верхнюю.
Равнодействующая всех сил давления, действующих на поверхность тела со стороны жидкости, называется выталкивающей силой или силой Архимеда. Истинная причина появления выталкивающей силы — наличие различного гидростатического давления в разных точках жидкости.
Определение архимедовой силы для жидкостей звучит так:
Выталкивающая сила, действующая на тело, погруженное в жидкость, равна по модулю весу вытесненной жидкости и противоположно ему направлена.
Формула архимедовой силы для жидкости FАрх = ρжgVпогр ρж — плотность жидкости[кг/м3] Vпогр — объем погруженной части тела [м3] g — ускорение свободного падения [м/с2] На планете Земля g = 9,8 м/с 2. |
А теперь давайте порешаем задачки, чтобы закрепить, как вычислить архимедову силу.
Задача 1
В сосуд погружены три железных шарика равных объемов. Одинаковы ли силы, выталкивающие шарики? Плотность жидкости вследствие ничтожно малой сжимаемости на любой глубине считать примерно одинаковой.
Решение
Да, так как объемы одинаковы, а архимедова сила зависит от объема погруженной части тела, а не от глубины.
Задача 2
На графике показана зависимость модуля силы Архимеда FАрх, действующей на медленно погружаемый в жидкость кубик, от глубины погружения x. Длина ребра кубика равна 10 см, его нижнее основание все время параллельно поверхности жидкости. Определите плотность жидкости. Ускорение свободного падения принять равным 10 м/с2.
Решение
Сила Архимеда, действующая на кубик, равна FАрх = ρжgVпогр.
Vпогр. — объем погруженной части кубика,
ρж — плотность жидкости.
Учитывая, что нижнее основание кубика все время параллельно поверхности жидкости, можем записать:
FАрх = ρжgV погр = ρжga 2x
где а — длина стороны кубика.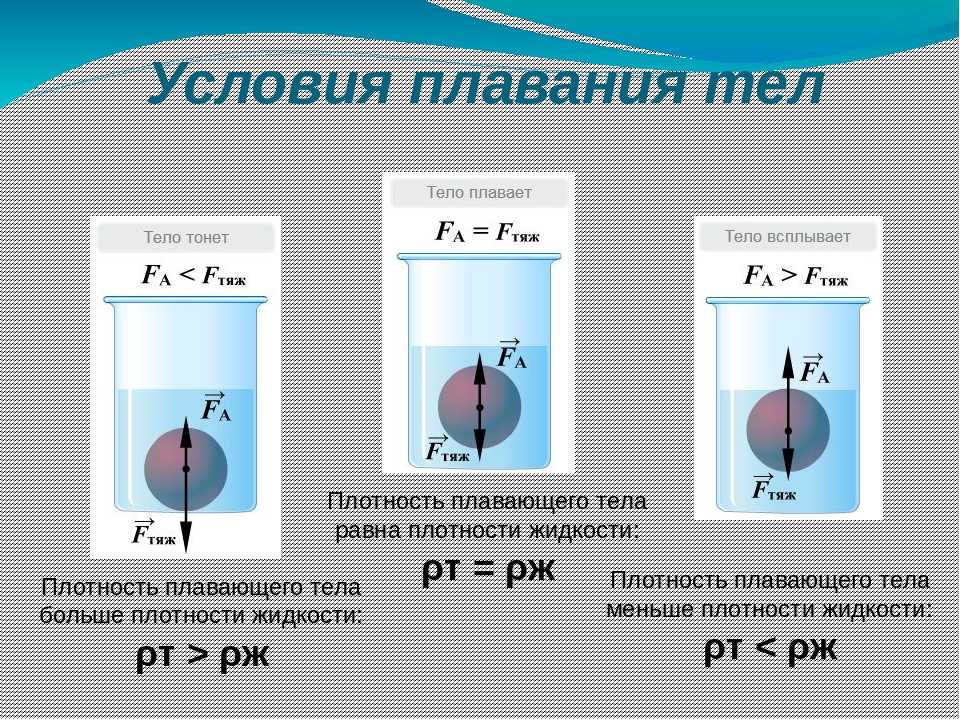
Выразим плотность:
ρ = FАрх / ga2x
Рассматривая любую точку данного графика, получим:
ρ = FАрхga2x = 20,25 / 10 × 7,5 × 10-2 = 2700 кг/м3
Ответ: плотность жидкости равна 2700 кг/м 3.
Условия плавания тел
Из закона Архимеда вытекают следствия об условиях плавания тел.
Погружение | Плавание внутри жидкости | Плавание на поверхности жидкости |
ρж < Если плотность тела больше, чем плотность жидкости или газа, — оно уйдет на дно. | ρж = ρт Если плотности тела и жидкости или газа равны — тело будет находиться в безразличном равновесии в толще жидкости или газа. | ρж > ρт Если плотность тела меньше плотности жидкости или газа — оно будет плавать на поверхности. |
Почему корабли не тонут?Корабль сделан из металла, плотность которого больше плотности воды. И, по идее, он должен тонуть. Но дело в том, что корпус корабля заполнен воздухом, поэтому общая плотность судна оказывается меньше плотности воды, и сила Архимеда выталкивает его на поверхность. Если корабль получит пробоину, то пространство внутри заполнится водой — следовательно, общая плотность корабля увеличится. В подводных лодках есть специальные резервуары, которые заполняют водой или сжатым воздухом. Если нужно уйти на глубину — водой, если подняться — сжатым воздухом. Рыбы используют такой же принцип в плавательном пузыре — наполняют его воздухом, чтобы подняться наверх. Человеку, чтобы не утонуть, тоже достаточно набрать в легкие воздух и не двигаться — вода будет выталкивать тело на поверхность. Именно поэтому важно не тратить силы и кислород в легких на панику и борьбу, а расслабиться и позволить физическим законам сделать все за нас. |
Формула и определение силы Архимеда для газов
На самом деле тут все очень похоже на жидкости. Начнем с формулировки закона Архимеда:
Выталкивающая сила, действующая на тело, погруженное в газ, равна по модулю весу вытесненного газа и противоположно ему направлена.
Формула архимедовой силы для газов FАрх = ρгgVпогр ρг — плотность газа [кг/м3] Vпогр — объем погруженной части тела [м3] g — ускорение свободного падения [м/с2] На планете Земля g = 9,8 м/с 2. |
Сила Архимеда для газов действует аналогично архимедовой силе для жидкостей. Давайте убедимся в этом, решив задачку.
Задача
Груз какой максимальной массы может удерживать воздушный шар с гелием объема 0,3 м3, находясь в атмосфере Земли? Плотность воздуха равна 1,3 кг/м 3. Гелий считать невесомым.
Гелий считать невесомым.
Решение
Подставляем значения и получаем:
FАрх = ρгgVпогр = 1,3 × 10 × 0,3 = 0,39 Н
По второму закону Ньютона для инерциальных систем отсчета:
FАрх = mg
Выражаем массу груза и подставляем значения:
m = FАрх / g = 0,39 / 10 = 0, 039 кг = 39 кг
Ответ: груз максимальной массы 39 г может удержать данный шарик с гелием.
Когда сила Архимеда не работает
Архимедова сила не работает лишь в трех случаях:
Невесомость. Главное условие возникновения Архимедовой силы — это наличие веса у среды. Если мы находимся в невесомости, холодный воздух не опускается, а горячий, наоборот, не поднимается.

Тело плотно прилегает к поверхности. Отсутствие газа или жидкости между поверхностью и телом свидетельствует об отсутствии выталкивающей силы — телу просто неоткуда выталкиваться.
Растворы и смеси. Если взять спирт, плотность которого меньше плотности воды, и смешать его с водой, получится раствор. На него не будет действовать сила Архимеда, несмотря на то, что плотность спирта меньше плотности воды — он просто растворится.
Выталкивающая сила — вода — Большая Энциклопедия Нефти и Газа, статья, страница 1
Cтраница 1
Выталкивающая сила воды на трубопровод д учитывается как результирующая распределенная нагрузка, интенсивность которой равна разнице веса трубы на поверхности и в воде.
[1]
N — выталкивающая сила воды ( сила реакции воды), направленная вверх.
[2]
При расчете поправки на выталкивающую силу воды Д0 принято, что GB Gr; это допустимо, так как выталкивающая сила мала.
[3]
При расчете поправки на выталкивающую силу воды ДОВ принято, что Ов Ог; это допустимо, так как выталкивающая сила мала.
[4]
Поперечная нагрузка на трубопровод от выталкивающей силы воды зависит от уровня воды относительно трубы.
[5]
Нагрузка на анкеры определяется величиной выталкивающей силы воды, кроме того, она зависит от упругой линии трубопровода при укладке на дно траншеи, внутреннего давления и допустимого температурного перепада, а также от податливости анкеров. Как показали расчеты, при одинаковом шаге анкеров при неизменности свойств грунта, в который они погружены, нагрузки на анкеры, устанавливаемые на участках упругого изгиба, различны. Поэтому для обеспечения надежной работы системы при проектировании трубопровода необходимо расстояние между анкерами определять с учетом всех параметров. Неравномерность нагрузки на анкеры особенно сказывается на участках, где изменяются физико-механические характеристики грунтов. Использование программы Анкер в практике проектирования позволяет с учетом всех факторов назначать расстояние между анкерами.
Неравномерность нагрузки на анкеры особенно сказывается на участках, где изменяются физико-механические характеристики грунтов. Использование программы Анкер в практике проектирования позволяет с учетом всех факторов назначать расстояние между анкерами.
[6]
Поперечная нагрузка на трубопровод от выталкивающей силы воды зависит от уровня воды относительно трубы.
[7]
Учитывая, что в большинстве случаев воздействие выталкивающей силы воды является многократным нагружением, то удерживающую способность грунта, взаимодействующего с трубопроводом и анкерами, следует учитывать только в области упругих деформаций грунта.
[8]
Расчеты устойчивости трубопровода от всплытия только от действия выталкивающей силы воды выполненные по [2], показывают, что грунтовааг засыпка толщиной 0 5 — 0 6 м от верхней образующей трубы не обеспечивает устойчивого положения.
[9]
Расчеты устойчивости трубопровода от всплытии только от действия выталкивающей силы воды выполненные по 2 ], показывают, что грунтовая засыпка толщиной 0 5 — 0 6 м от верхней образующей трубы не обеспечивает устойчивого положения трубопровода.
[10]
При укладке трубопроводов в болотистых и обводненных районах должна учитываться выталкивающая сила воды.
[11]
Вертикальная составляющая Ру действует в том же направлении, что и выталкивающая сила воды дв и, следовательно вводится в основную формулу (4.60) с тем же положительным знаком.
[12]
| Датчик-реле уровня.
[13] |
Принцип работы датчика реле основан на изменении положения поплавка 9 под действием выталкивающей силы воды. Поплавок при перемещении рычагом 7 воздействует на микропереключатель 17, включенный в электрическую цепь сигнализации. Силь-фон 8 выполняет функцию разделителя между водой в баке и окружающей средой.
[14]
Средний участок газопровода, находящийся в воде, в нормальном режиме эксплуатации под действием выталкивающей силы воды может приподниматься вверх.
[15]
Страницы:
1
2
3
4
Выталкивающая сила воды | Научный проект
Научный проект
Почему камень тонет в воде, а гигантский стальной авианосец плавает? Авианосец на намного тяжелее на , но легко скользит по поверхности океана.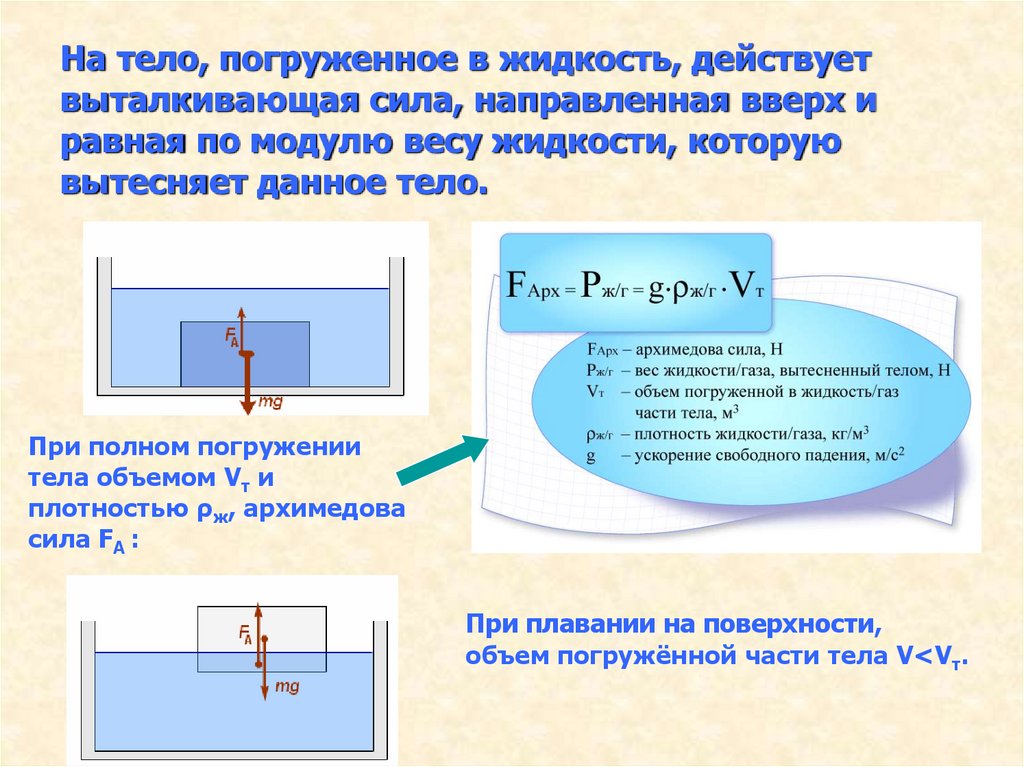 Понятно, что вес — это еще не все. Так что же происходит? Что определяет, плавает что-то или нет? В этом эксперименте вы узнаете, как вода и гравитация работают вместе, чтобы удержать ваш корабль на плаву или утащить его на дно моря.
Понятно, что вес — это еще не все. Так что же происходит? Что определяет, плавает что-то или нет? В этом эксперименте вы узнаете, как вода и гравитация работают вместе, чтобы удержать ваш корабль на плаву или утащить его на дно моря.
Сколько веса вы можете добавить к лодке, прежде чем она утонет?
Скачать проект
Оценка
Шестой класс — Восьмой класс
Предмет
Наука
- Неглубокий пластиковый стаканчик (например, пластиковый контейнер для супа на вынос из ресторана или пустая банка из-под сливочного сыра)
- Ванна или раковина, наполненная водой (достаточно широкая, чтобы «лодка» могла плавать, и достаточно глубокая, чтобы ее можно было полностью погрузить в воду)
- Несколько кварталов
- Измерьте объем вашей «лодки». Самый простой способ сделать это — наполнить его водой, а затем налить воду в мерный стакан.
 Количество воды в лодке говорит о ее объеме.
Количество воды в лодке говорит о ее объеме. - Рассчитайте, сколько граммов воды может вместить лодка (один миллилитр воды равен одному грамму).
- Опусти пустую лодочку в ванну или раковину и начни добавлять четвертак по одной. Добавляйте их медленно, чтобы не перевернуть лодку! Что происходит с лодкой, когда вы добавляете четвертаки? Сколько четвертей нужно, чтобы потопить лодку?
- Подсчитайте, сколько граммов монет понадобилось, чтобы потопить лодку. Одна четверть имеет массу около 5,67 г.
- Сравните общую массу четверти с массой воды, которая наполняет лодку (из шага 2). Что вы заметили?
«Лодка» тонет, когда вес четвертаков превышает вес воды, наполняющей лодку.
Если все прошло хорошо, вы, наверное, заметили, что масса воды в полной чашке очень близка к массе четвертаков, необходимых для того, чтобы потопить лодку. Это не совпадение!
Лодка, плавающая в воде, ощущает две противодействующие силы: гравитацию, тянущую вниз, и нечто, называемое выталкивающей силой , толкающей вверх.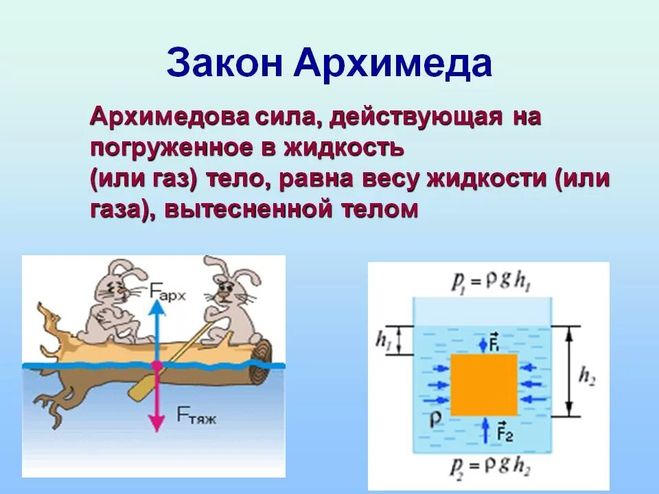 Выталкивающая сила возникает из-за разницы в давлении воды, воздействующей на лодку. Лодка всплывает, когда выталкивающая сила равна и противоположна весу лодки.
Выталкивающая сила возникает из-за разницы в давлении воды, воздействующей на лодку. Лодка всплывает, когда выталкивающая сила равна и противоположна весу лодки.
Объем воды, вытесненный лодкой, определяет выталкивающую силу. Лодка должна весить меньше или равна весу вытесненной воды, чтобы она могла плавать. Вы можете рассчитать выталкивающую силу на объем воды, умножив объем (в м 3 ), плотность воды (1000 кг/м 3 ) и ускорение свободного падения (9,8 м/с 2 ).
Когда вы наполнили лодку водой, вы вычислили массу максимального количества воды, которое она может вытеснить. Это говорит вам, насколько тяжелой может быть лодка, прежде чем она утонет. Затем вы опорожняете лодку и начинаете добавлять четвертак. Как только вес всех этих четвертей стал больше веса вытесненной воды, лодка затонула.
Камни тонут, потому что они весят больше, чем такой же объем воды. Авианосцы плавают, потому что, несмотря на то, что они невероятно массивны, на самом деле они весят меньше, чем количество воды, которую они вытесняют. Авианосцы подобны вашей пластиковой лодке, пока вы не добавили слишком много четвертей. Причина, по которой они весят меньше, сводится к одному: они менее плотны, чем вода . Корабли плавают, потому что они берут на себя вес всей этой стали и распределяют ее по очень большому объему. Авианосец на самом деле в основном заполнен воздухом!
Авианосцы подобны вашей пластиковой лодке, пока вы не добавили слишком много четвертей. Причина, по которой они весят меньше, сводится к одному: они менее плотны, чем вода . Корабли плавают, потому что они берут на себя вес всей этой стали и распределяют ее по очень большому объему. Авианосец на самом деле в основном заполнен воздухом!
Если вы возьмете корабль и превратите его в шар, он больше не будет плавать. Вы можете проверить это, взяв пустую банку из-под газировки и погрузив ее в воду. Затем раздавите банку и верните ее в воду. Несмотря на то, что он весит точно так же, как и раньше, он тонет! Это потому, что, раздавив его, вы увеличили плотность, и выталкивающая сила больше не могла его удерживать.
Заявление об отказе от ответственности и меры предосторожности
Education.com предоставляет идеи проекта научной ярмарки для ознакомления
только цели. Education. com не дает никаких гарантий или заявлений
com не дает никаких гарантий или заявлений
относительно идей проекта научной ярмарки и не несет ответственности за
любые убытки или ущерб, прямо или косвенно вызванные использованием вами таких
Информация. Получая доступ к идеям проекта научной ярмарки, вы отказываетесь и
отказаться от любых претензий к Education.com, возникающих в связи с этим. Кроме того, ваш
доступ к веб-сайту Education.com и проектным идеям научной ярмарки покрывается
Политика конфиденциальности Education.com и Условия использования сайта, включая ограничения
об ответственности Education.com.
Настоящим предупреждаем, что не все проектные идеи подходят для всех
отдельных лиц или во всех обстоятельствах. Реализация любой идеи научного проекта
следует проводить только в соответствующих условиях и с соответствующими родителями.
или другой надзор. Чтение и соблюдение мер предосторожности всех
материалы, используемые в проекте, является исключительной ответственностью каждого человека. За
дополнительную информацию см.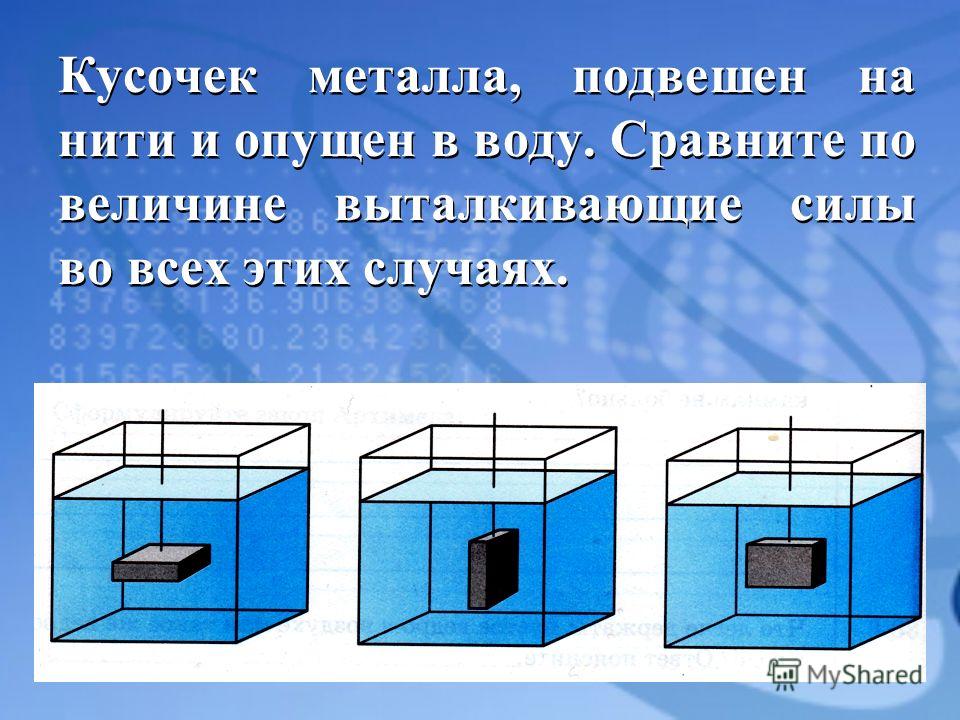 в справочнике по научной безопасности вашего штата.
в справочнике по научной безопасности вашего штата.
Принцип Архимеда и плавучесть – Университетская физика, том 1
Гидромеханика
Цели обучения
К концу этого раздела вы сможете:
- Определить выталкивающую силу
- Государственный закон Архимеда
- Опишите связь между плотностью и законом Архимеда
При помещении в жидкость некоторые объекты всплывают благодаря выталкивающей силе. Откуда берется эта выталкивающая сила? Почему одни вещи плавают, а другие нет? Получают ли объекты, которые тонут, какую-либо поддержку от жидкости? Ваше тело поддерживается атмосферой или это касается только гелиевых шаров ((Рисунок))?
(а) Даже объекты, которые тонут, как этот якорь, частично поддерживаются водой при погружении. (b) Подводные лодки имеют регулируемую плотность (балластные цистерны), так что они могут плавать или тонуть по желанию. (c) Воздушные шары, наполненные гелием, тянут вверх свои нити, демонстрируя плавучесть воздуха.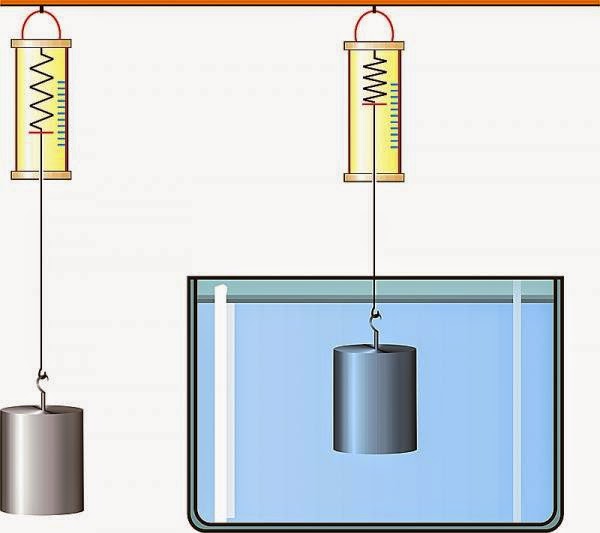 (кредит b: модификация работы Allied Navy; кредит c: модификация работы «Crystl»/Flickr)
(кредит b: модификация работы Allied Navy; кредит c: модификация работы «Crystl»/Flickr)
Ответы на все эти и многие другие вопросы основаны на том факте, что давление в жидкости увеличивается с глубиной. Это означает, что восходящая сила на нижней части объекта в жидкости больше, чем направленная вниз сила на верхней части объекта. На любой объект в любой жидкости действует восходящая сила или выталкивающая сила ((Рисунок)). Если выталкивающая сила больше веса предмета, предмет поднимается на поверхность и всплывает. Если выталкивающая сила меньше веса тела, то оно тонет. Если выталкивающая сила равна весу объекта, объект может оставаться подвешенным на своей текущей глубине. Выталкивающая сила всегда присутствует, независимо от того, плавает ли объект, тонет или подвешен в жидкости.
Выталкивающая сила
Выталкивающая сила — это направленная вверх сила, действующая на любой объект в любой жидкости.
Давление из-за веса жидкости увеличивается с глубиной, потому что [latex]p=hpg[/latex]. Это изменение давления и связанная с ним восходящая сила на дне цилиндра больше, чем направленная вниз сила на верхней части цилиндра. Различия в силе приводят к выталкивающей силе [латекс] {F} _ {\ текст {B}} [/латекс]. (Горизонтальные силы отменяются.)
Это изменение давления и связанная с ним восходящая сила на дне цилиндра больше, чем направленная вниз сила на верхней части цилиндра. Различия в силе приводят к выталкивающей силе [латекс] {F} _ {\ текст {B}} [/латекс]. (Горизонтальные силы отменяются.)
Закон Архимеда
Насколько велика выталкивающая сила? Чтобы ответить на этот вопрос, подумайте о том, что происходит, когда погруженный объект вынимают из жидкости, как показано на рисунке. Если бы объект не находился в жидкости, пространство, занимаемое объектом, было бы заполнено жидкостью, имеющей вес [латекс] {w} _ {\ text {fl}}. [/latex] Этот вес поддерживается окружающей жидкостью, поэтому выталкивающая сила должна равняться [латексу] {w} _ {\ text {фл}}, [/ латексу] весу жидкости, вытесненной объектом.
Закон Архимеда
Выталкивающая сила, действующая на объект, равна весу вытесняемой им жидкости. В форме уравнения принцип Архимеда выглядит следующим образом:
[латекс] {F} _ {\ text {B}} = {w} _ {\ text {fl}}, [/latex]
, где [латекс] {F} _{\text{B}}[/latex] — выталкивающая сила, а [latex]{w}_{\text{fl}}[/latex] — вес жидкости, вытесненной объектом.
Этот принцип назван в честь греческого математика и изобретателя Архимеда (ок. 287–212 гг. до н. э.), который сформулировал этот принцип задолго до того, как понятие силы стало общепризнанным.
(a) На объект, погруженный в жидкость, действует выталкивающая сила [латекс] {F} _ {\ text {B}}. [/latex] Если [латекс] {F} _ {\ text {B}}[ /латекс] больше веса объекта, объект поднимается. Если [латекс]{F}_{\text{B}}[/латекс] меньше веса объекта, объект тонет. (b) Если объект удаляется, он заменяется жидкостью, имеющей вес [латекс] {w} _ {\ text {fl}}. [/latex]. Поскольку этот вес поддерживается окружающей жидкостью, выталкивающая сила должна равняться вес вытесненной жидкости.
Принцип Архимеда относится к силе плавучести, которая возникает, когда тело полностью или частично погружено в жидкость. Сила, обеспечивающая давление жидкости, действует на тело перпендикулярно поверхности тела. Другими словами, сила давления внизу направлена вверх, а сила давления вверху направлена вниз; силы из-за давлений по бокам направлены внутрь тела.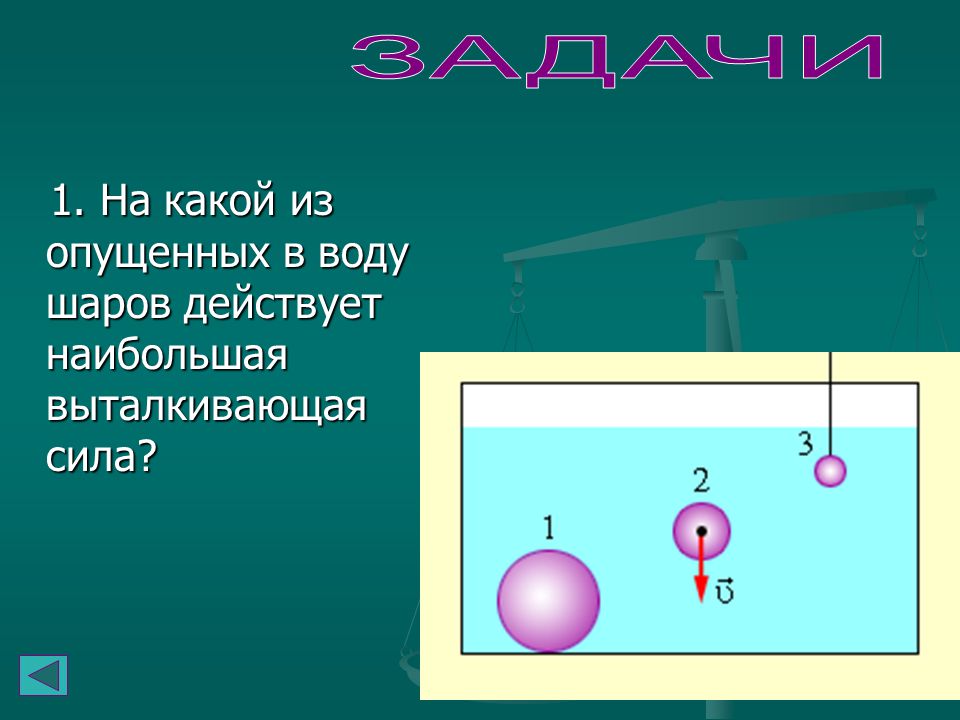
Поскольку нижняя часть корпуса находится на большей глубине, чем верхняя часть корпуса, давление в нижней части корпуса выше, чем давление в верхней части, как показано на (рис.). Следовательно, на тело действует направленная вверх сила. Эта направленная вверх сила есть сила плавучести, или просто плавучесть .
Восклицание «Эврика» (означающее «Я нашел это») часто приписывают Архимеду, когда он сделал открытие, которое привело к принципу Архимеда. Некоторые говорят, что все началось в ванной. Чтобы прочитать историю, посетите NASA или откройте журнал Scientific American, чтобы узнать больше.
Плотность и закон Архимеда
Если бросить в воду кусок глины, он утонет. Но если вы слепите из того же куска глины форму лодки, она будет плавать. Из-за своей формы глиняная лодка вытесняет больше воды, чем глыба, и испытывает большую выталкивающую силу, хотя ее масса одинакова. То же самое и со стальными кораблями.
Средняя плотность объекта определяет, будет ли он плавать. Если средняя плотность объекта меньше плотности окружающей жидкости, он будет плавать. Причина в том, что жидкость, имеющая более высокую плотность, содержит большую массу и, следовательно, больший вес в том же объеме. Таким образом, выталкивающая сила, равная весу вытесненной жидкости, больше веса объекта. Точно так же объект, более плотный, чем жидкость, утонет.
Если средняя плотность объекта меньше плотности окружающей жидкости, он будет плавать. Причина в том, что жидкость, имеющая более высокую плотность, содержит большую массу и, следовательно, больший вес в том же объеме. Таким образом, выталкивающая сила, равная весу вытесненной жидкости, больше веса объекта. Точно так же объект, более плотный, чем жидкость, утонет.
Степень погружения плавучего объекта зависит от того, как плотность объекта соотносится с плотностью жидкости. На (Рисунок), например, незагруженный корабль имеет меньшую плотность и меньше его погружено по сравнению с тем же кораблем, когда он загружен. Мы можем получить количественное выражение для фракции, погруженной в воду, учитывая плотность. Погруженная доля представляет собой отношение погруженного объема к объему объекта, или
[латекс] \ text {фракция погружена} = \ frac {{V} _ {\ text {sub}}} {{V} _ {\ text {obj}}} = \ frac {{V} _ {\ text{fl}}}{{V}_{\text{obj}}}.[/latex]
Погруженный объем равен объему вытесненной жидкости, которую мы называем [латекс]{V}_{fl}[ /латекс]. Теперь мы можем получить связь между плотностями, подставив в выражение [латекс]\ро =\фрак{м}{В}[/латекс]. Это дает
Теперь мы можем получить связь между плотностями, подставив в выражение [латекс]\ро =\фрак{м}{В}[/латекс]. Это дает
[латекс]\frac{{V}_{\text{fl}}}{{V}_{\text{obj}}}=\frac{{m}_{\text{fl}} \text{/}{\rho} _{\text{fl}}}{{m}_{\text{obj}}\text{/}{\rho}_{\text{obj}}},[ /латекс]
, где [latex]{\rho }_{\text{obj}}[/latex] — средняя плотность объекта, а [latex]{\rho }_{\text{fl}}[/latex] — плотность жидкости. Поскольку объект плавает, его масса и масса вытесненной жидкости равны, поэтому они исключаются из уравнения, в результате чего остается
[латекс]\текст{фракция под водой}=\фракция{{\rho} _{\текст{объект} }}{{\rho }_{\text{fl}}}.[/latex]
Мы можем использовать это соотношение для измерения плотности.
Незагруженное судно (а) плавает выше в воде, чем загруженное судно (б).
Расчет средней плотности
Предположим, что женщина массой 60,0 кг плавает в пресной воде, при этом 97,0% ее объема погружено в воду, когда ее легкие наполнены воздухом.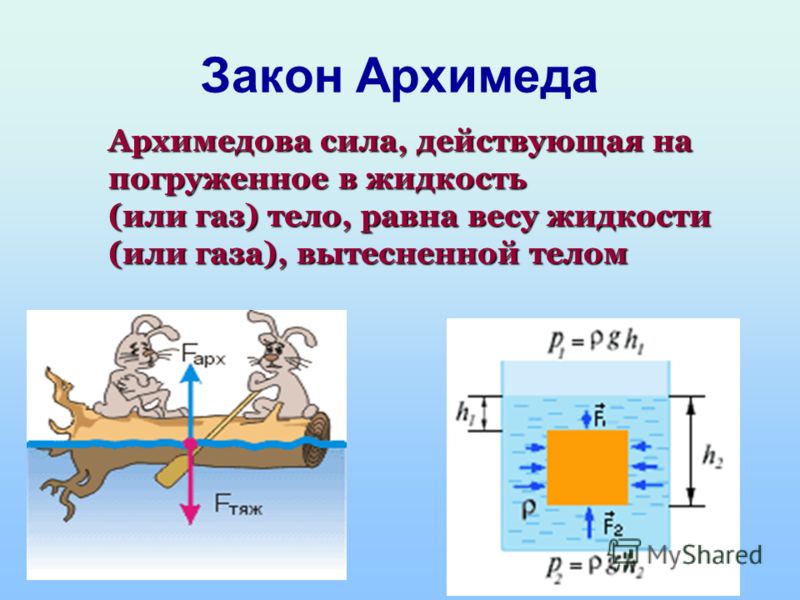 Какая у нее средняя плотность?
Какая у нее средняя плотность?
Стратегия
Мы можем найти плотность женщины, решив уравнение text{fl}}}[/latex]
для плотности объекта. Это дает
[латекс] {\ rho } _ {\ text {obj}} = {\ rho } _ {\ text {person}} = \ text {(фракция погружена)} · {\ rho } _ {\ text {фл}}.[/латекс] 9{3}}.[/latex]
Значение
Плотность женщины меньше плотности жидкости. Мы ожидаем этого, потому что она плавает.
Многочисленные объекты или вещества с более низкой плотностью плавают в жидкостях с более высокой плотностью: масло на воде, воздушный шар в атмосфере, кусочек пробки в вине, айсберг в соленой воде и горячий воск в «лавовой лампе». ,» назвать несколько. Менее очевидный пример — горные хребты, плавающие на более плотной коре и мантии под ними. Даже кажущаяся твердой Земля обладает жидкими характеристиками.
Измерение плотности
Один из наиболее распространенных методов определения плотности показан на (Рисунок).
(a) Монета взвешивается в воздухе.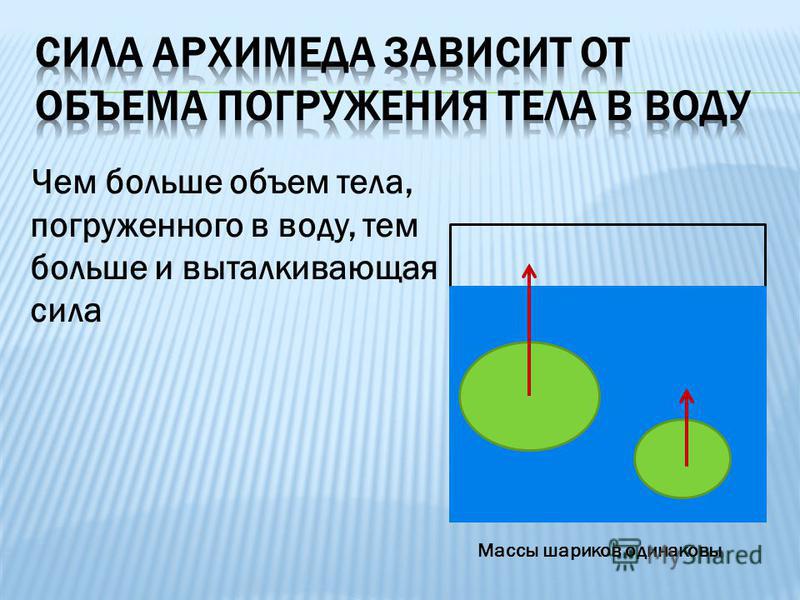 (b) Определяется кажущийся вес монеты, когда она полностью погружена в жидкость известной плотности. Эти два измерения используются для расчета плотности монеты.
(b) Определяется кажущийся вес монеты, когда она полностью погружена в жидкость известной плотности. Эти два измерения используются для расчета плотности монеты.
Предмет, здесь монета, взвешивается в воздухе, а затем снова взвешивается, погруженный в жидкость. Плотность монеты, показатель ее подлинности, можно рассчитать, если известна плотность жидкости. Мы можем использовать этот же метод для определения плотности жидкости, если известна плотность монеты.
Все эти расчеты основаны на принципе Архимеда, согласно которому выталкивающая сила, действующая на объект, равна весу вытесненной жидкости. Это, в свою очередь, означает, что погруженный в воду объект кажется менее весящим; мы называем это измерение кажущимся весом объекта. Объект испытывает кажущуюся потерю веса, равную весу вытесненной жидкости. В качестве альтернативы, на весах, измеряющих массу, объект испытывает кажущуюся потерю массы, равную массе вытесненной жидкости. То есть кажущаяся потеря веса равна массе вытесненной жидкости, или кажущаяся потеря массы равна массе вытесненной жидкости.
Резюме
- Выталкивающая сила — это результирующая восходящая сила, действующая на любой объект в любой жидкости. Если выталкивающая сила больше веса объекта, объект поднимется на поверхность и всплывет. Если выталкивающая сила меньше веса тела, то оно утонет. Если выталкивающая сила равна весу объекта, объект может оставаться подвешенным на своей текущей глубине. Выталкивающая сила всегда присутствует и действует на любой объект, частично или полностью погруженный в жидкость.
- Принцип Архимеда гласит, что выталкивающая сила, действующая на объект, равна весу вытесняемой им жидкости.
Концептуальные вопросы
Чтобы вытащить пробку из полной ванны, требуется больше усилий, чем когда она пуста. Противоречит ли это принципу Архимеда? Поясните свой ответ.
Вовсе нет. Принцип Паскаля гласит, что изменение давления осуществляется через жидкость. Причина, по которой полная ванна требует большего усилия, чтобы вытащить пробку, заключается в весе воды над пробкой.
Оказывают ли жидкости выталкивающую силу в «невесомой» среде, например, в космическом челноке? Поясните свой ответ.
Будет ли один и тот же корабль плавать выше в соленой воде, чем в пресной? Поясните свой ответ.
Выталкивающая сила равна весу вытесненной жидкости. Чем больше плотность жидкости, тем меньше жидкости необходимо вытеснить, чтобы удерживать вес объекта и плавать. Поскольку плотность соленой воды выше, чем плотность пресной воды, меньше соленой воды будет вытеснено, и корабль будет плавать выше. 9{3}[/латекс]?
а. погружено на 99,5 %; б. 96,9% под водой
Камень массой 540 г в воздухе имеет кажущуюся массу 342 г при погружении в воду. а) Какая масса воды вытесняется? б) Каков объем камня? в) Какова его средняя плотность? Соответствует ли это стоимости гранита?
Принцип Архимеда можно использовать для расчета плотности жидкости и твердого тела. Предположим, что кусок железа массой 390,0 г в воздухе имеет кажущуюся массу 350,5 г, когда он полностью погружен в неизвестную жидкость. а) Какую массу жидкости вытесняет железо? б) Чему равен объем железа, если использовать его плотность, указанную на (рис.)? в) Рассчитайте плотность жидкости и определите ее. 9{3}[/латекс]; этиловый спирт
а) Какую массу жидкости вытесняет железо? б) Чему равен объем железа, если использовать его плотность, указанную на (рис.)? в) Рассчитайте плотность жидкости и определите ее. 9{3}[/латекс]; этиловый спирт
Рассчитайте выталкивающую силу 2-литрового гелиевого баллона. (b) Учитывая, что масса резины в воздушном шаре составляет 1,50 г, какова результирующая вертикальная сила, действующая на воздушный шар, если его отпустить? Объемом резины пренебречь.
Какова плотность женщины, плавающей в пресной воде с [латексом]4,00\текст{%}[/латекс] ее объема над поверхностью? (Это можно измерить, поместив ее в резервуар с отметками на боку, чтобы измерить, сколько воды она вытесняет, когда плавает и удерживается под водой.) (b) Какой процент ее объема находится над поверхностью, когда она плавает в морской воде? 9{3}[/latex] (за исключением воздуха в легких). а) Вычислите его объем. б) Найдите выталкивающую силу воздуха, действующую на него. в) Каково отношение выталкивающей силы к его весу?
Простой компас можно сделать, поместив небольшой стержневой магнит на пробку, плавающую в воде. а) Какая часть простой пробки окажется под водой, когда она будет плавать в воде? б) Если пробка массой 10,0 г поместить на нее магнит массой 20,0 г, какая часть пробки окажется под водой? в) Будут ли стержневой магнит и пробка плавать в этиловом спирте?
а) Какая часть простой пробки окажется под водой, когда она будет плавать в воде? б) Если пробка массой 10,0 г поместить на нее магнит массой 20,0 г, какая часть пробки окажется под водой? в) Будут ли стержневой магнит и пробка плавать в этиловом спирте?
а. 0,24; б. 0,68; в. Да, пробка будет плавать в этиловом спирте.
Какой процент веса железного якоря будет поддерживаться выталкивающей силой при погружении в соленую воду?
Ссылаясь на (рисунок), докажите, что выталкивающая сила, действующая на цилиндр, равна весу вытесненной жидкости (принцип Архимеда). Вы можете предположить, что выталкивающая сила равна [латекс]{F}_{2}-{F}_{1}[/латекс] и что концы цилиндра имеют равные площади[латекс]А[/латекс]. Обратите внимание, что объем цилиндра (и объем вытесняемой им жидкости) равен [латекс]\left({h}_{2}-{h}_{1}\right)A[/latex].
[латекс]\begin{array}{ccc}\text{net}\phantom{\rule{0.2em}{0ex}}F\hfill & =\hfill & {F}_{2}-{F} _{1}={p}_{2}A-{p}_{1}A=\left({p}_{2}-{p}_{1}\right)A=\left({ h}_{2}{\rho}_{\text{fl}}g-{h}_{1}{\rho}_{\text{fl}}g\right)A\hfill \\ & = \hfill & \left({h}_{2}-{h}_{1}\right){\rho}_{\text{fl}}gA,\phantom{\rule{0.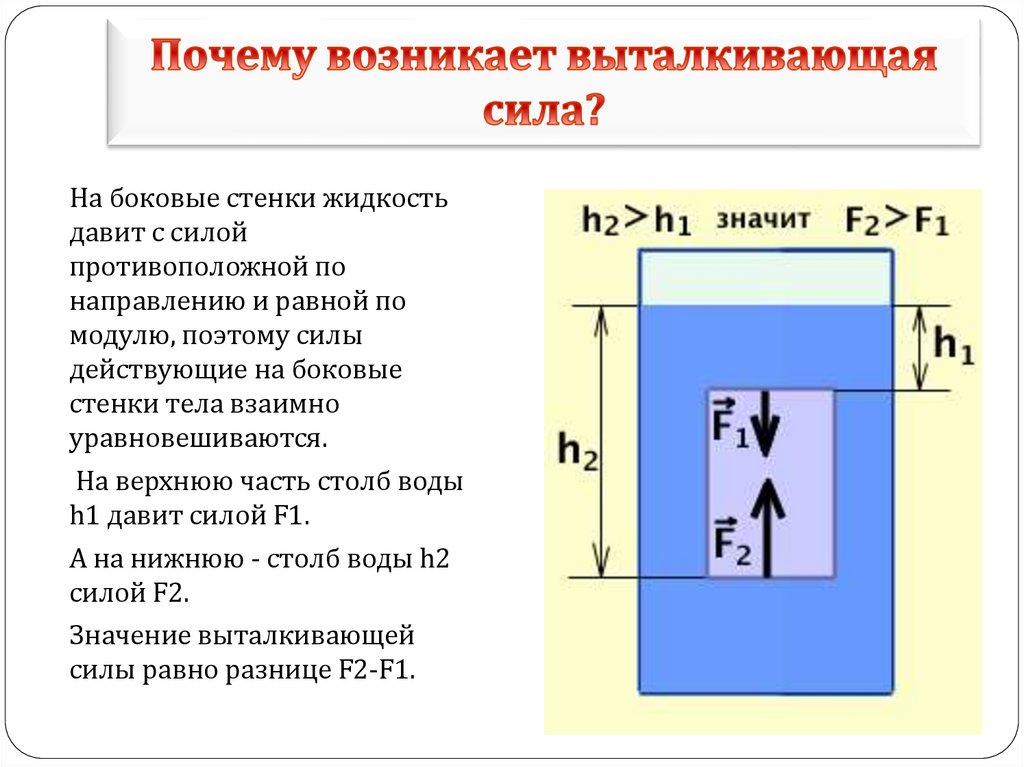


 Судно утонет.
Судно утонет.
 Количество воды в лодке говорит о ее объеме.
Количество воды в лодке говорит о ее объеме.