Ребусы про воду: Ребус вода для детей с ответом онлайн

Содержание

Ребус вода для детей с ответом онлайн

Есть идеи или пожелания?

Главная
 Статьи детям и родителям
 Детское развитие
 Детские ребусы
 Ребус вода

Июнь 20

Ответ

Kindbi

Экологические ребусы

Школьные ребусы

Ребусы с цифрами

Ребусы с нотами

Ребусы птицы

Ребусы профессии

Ребусы про животных

Ребусы по химии

Ребусы по физике

Ребусы по сказкам

Нашли ошибку? Ctrl+Enter

Самые интересные загадки про воду с ответами

Домашняя /

Загадки для детей /

Про воду

Загадки про воду рассказывают детям в игровой форме о всем ее многообразии, о реках, озерах, океанах. Она может быть жидкой, твердой и газообразной. Вода превращается в состояние льда при температуре 0 градусов Цельсия, а закипает — при 100 градусах. Объем пресной воды составляет всего лишь 3% от всего объема, содержащегося на Земле. Без еды человек способен прожить в течение 30 дней, а без воды может продержаться только 3-4 дня.

Разгадывать загадки о воде и запоминать их достаточно легко. Дети с радостью пытаются отгадать загадку, окунаясь в удивительный водный мир, познавая интересные факты, как о самой воде, так и о животном и растительном мире, населяющем реки, озера и океаны.

•Много меня — пропал бы мир,

Мало меня — пропал бы мир

(Вода)

•Книзу летит капельками,

А кверху — невидимкою.

(Вода)

•В жаркий день

Самой желанной бывает.

(Вода)

•Я и туча, и туман,

И ручей, и океан,

И летаю, и бегу,

И стеклянной быть могу!

(Вода)

•Чего в гору не выкатить,

В решете не унести

И в руках не удержать?

(Вода)

•В морях и реках обитает,

Но часто по небу летает.

А как наскучит ей летать,

На землю падает опять.

(Вода)

•Не конь, а бежит,

Не лес, а шумит.

(Река)

•Течет, течет —

Не вытечет,

Бежит, бежит-

Не выбежит.

(Река)

•Зимой спит,

А летом шумит.

(Река)

•Нет ног, но на месте она не стоит,

Ложе есть, но не спит,

Не котел, но бурлит,

Не гроза, но гремит.

Нет рта, но она никогда не молчит.

(Река)

•Если руки наши в ваксе,

Если на нос сели кляксы,

Кто тогда нам первый друг,

Снимет грязь с лица и рук?

Без чего не может мама

Ни готовить, ни стирать,

Без чего, мы скажем прямо,

Человеку умирать?

Чтобы лился дождик с неба,

Чтоб росли колосья хлеба,

Чтобы плыли корабли —

Жить нельзя нам без . ..

(Воды)

•Не море, не земля,

Корабли не плавают,

А ходить нельзя.

(Болото)

•В нее льется, из нее льется, сама по земле плетется.

(Река)

•Кругом вода, а с питьем беда.

(Море)

•По городу дождик осенний гулял,

Зеркальце дождик свое потерял.

Зеркальце то на асфальте лежит,

Ветер подует — оно задрожит.

(Лужа)

•Что за звездочки сквозные на пальто и на платке.

Все сквозные, вырезные, а возьмешь — вода в руке?

(Снежинка)

•Посреди поля лежит зеркало:

стекло голубое, рама зеленая.

(Пруд)

← Предыдущая Загадки про природу

Вы прочитали: Загадки про воду

→ Следующая Загадки про радугу

Выливание воды и головоломки с взвешиванием

Выливание воды I

Если бы у вас была 5-литровая и 3-литровая миска и неограниченный доступ к воде, как бы вы отмерили ровно 4 литра?

Проливная вода II

Даны три миски: на 8, 5 и 3 литра, разделите 8 литров пополам (4 + 4 литра) с минимальным количеством переливаний воды. Обратите внимание, что 8-литровая чаша изначально заполнена 8 литрами воды, а две другие чаши пусты — это вся вода, которая у вас есть.

Обливание водой III

Дано три миски: 7, 4 и 3 литра вместимостью. Только 7-литровый полный. Наливая воду наименьшее количество раз, сделайте объемы 2, 2 и 3 литра.

Обливание водой IV

Как можно отмерить 6 литров воды, используя только 4- и 9-литровые миски?

Проливная вода V

Отмерьте ровно 2 литра воды, если у вас есть:
1. Стакан 4 и 5 литров
2. 4-х и 3-х литровый стакан

Проливная вода VI

Даны три миски: миска А (вместимостью 8 литров), наполненная 5 литрами воды; чаша B (вместимость 5 литров), наполненная 3 литрами воды; и чаша C (вместимостью 3 литра), наполненная 2 литрами воды.
Сможете ли вы отмерить ровно 1 литр, перелив воду всего 2 раза?

Взвешивание I

У вас есть 10 мешков по 1000 монет в каждом. В одном из мешков все монеты фальшивые. Настоящая монета весит 1 грамм; каждая фальшивая монета весит 1,1 грамма.
Если у вас есть точные весы, которые вы можете использовать только один раз, как вы сможете идентифицировать сумку с подделками? А что, если бы вы не знали, сколько мешков с фальшивыми монетами?

Взвешивание II

Настоящий мармеладный мишка имеет массу 10 грамм, а искусственный мармеладный мишка — 9 грамм. У Спайка 7 коробок мармеладных мишек, 4 из которых настоящие мармеладные мишки, а остальные — имитация.
Используя весы только один раз и минимальное количество мармеладных мишек, как Спайк может определить, в каких коробках находятся настоящие мармеладные мишки?

Взвешивание III

Эта головоломка идет на шаг дальше от предыдущей.
У вас есть восемь мешков, в каждом из которых по 48 монет. В пяти из этих мешков только настоящие монеты, в остальных — фальшивые. Поддельная монета весит на 1 грамм меньше, чем настоящая монета. У вас есть точные весы, с точностью до 1 грамма.
Взвесив только один раз и используя минимальное количество монет, как найти мешки с фальшивыми монетами?

Взвешивание IV

Один из двенадцати теннисных мячей немного легче или тяжелее (вы не знаете, что именно), чем остальные. Как бы вы определили этот странный шар, если бы вы могли использовать старые весы с двумя чашами только 3 раза?
Вы можете сбалансировать только один набор шаров с другим, поэтому никаких эталонных весов и никаких измерений веса.

Взвешивание В

На елке было два синих, два красных и два белых шара. Все казалось одинаковым. Однако в каждой цветовой паре один шар был тяжелее. Все три более легких шара весили одинаково, как и все три более тяжелых.
Используя весы дважды, определите более легкие шары.

Взвешивание VI

Есть 9подобные мячи. Восемь из них весят одинаково, а девятый немного тяжелее.
Как бы вы определили более тяжелый мяч, если бы вы могли использовать весы с двумя чашами только дважды?

Взвешивание VII

Из 27 мячей для настольного тенниса один тяжелее другого.
Какое минимальное количество взвешиваний (на двухчашечных весах) необходимо для гарантированного определения тяжелого? Конечно, остальные 26 шаров весят столько же.

Взвешивание VIII

Предположим, что объекты, подлежащие взвешиванию, могут иметь вес от 1 до 121 фунта с интервалом в 1 фунт: 1, 2, 3,.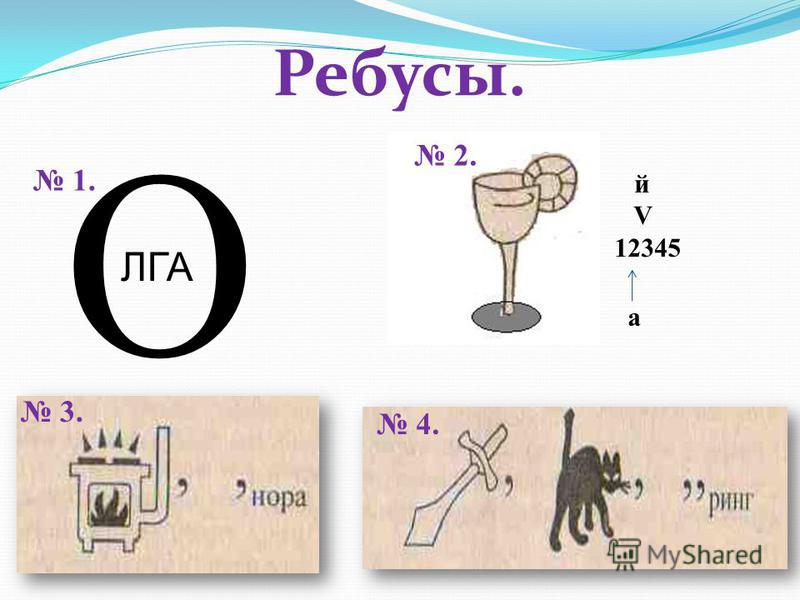 .., 119, 120 и 121. После помещения одной такой гири на любую из двух чашек весов пары весов, затем одну или несколько предварительно откалиброванных гирь помещают в одну или обе чаши до тех пор, пока не будет достигнут баланс, таким образом определяя вес объекта.
Если относительное положение рычага, точки опоры и тарелок нельзя изменить и нельзя добавить к исходному набору предварительно откалиброванных гирь, то какое минимальное количество таких гирь было бы достаточно, чтобы привести в равновесие любую из этих гирь? 121 возможных объектов?

Песочные часы I

Имея 2 песочных часа: одни 7-минутные, а вторые 4-минутные, как правильно отсчитать 9 минут?

Песочные часы II

Учитель математики использовал нетрадиционный метод для измерения 15-минутного лимита времени на тест. Он просто использовал 7-минутные и 11-минутные песочные часы. За все время он перевернул песочные часы только 3 раза (одновременное переворачивание обоих песочных часов считается одним подбрасыванием).
Объясните, как учитель отмерил 15 минут.

Горящие предохранители

Ваша задача — отмерить 45 минут, если у вас есть только два шнура и спички, чтобы зажечь шнуры.

Два шнура скручены из разных материалов, поэтому их разные сегменты могут гореть с разной скоростью.
Каждый шнур прогорает от начала до конца ровно за час.

Поделитесь этой страницей с друзьями

Узнайте больше о математических головоломках >>

Головоломка с кувшином для воды

FutureLearn использует куки-файлы для повышения удобства пользования веб-сайтом. Все файлы cookie, кроме строго необходимых, в настоящее время отключены для этого браузера. Включите JavaScript, чтобы применить настройки файлов cookie для всех необязательных файлов cookie. Вы можете ознакомиться с политикой FutureLearn в отношении файлов cookie здесь.

Йосси Эльран рассказывает нам о головоломке с кувшином для воды

Вот еще одна хорошо известная средневековая задача, также известная как «головоломка с выливанием воды».

У вас есть 8-литровый кувшин с водой и два меньших кувшина, в одном 5 литров, а в другом 3 литра. Ни на одном из кувшинов нет маркировки, и у вас нет дополнительного измерительного прибора. Вы должны разделить 8 литров воды поровну между двумя вашими лучшими друзьями так, чтобы каждый получил по 4 литра воды. Как вы можете это сделать?

Подождите! Попробуйте решить эту головоломку, прежде чем читать дальше.

Головоломка с кувшином для воды – решение

Сначала вода переливается из 8-литрового кувшина в 5-литровый кувшин, в исходном 8-литровом кувшине остается 3 литра воды.
Затем вода переливается из 5-литрового кувшина в 3-литровый кувшин, так что теперь у нас есть 3 литра воды в 8-литровом кувшине, 2 литра воды в 5-литровом кувшине и 3 литра воды в 3-литровом кувшине. .
3-литровый кувшин переливается в 8-литровый кувшин, поэтому 8-литровый кувшин теперь содержит 6 литров воды.
Теперь 2 литра воды из 5-литрового кувшина переливаются в пустой 3-литровый кувшин.
Вода переливается из 8-литрового кувшина (который на данном этапе содержит 6 литров) в пустой 5-литровый кувшин.
Теперь у нас есть 5 литров воды в 5-литровом кувшине, 2 литра воды в 3-литровом кувшине и 1 литр воды в 8-литровом кувшине.
Вода выливается из 5-литрового кувшина, чтобы наполнить 3-литровый кувшин, который на данном этапе уже содержит 2 литра воды.
У нас осталось 4 литра воды в 5-литровом кувшине, который дают одному другу, и 3 литра воды в 3-литровом кувшине, который переливается обратно в 8-литровый кувшин, в котором уже содержится 1 литр воды. Это дает 4 литра воды, которые отдаются второму другу.

Весь сценарий можно резюмировать, используя числа в скобках, обозначающие количество литров воды на каждом этапе в каждом из 8-литровых, 5-литровых и 3-литровых кувшинов соответственно:

[[8,0,0] стрелка вправо [3,5,0] стрелка вправо [3,2,3] стрелка вправо [6,2,0] стрелка вправо [6,0,2] стрелка вправо [1,5,2] стрелка вправо [1,4,3] стрелка вправо [4,4,0]]

Эта диаграмма известна как диаграмма состояний

Проблема с кувшином для воды может быть решена с помощью всего двух кувшинов – одного на 5 литров воды, а другого на 3 литра воды, если есть также неограниченный запас воды из крана и раковины. Покажите ряд диаграмм состояний, решающих эту задачу. Пишите свои решения в комментариях!

Эта статья взята из бесплатного онлайн-ресурса

Введение в рекреационную математику: развлечения, игры и головоломки

Создано

Присоединяйся сейчас