Содержание
Как вычислить объем воды в трубе
Главная » Разное » Как вычислить объем воды в трубе
Калькулятор объема трубы онлайн
Для расчета объема трубы введите в калькулятор внутренний диаметр (в миллиметрах) и длину трубы (в метрах). В результате вы увидите полный объем и объем погонного метра, как в метрах кубических, так и в литрах.
Объем трубы важен при расчете систем отопления, газопроводов и водопроводов. Так же при строительстве скважин и колодцев.
Поделитесь с друзьями в соцсетях…
Похожие калькуляторы:
Раздел: Строительные калькуляторы
Трубы — Содержание воды — Вес и объем
| Размер трубы (внутренний диаметр) (дюйм) | Содержание воды | |||
|---|---|---|---|---|
| Объем | Вес (фунт / фут) | Объем / вес | ||
| (дюймы 3 / фут) | (галлоны / фут) | (литры / м, кг / м) | ||
| 1 / 4 | 0. 59 | 0,003 | 0,02 | 0,030 |
| 3/8 | 1,33 | 0,006 | 0,05 | 0,074 |
| 1/2 | 2,36 | 0,010 | 0,09 | 0,13 |
| 3/4 | 5,30 | 0,023 | 0,19 | 0,28 |
| 1 | 9,43 | 0,041 | 0,34 | 0,51 |
| 1 1/4 | 14.7 | 0,064 | 0,53 | 0,79 |
| 1 1/2 | 21,2 | 0,092 | 0,77 | 1,1 |
| 2 | 37,7 | 0,163 | 1,36 | 2,0 |
| 2 1/2 | 58,9 | 0,255 | 2,13 | 3,2 |
| 3 | 84,8 | 0,367 | 2,31 | 3,4 |
| 4 | 150.8 | 0,653 | 5,44 | 8,1 |
| 5 | 235,6 | 1,02 | 8,50 | 13 |
| 6 | 339,3 | 1,47 | 12,2 | 18 |
| 603,2 | 2,61 | 21,8 | 32 | |
| 10 | 942,5 | 4,08 | 34,0 | 51 |
| 12 | 1357. 2 | 5,88 | 49,0 | 73 |
| 15 | 2120,6 | 9,18 | 76,5 | 114 |
- 1 фунт / фут = 1,49 кг / м
- 1 США) / фут = 12,4 л / м
Обратите внимание, что для большинства труб номинальный размер не равен внутреннему диаметру. Для получения точных объемов — проверьте документацию на трубы или стандарт — и используйте калькулятор ниже.
Объемный вес для других жидкостей может быть рассчитан с учетом плотности.
Пример — содержание воды в трубе
Объем воды в трубе 12 м длиной 2 дюйма можно рассчитать как
(2,0 л / м) (12 м)
= 24 литра
Трубы — Калькулятор объема
Этот калькулятор можно использовать для расчета объема воды или других жидкостей в трубах. Калькулятор является универсальным и может использоваться для любых единиц, если единицы измерения согласованы.
Если введено м результат м 3 / м и так далее.
Внутренний диаметр трубы (м, мм, фут, дюйм …)
Используйте конвертер объема в левом столбце для других единиц.
.
Как найти объем с помощью метода вытеснения воды
Наука учит мыслить нестандартно. Таким образом, в то время как другие могут использовать воду только для питья и купания, мы научимся использовать ее для определения объема объекта.
Даже Ворона его использует!
Помните старую басню Эзопа «Ворона и кувшин»? В нем ворона может поднимать уровень воды, бросая камни в кувшин. На самом деле это очень хорошее практическое применение метода вытеснения воды.
Хотите написать для нас? Что ж, мы ищем хороших писателей, которые хотят распространять информацию. Свяжитесь с нами, и мы поговорим …
Давайте работать вместе!
Представьте себе мир, состоящий только из цилиндров, конусов, кубов и сфер.
Как легко было бы применить математику в таком обычном и четко определенном месте, как это! Например, все, что вам нужно сделать, это запомнить набор из четырех формул, и вы легко сможете узнать объем чего угодно.Но прежде чем попросить создателя пересмотреть Его замысел, спросите себя, действительно ли вы хотели бы жить в таком месте?
Плавные изгибы и случайные края различных предметов вокруг нас — это именно то, что делает их такими красивыми. Мир со всеми его неровностями идеален таким, какой он есть. И чтобы жить здесь, нам не нужно жертвовать математикой, благодаря одному замечательному древнегреческому мыслителю и изобретателю Архимеду.
Среди множества замечательных изобретений Архимеда есть то, что сегодня известно как метод вытеснения воды.Его можно использовать для точного расчета объема любого объекта, независимо от его формы, и, что самое приятное, он также не требует каких-либо сложных математических вычислений. Это так же просто, как и гениально. В следующих разделах мы узнаем, как это работает.
Но перед этим давайте сначала посмотрим, как великий Архимед пришел к этой идее.
История изобретения
Архимед жил в Сиракузах, Греция, более 2000 лет назад. Он был физиком, математиком, инженером и астрономом.Сказания о его мудрости и гении были хорошо известны по всей стране.
У короля Сиракуз была золотая корона, сделанная одним из лучших ювелиров в его королевстве. Сам король предоставил необходимое для этого чистое золото. Ювелир проделал прекрасную работу по изготовлению короны, но царь подозревал, что он фальсифицировал чистое золото серебром. Однако, поскольку в то время не было средств проверки чистоты металла, утверждение ювелира не могло быть проверено. Царь вызвал Архимеда и поручил ему проверить подлинность золотой короны, но не разрушить ее.
Это был настоящий вызов! Архимед работал много дней, испробовал все известные методы и применил все свои математические знания; однако он просто не мог придумать решения. Однажды, все еще борясь с проблемой, Архимед решил принять успокаивающую ванну, чтобы очистить голову.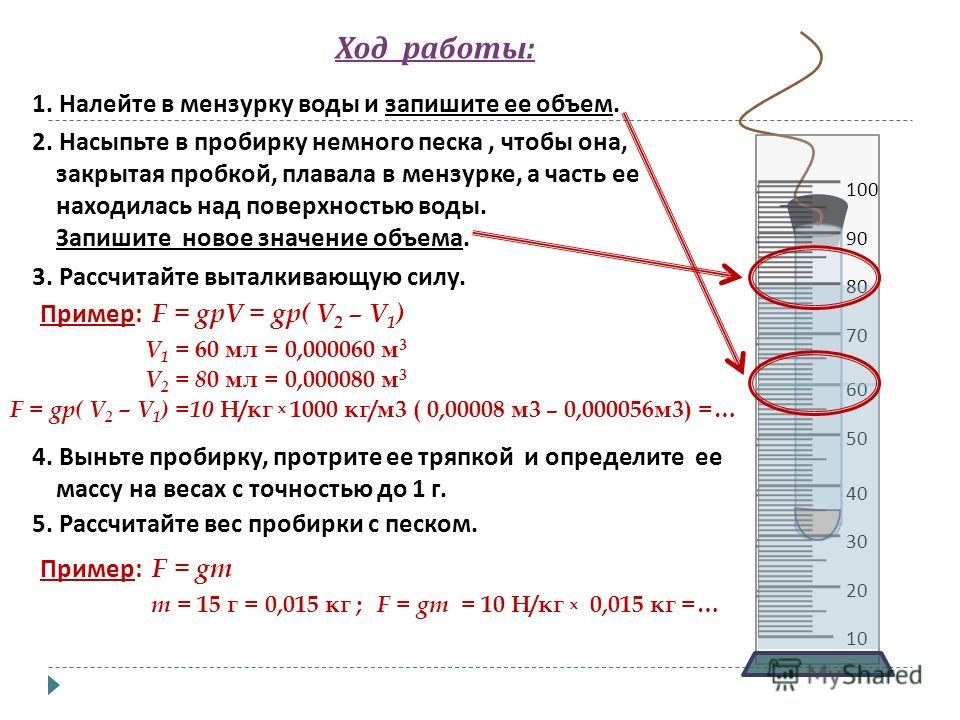
Он наполнил ванну водой и приготовил для него.
Когда Архимед вошел в полную ванну, он заметил, что из нее выплеснулось немного воды. Когда он погрузил в воду большую часть своего тела, вылилось еще больше воды.Он сразу понял, что нашел решение проблемы короля.
Он был так взволнован, что спрыгнул с ванны и побежал по улицам совершенно голый, крича «Эврика, Эврика !!!». Он представил свои результаты королю, используя которые, король смог доказать, что ювелир действительно обманул ему, добавив серебра в корону.
Хотите написать для нас? Что ж, мы ищем хороших писателей, которые хотят распространять информацию. Свяжитесь с нами, и мы поговорим…
Давайте работать вместе!
Сегодня метод Архимеда известен как метод вытеснения воды и широко используется благодаря своей простоте и точности.
Как работает метод
Так как же Архимед смог проверить изготовление короны, наблюдая за переливом воды из своей ванны?
Когда Архимед вошел в ванну и увидел, что вода в ней перелилась, он сразу понял, что между этими двумя событиями существует какая-то связь.
Когда он погрузился глубже и увидел, что вода вышла через край, он сразу понял, что связь между его массой и массой переливающейся воды была прямой.
Он понял, что если корону полностью погрузить в воду и измерить точное количество воды, которая в результате переливается, то оно будет равно объему короны. Как только объем известен, можно рассчитать его плотность, то есть массу, деленную на объем.
Плотность короны была бы ниже, чем у чистого золота, если бы к ней был добавлен более дешевый и менее плотный металл, такой как серебро.Таким образом, это была тщательная проверка, с помощью которой Архимед смог доказать фальшь ювелира.
Метод вытеснения воды можно использовать для точного определения объема объекта любой формы. По сути, он основан на том факте, что для всех практических целей вода несжимаема. Поэтому, когда объект попадает в воду, находящуюся в контейнере, вода вытесняется, чтобы освободить для него место. Таким образом, при полном погружении объект вытесняет объем воды, который точно равен его собственному объему.
Плавучесть: При падении в воду некоторые предметы имеют тенденцию тонуть, а другие плавать. Архимед понял причину этого и сформулировал принцип, объясняющий это, известный сегодня как принцип Архимеда.
Принцип Архимеда: Любой объект, полностью или частично погруженный в жидкость, поднимается вверх с силой, равной весу жидкости, которую этот объект вытесняет.
Таким образом, если объект вытесняет большую массу жидкости, он будет плавать, иначе он утонет.Большие корабли, хотя и очень тяжелые, могут плавать, поскольку вытесняют несколько тонн воды. С другой стороны, маленький камень намного легче по весу. Однако он все равно тонет, потому что способен вытеснить лишь небольшой вес воды.
Как найти том
Метод вытеснения воды Архимеда — один из самых удобных и простых способов измерения объема объекта неправильной формы. И вам не нужна ванна, чтобы он работал! Как вы увидите, вы можете практически применить этот метод с помощью всего лишь небольшого количества базового оборудования, выполнив следующие шаги.
Требования:
- Необычный объект.
- Градуированная цилиндрическая мерная колба, достаточно большая, чтобы в нее поместился объект.
- Блокнот и калькулятор.
Примечание. Показания мерной колбы указаны в мл.
Процедура:
- Заполните мерную колбу достаточным количеством воды.Основная идея здесь в том, чтобы не заливать его выше самой верхней отметки. Хороший способ обеспечить это — наполнить фляжку только наполовину, оставив достаточно отметок над уровнем воды.
- Когда вода уляжется, прочтите отметку внизу мениска, то есть изогнутую линию уровня воды. Это начальный объем воды внутри мерной колбы. Запишите его как «Vol1». В нашем примере начальный уровень воды составляет 13,33 мл. Таким образом, Vol1 = 13,33 мл .
- Теперь возьмите необычный предмет, объем которого вы хотите измерить, и осторожно опустите его в колбу.Подождите, пока вода осядет, и обратите внимание на отметку, соответствующую поднявшемуся уровню воды.
Это объем воды плюс объем объекта «Vol2». В нашем примере Vol2 = 30 мл . - Теперь используйте следующую формулу для вычисления объема объекта.
Это объем воды плюс объем объекта «Vol2». В нашем примере Vol2 = 30 мл . Объем (объект) = Объем (вода + объект) — Объем (вода)
Объем (объект) = Объем 2 — Объем 1
Объем (объект) = (30 — 13.33)
Объем (объект) = 16,66 мл.
Как только вы поймете шаги, показанные выше, попробуйте решить примеры, чтобы лучше понять метод вытеснения воды для расчета объема.
Примечание. Размеры мерной колбы указаны в мл.
Пример 1
Пример 2
Пример 3
Как найти плотность
Архимед смог рассчитать плотность короны с помощью метода вытеснения воды.Мы тоже можем рассчитать плотность любого объекта неправильной формы, используя шаги, указанные ниже.
1) Найдите объем объекта, как описано в предыдущем разделе.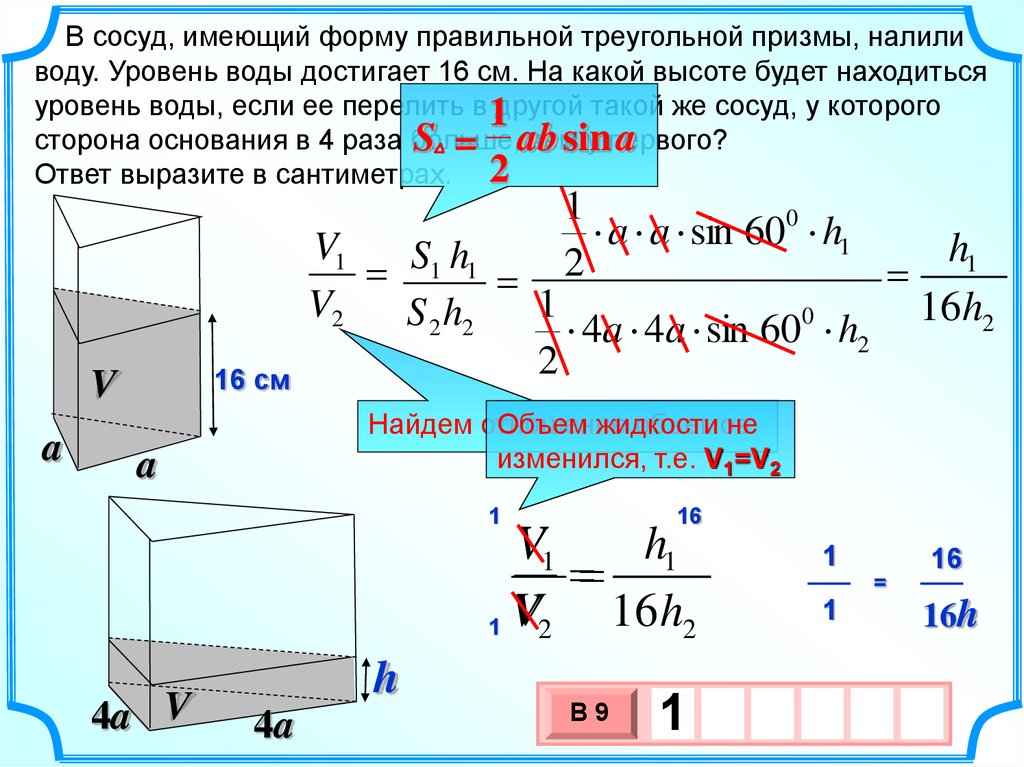
2) Используйте весы, чтобы найти массу объекта. Теперь, исходя из определения плотности, мы приходим к следующему уравнению, которое можно использовать для расчета плотности объекта:
Плотность = Масса ÷ Объем
Например, если расчетный объем объекта 4 мл. и его масса 8 гм, то его плотность будет (8 ÷ 4) = 2 г / мл
Таким образом, Архимед более 2000 лет назад придумал метод вытеснения воды, который можно было использовать для определения объема неправильного объекта.В то время изобретение этого метода было большим достижением, и благодаря своей простоте и высокой точности он остается актуальным и в наше время.
.2 * л
Введите значение во все поля
Вычислитель объема трубы Сечение трубы вычисляет объем трубы (V) на основе внутреннего диаметра (d) круглого канала или трубы и длины (l) трубы.
ИНСТРУКЦИИ: Выберите единицы и введите следующее:
- ( d ) Это внутренний диаметр трубы.
- ( л ) Это длина трубы.
Объем трубы (V): Калькулятор возвращает объем в галлонах. Однако их можно автоматически преобразовать в совместимые единицы с помощью раскрывающегося меню.
Сантехнические калькуляторы общего назначения
The Math / Science
Уравнение объема трубы:
, где:
- V = внутренний объем секции трубы
- d = внутренний диаметр
- л = длина трубы
Расширьте возможности vCalc с помощью бесплатной учетной записи
Зарегистрируйтесь сейчас!
Извините, JavaScript должен быть включен.
Измените параметры браузера и повторите попытку.
.
Расход жидкости из контейнеров
Отверстия в основании
Можно рассчитать скорость жидкости на выходе при сливе бака или контейнера
v = C v (2 г H) 1 / 2 (1a)
, где
v = выходная скорость (м / с)
C v = коэффициент скорости (вода 0,97)
g = ускорение свободного падения (9.
81 м / с 2 )
H = высота (м)
Объемный расход жидкости можно рассчитать
V = C d A (2 г H) 1/2 (1b)
, где
V = объемный расход (м 3 / с)
A = площадь отверстия — выходное отверстие (м 2 )
C d = коэффициент расхода
, где
C d = C c C v
, где
C c = коэффициент сжатия (апертура острого края 0.62, хорошо закругленное отверстие 0,97)
A = площадь отверстия (м 2 )
Пример — объемный расход при опорожнении контейнера
Высота от поверхности до выходного отверстия в резервуаре, заполненном водой, составляет 3 м . Проем с острой кромкой диаметром 0,1 м . Коэффициент расхода можно рассчитать как
C d = 0,62 0,97
= 0,6
Площадь отверстия может быть рассчитана как
A = π ((0.
1 м) / 2) 2
= 0,008 м 2
Объемный расход через отверстие можно рассчитать как
V = 0,6 (0,008 м 2 ) (2 (9,81 м / с 2 ) (3 м)) 1/2
= 0,037 м 3 / с
Для высоты 1,5 м объемный расход 0,1 м 3 / с . Для высоты 0,5 м объемный расход 0.06 м 3 / с .
Калькулятор сливного бака
Этот калькулятор основан на ур. (1b) и может использоваться для оценки объемного расхода , и , время , используемое для опорожнения контейнера или резервуара через отверстие.
Калькулятор делит контейнер на «фрагменты» и выполняет итеративное вычисление среднего значения для каждого фрагмента. Точность расчета можно повысить, увеличив количество срезов.
Площадь дна цистерны или контейнера (м 2 )
H — высота между поверхностью и проемом (м)
A — площадь проема (м 2 )
C d — коэффициент расхода
нет.
«срезов» (для итеративного расчета)
— результаты в таблице ниже!
Примечание! — поток уменьшается, а время увеличивается с уменьшением высоты.
Маленькие боковые отверстия
Выходная скорость может быть выражена как
v = C v (2 г H) 1/2 (2a)
Расстояние s может быть выражено как
s = 2 (H h) 1/2 (2b)
Объемный расход можно выразить как
V = C d A (2 г H) 1/2 (2c)
Сила реакции может быть выражена как
F = ρ V v (2d)
, где
ρ = плотность (кг / м 3 ) (вода 1000 кг / м 3 )
Большие боковые отверстия
Объемный расход можно выразить как
V = 2/3 C d b (2 г) 900 17 1/2 (H 2 3/2 — H 1 3/2 ) (3a)
, где
b = ширина проема (м)
Избыточное давление в контейнере
Скорость на выходе может быть выражена как
v = C v (2 (г H + p / ρ)) 1/2 (4a)
где
p = избыточное давление в контейнере или резервуаре (Н / м 2 , Па)
Объемный расход можно выразить как
V = C d A (2 (г H + р / р)) 1/2 (4б)
.
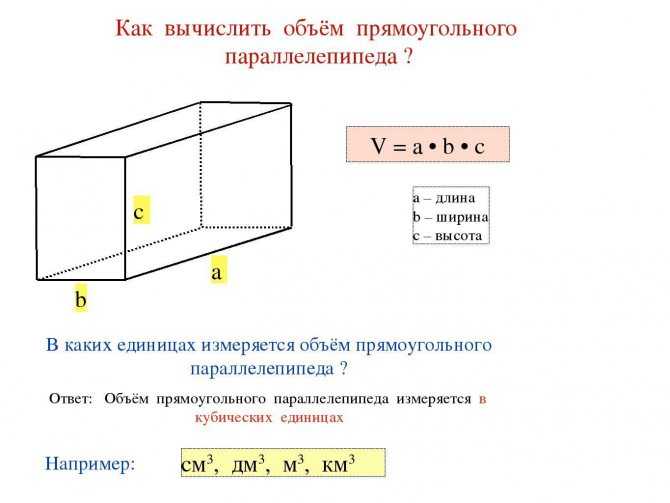
Формулы объема и площади поверхности многогранников: призма, пирамида, куб, параллелепипед
Изучение стереометрии начинается со знания формул. Для решения задач ЕГЭ по стереометрии нужны всего две вещи:
- Формулы объёма — например, объём куба, объём призмы, объем пирамиды — и формулы площади поверхности.
- Элементарная логика.
Все формулы объёма и формулы площади поверхности многогранников есть в нашей таблице.
| Куб | диагональ | |
| Параллелепипед | высота | |
| Прямоугольный параллелепипед | ||
| Призма | ||
| Пирамида |
Проще всего найти объём куба — это куб его стороны.
Вот, оказывается, откуда берётся выражение «возвести в куб».
Объём параллелепипеда тоже легко найти. Надо просто перемножить длину, ширину и высоту.
Объём призмы — это произведение площади её основания на высоту. Если в основании треугольник — находите площадь треугольника. Если квадрат — ищите площадь квадрата. Напомним, что высота — это перпендикуляр к основаниям призмы.
Объём пирамиды — это треть произведения площади основания на высоту. Высота пирамиды — это перпендикуляр, проведенный из её вершины к основанию.
Некоторые задачи по стереометрии решаются вообще без формул! Например, эта.
Задача 1.Объём куба равен . Найдите объём четырёхугольной пирамиды, основанием которой является грань куба, а вершиной — центр куба.
Решение:
Обойдёмся без формул! Просто посчитайте, сколько нужно таких четырёхугольных пирамидок, чтобы сложить из них этот куб 🙂
Очевидно, их 6, поскольку у куба 6 граней.
Стереометрия — это просто! Для начала выучите формулы объёма и площади поверхности многогранников и тел вращения.
А дальше — читайте о приемах решения задач по стереометрии.
Разберем задачи, где требуется найти площадь поверхности многогранника.
Мы рассмотрим призмы и пирамиды. Начнем с призмы.
Площадь полной поверхности призмы можно найти как сумму площадей всех ее граней. А это площади верхнего и нижнего оснований плюс площадь боковой поверхности.
Площадь боковой поверхности призмы – это сумма площадей боковых граней, которые являются прямоугольниками. Она равна периметру основания, умноженному на высоту призмы.
Задача 2. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Решение.
Многогранник на рисунке – это прямая призма с высотой 12.
Чтобы найти площадь основания, разделим его на два прямоугольника и найдем площадь каждого:
(больший квадрат), (маленький прямоугольник),
Подставим все данные в формулу: и найдем площадь поверхности многогранника:
Ответ: 424.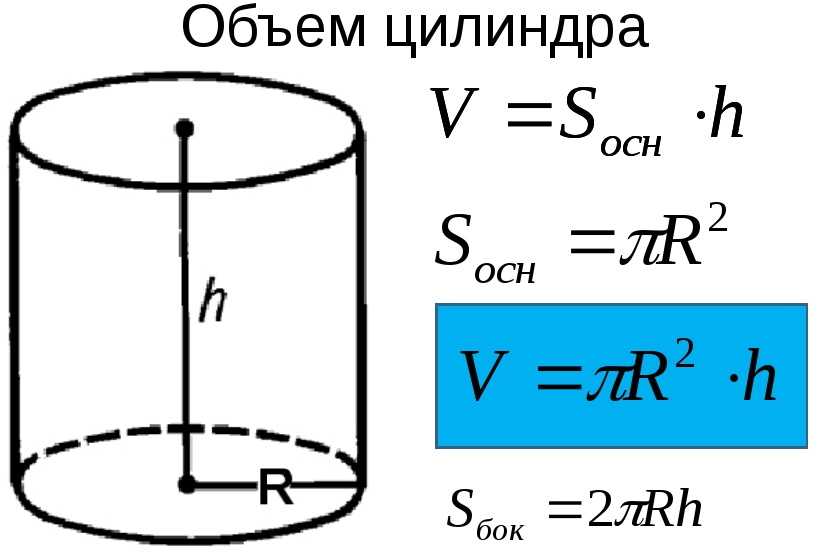
Задача 3. Найдите площадь поверхности многогранника, изображённого на рисунке (все двугранные углы прямые).
Решение.
Перевернем многогранник так, чтобы получилась прямая призма с высотой 1.
Площадь поверхности этой призмы находится по формуле:
Найдем площадь основания. Для этого разделим его на два прямоугольника и посчитаем площадь каждого:
(большой прямоугольник), (маленький прямоугольник).
Найдем площадь полной поверхности:
Ответ: 54
Задача 4.Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Решение.
Покажем еще один способ решения задачи.
Посмотрим, как получился такой многогранник. Можно сказать, что к «кирпичику», то есть прямоугольному параллелепипеду со сторонами 4, 1 и 3, сверху приклеен «кубик», все стороны которого равны 1.
И значит, площадь поверхности данного многогранника равна сумме площадей поверхностей прямоугольного параллелепипеда со сторонами 4,1,3 и
куба со стороной 1, без удвоенной площади квадрата со стороной 1:
Почему мы вычитаем удвоенную площадь квадрата? Представьте себе, что нам надо покрасить это объемное тело.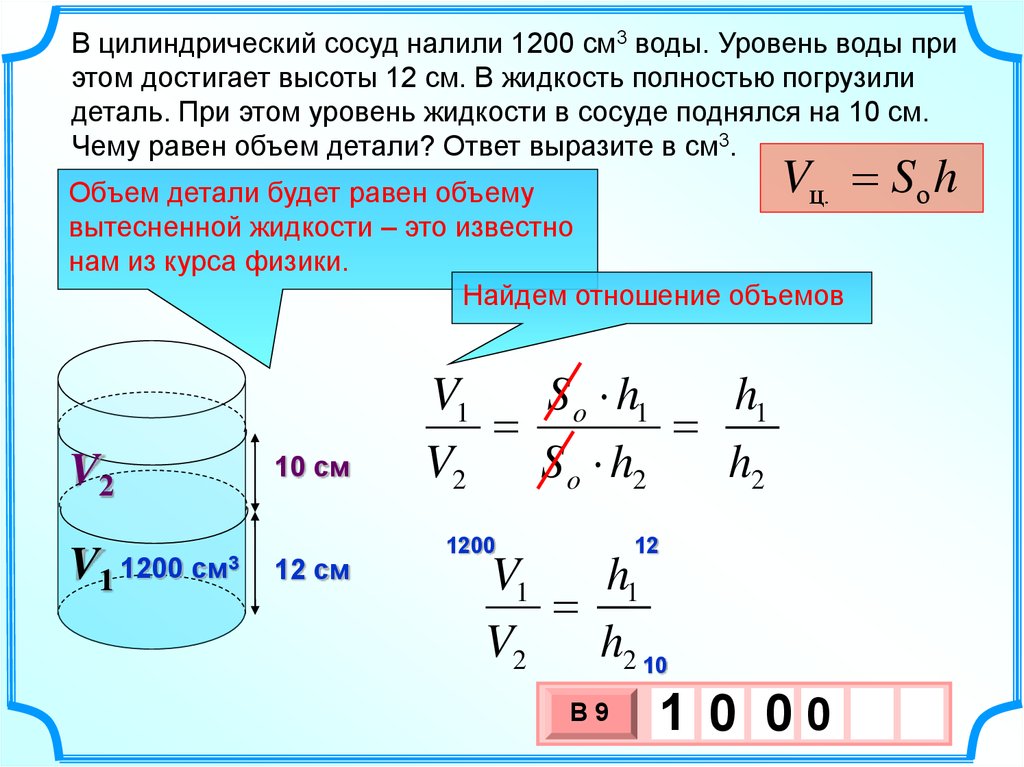
Мы красим все грани параллелепипеда, кроме квадрата на верхней его грани, где на него поставлен кубик. И у куба мы покрасим все грани, кроме этого квадрата.
Ответ: 42
Задача 5. . Основание прямой призмы – треугольник со сторонами 5 см и 3 см и углом 120° между ними. Наибольшая из площадей боковых граней равна 35 см². Найдите площадь боковой поверхности призмы.
Решение.
Пусть АВ = 5 см, ВС = 3 см, тогда
Из по теореме косинусов найдем ребро АС:
Отрезок АС – большая сторона , следовательно, большая боковая грань призмы.
Поэтому или откуда
Ответ: 75
Теперь две задачи на площадь боковой поверхности пирамиды.
Задача 6. Основанием пирамиды DАВС является треугольник АВС, у которого АВ = АС = 13, ВС = 10; ребро АD перпендикулярно к плоскости основания и равно 9. Найдите площадь боковой поверхности пирамиды.
Решение.
Площадь боковой поверхности пирамиды – это сумма площадей всех ее боковых граней.
Проведем , тогда (по теореме о 3-х перпендикулярах), то есть DК – высота треугольника DВС.
– равнобедренный (по условию АВ = АС), то высота АК, проведенная к основанию ВС, является и медианой, то есть ВК = КС = 5.
Из прямоугольного получим:
Из прямоугольного имеем:
(по двум катетам), тогда следовательно
Ответ: 192
Задача 8. Стороны основания правильной четырехугольной пирамиды равны 24, боковые ребра равны 37. Найдите площадь поверхности пирамиды.
Решение:
Так как четырехугольная пирамида правильная, то в основании лежит квадрат, а все боковые грани — равные равнобедренные треугольники.
Площадь поверхности пирамиды равна
где р – полупериметр основания, h — апофема (высота боковой грани правильной пирамиды), a – сторона основания.
Значит, полупериметр основания .
Апофему найдем по теореме Пифагора:
Ответ: 2256
Как решать задачи на нахождение объема многогранника сложной формы?
Покажем два способа.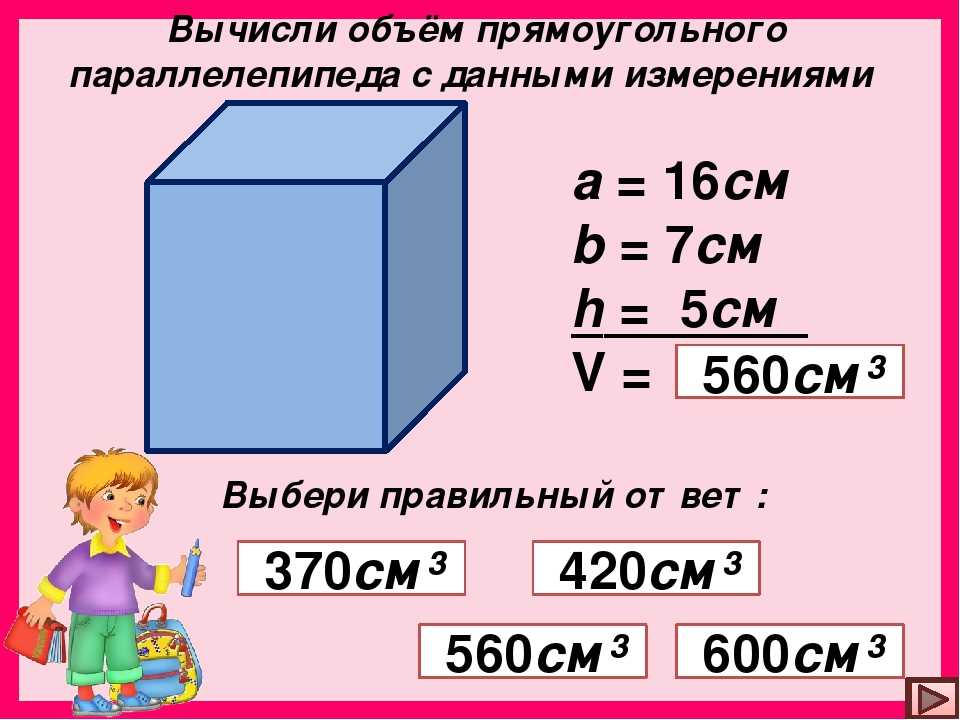
Первый способ
1.Составной многогранник достроить до полного параллелепипеда или куба.
2.Найти объем параллелепипеда.
3.Найти объем лишней части фигуры.
4.Вычесть из объема параллелепипеда объем лишней части.
Второй способ.
1.Разделить составной многогранник на несколько параллелепипедов.
2.Найти объем каждого параллелепипеда.
3.Сложить объемы.
Задача 9. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Решение.
1) Достроим составной многогранник до параллелепипеда.
2) Найдем объем параллелепипеда – для этого перемножим его длину, ширину и высоту:
3) Найдем объем лишней части, то есть маленького параллелепипеда.
Его длина равна 9 – 4 = 5, ширина 4, высота 7, тогда его объем
4) Вычтем из объема параллелепипеда объем лишней части и получим объем заданной фигуры:
Ответ: 220.
Задача 10.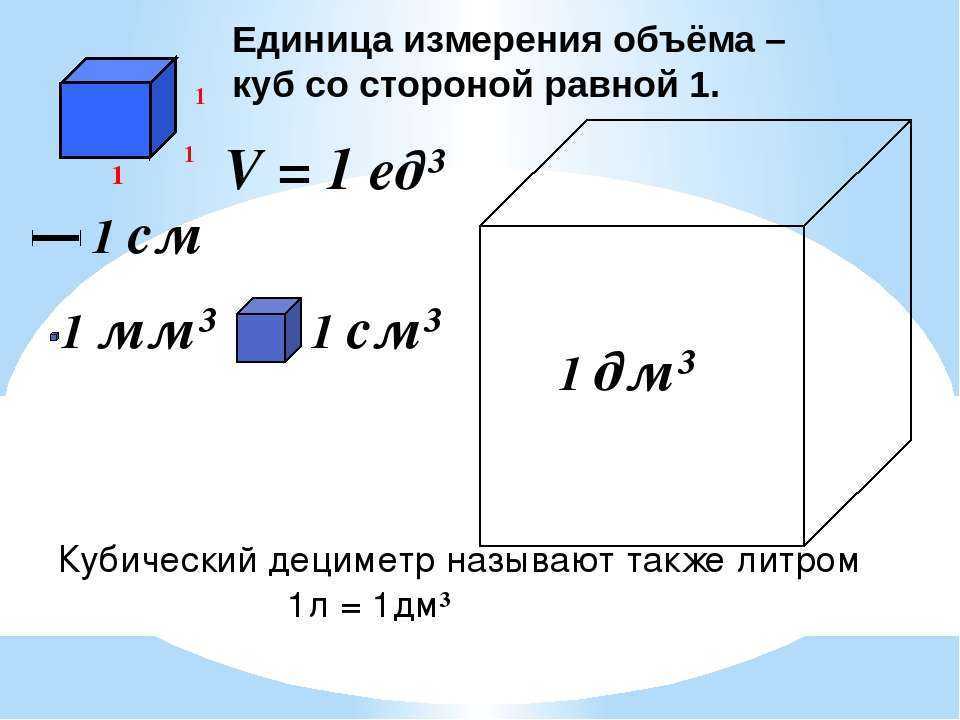
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 7, боковое ребро равно 6. Найдите объем призмы.
Объем призмы равен , а так как призма прямая, то ее боковое ребро является и высотой, то есть
Основанием призмы является прямоугольный треугольник c катетами 6 и 7, тогда площадь основания
Ответ: 126
Задача 11. В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 324 см. На какой высоте будет находиться уровень воды, если ее перелить в другой сосуд, у которого сторона в 9 раз больше, чем у первого? Ответ выразите в сантиметрах.
Решение.
Объем призмы равен
Воду перелили в другой такой же сосуд. Это значит, что другой сосуд также имеет форму правильной треугольной призмы, но все стороны основания второго сосуда в 9 раз больше, чем у первого.
Основанием второго сосуда также является правильный треугольник. Он подобен правильному треугольнику в основании первого сосуда.
Отношение площадей подобных фигур равно квадрату коэффициента подобия.
Если все стороны треугольника увеличить в 9 раз, его площадь увеличится в раз. Мы получили, что площадь основания второго сосуда в 81 раз больше, чем у первого.
Объем воды не изменился, Так как высота воды должна быть в 81 раз меньше, чем Она равна (см).
Ответ: 4
Задача 12. Объем параллелепипеда Найдите объем треугольной пирамиды
Решение.
Опустим из вершины высоту Н на основание
Диагональ основания делит его на два равных треугольника, следовательно,
Имеем:
Ответ: 3,5
Задача 13. Найдите объем правильной треугольной пирамиды, стороны основания которой равны 8, а высота равна
Решение.
По формуле объема пирамиды, .
В основании пирамиды лежит правильный треугольник. Его площадь равна
Объем пирамиды
Ответ: 96
Задача 14. Через середины сторон двух соседних ребер основания правильной четырехугольной призмы проведена плоскость, параллельная боковому ребру.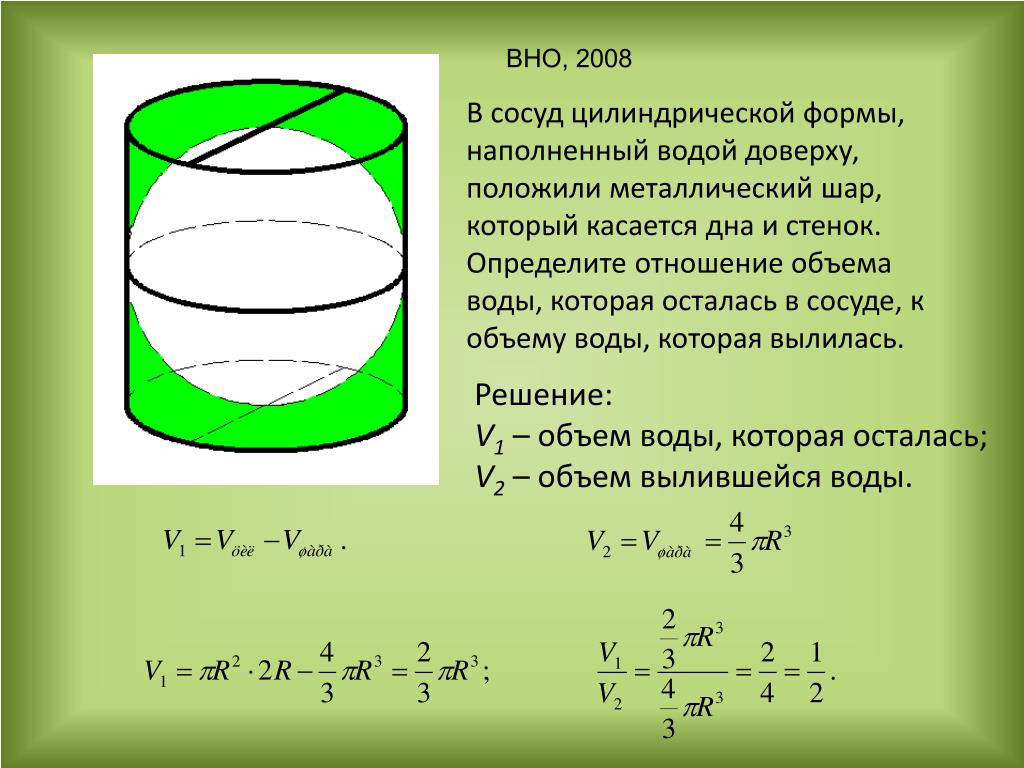
Найдите объем меньшей из частей, на которые эта плоскость делит призму, если объем призмы равен 32.
Решение.
По условию, призма правильная, значит, в ее основании лежит квадрат, а высота равна боковому ребру.
Пусть тогда
Так как точки М и К – середины АD и DС соответственно, то
Площадь треугольника MDK, лежащего в основании новой призмы, составляет часть площади квадрата в основании исходной призмы.
Высоты обеих призм одинаковые. Согласно формуле объема призмы: , и значит, объем маленькой призмы в 8 раз меньше объема большой призмы. Он равен
Ответ: 4
Докажем полезную теорему.
Теорема: Площадь боковой поверхности наклонной призмы равна произведению периметра перпендикулярного сечения на боковое ребро.
Доказательство:
Плоскость перпендикулярного сечения призмы перпендикулярна к боковым ребрам, поэтому стороны перпендикулярного сечения призмы являются высотами параллелограммов.
Больше задач на формулы объема и площади поверхности здесь.
Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Формулы объёма и площади поверхности. Многогранники.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
07.01.2023
Нахождение объема колбы. Студент получил чистую сухую колбу с пробкой. Она взвесила колбу и пробку на аналитических весах и обнаружила, что общая масса составляет 34,166 г. Затем она наполнила колбу водой и получила массу для полной закупоренной колбы 68,090 г. По этим данным, а также по тому, что при температуре лаборатории плотность воды была 0,9975 г/мл, найдите объем закрытой пробкой колбы.
а. Сначала нам нужно получить массу воды в колбе. Это находят, признавая, что масса образца равна сумме масс его частей. Для наполненной закупоренной колбы: Масса наполненной закупоренной колбы = масса пустой закупоренной колбы + масса воды, поэтому масса воды = масса наполненной колбы − масса пустой колбы Масса воды = _ _ _ _ _ g − _ _ _ _ _ g = _ _ _ _ _ _ g Многие измерения массы и объема в химии производятся методом, используемым в 1а. Этот метод называется измерением по разнице, и он очень полезен. б. Плотность чистого вещества равна его массе, деленной на его объем: Плотность = масса объема или объем = массовая плотность Объем колбы равен объему содержащейся в ней воды. Зная массу и плотность воды, мы можем найти ее объем и объем колбы. Произведите необходимый расчет. Объем воды = объем колбы = _ _ _ _ _ _ _ мл
Глава 1, Задача 1ASA
Нахождение объема колбы.
Студент получил чистую сухую колбу с пробкой. Она взвесила колбу и пробку на аналитических весах и обнаружила, что общая масса
34.
166
грамм
. Затем она наполнила колбу водой и получила массу для полной закупоренной колбы.
68.090
грамм
. Из этих данных, а также из того, что при температуре лаборатории плотность воды была
0,9975
грамм
/
мл
, найдите объем закупоренной колбы.
а. Сначала нам нужно получить массу воды в колбе. Это находят, признавая, что масса образца равна сумме масс его частей. Для наполненной, закупоренной колбы:
Масса наполненной закупоренной колбы
знак равно
масса пустой закрытой колбы
+
масса воды
,
такая масса воды
знак равно
масса наполненной колбы
−
масса пустой колбы
масса
из
воды
знак равно
_
_
_
_
_
грамм
−
_
_
_
_
_
грамм
знак равно
_
_
_
_
_
_
грамм
Многие измерения массы и объема в химии производятся методом, используемым в 1а.
Этот метод называется измерением по разнице, и он очень полезен.
б. Плотность чистого вещества равна его массе, деленной на его объем:
Плотность
знак равно
масса
объем
или
объем
знак равно
масса
плотность
Объем колбы равен объему содержащейся в ней воды. Зная массу и плотность воды, мы можем найти ее объем и объем колбы. Произведите необходимый расчет.
Объем
из
воды
знак равно
объем колбы
знак равно
_
_
_
_
_
_
_
мл
Расшифровка:
Подсчитывается объем закупоренной колбы, содержащей воду плотностью 0,9975 г/мл.
Введение понятия:
Деление массы вещества на его объем называется плотностью этого вещества. Выражение, которое используется для обозначения плотности любого вещества, приведено ниже.
Плотность=масса-объем
Единицей плотности в системе СИ является г/мл.
Объем закупоренной колбы, содержащей воду плотностью 0,9975 г/мл составляет 34,009 мл.
Указанная общая масса пустой фляги с пробкой составляет 34,166 г.
Наблюдаемая масса закупоренной колбы, наполненной водой, составляет 68,090 г.
Плотность воды 0,9975 г/мл.
Масса воды
Во-первых, необходимо рассчитать массу воды, находящейся в закупоренной колбе.
Массу наполненной закупоренной колбы рассчитывают по выражению, приведенному ниже.
Масса наполненной колбы с пробкой = масса пустой колбы с пробкой + масса воды
Приведенное выше выражение изменено для расчета массы воды, находящейся в закрытой пробкой колбе, как указано ниже.
Масса воды = масса наполненной колбы – масса пустой колбы
Подставьте значения пустой и наполненной колбы в приведенное выше выражение.
Масса воды=68,090 г−34,166 г=33,924 г
Таким образом, масса воды составляет 33,924 г.
Плотность любого вещества рассчитывается по приведенному ниже выражению.
Плотность=массобъем
Приведенное выше выражение изменено для расчета объема воды, находящегося в закрытой пробкой колбе, как указано ниже.
Объем=плотность массы
Подставьте значения массы и плотности воды в приведенное выше выражение.
Объем=33,924 г 0,9975 г/мл=34,009 мл
Итак, объем воды равен 34,009 мл.
Поскольку объем колбы равен объему находящейся в ней воды, следовательно, объем закупоренной колбы также равен 34,009мл.
Объем закупоренной колбы, содержащей воду, составляет 34,009 мл.
Хотите увидеть больше полных решений, подобных этому?
Подпишитесь сейчас, чтобы получить доступ к пошаговым решениям миллионов задач из учебников, написанных экспертами в данной области!
chevron_right
Next chevron_right
Глава 1, задача 2ASA
Было обнаружено, что тонкий лист никеля размером 5,00 см на 7,00 см весит 0,350 г.
2 в течение 14 дней подряд. BSA пациента размером 5 футов и 1 дюйм в высоту и весом 92, а общее количество, введенное за 2-недельный период, составляет ____ г.
Калькулятор объема воды в бассейне — PSG
Основы расчета объема бассейна
Чтобы измерить объем вашего бассейна, вам понадобится несколько основных элементов уравнения.
A: Область
L: Длина
W: Ширина
D: Глубина
H: Высота
V: Том
R: Radius
D: .0006 Диаметр
Pi: 3,14 константа
Как рассчитать объем
Вычислил кубический объем, включив площадь поверхности и глубину бассейна. Для точных расчетов бассейн следует разделить на различные зоны по глубине.
Бассейны постоянной глубины: квадратные или прямоугольные
Длина x ширина x средняя глубина = объем (в кубических метрах)
Длина, умноженная на ширину, дает площадь поверхности бассейна.
Умножение на глубину дает объем в кубических метрах.
Бассейны переменной глубины: квадратные или прямоугольные
Длина x ширина x средняя глубина = объем (в кубических метрах)
Длина, умноженная на ширину, дает площадь поверхности бассейна. Умножение этого значения на среднюю глубину дает объем в кубических метрах.
Измерьте длину, ширину и среднюю глубину бассейна, округлив каждое измерение до ближайшего метра.
Если мелкая часть составляет 0,5 м, а глубокая — 1 м, а наклон дна бассейна плавный и ровный, то средняя глубина составляет 0,75 м
- Средняя глубина = (Глубина на мелководье + Глубина на глубоком конце) / 2
- Средняя глубина = ( 0,5 + 1 ) / 2 = 0,75 м
Если большая часть бассейна мелкая, а затем внезапно обрывается до глубокого конца, у вас будет другая средняя глубина. В таком случае вы можете рассматривать пул как две части. Измерьте длину, ширину и среднюю глубину неглубокой секции, затем выполните те же измерения для более глубокой секции.
Рассчитайте объем неглубокой части и добавьте его к объему, рассчитанному для более глубокой части.
Обязательно используйте в своих расчетах реальную глубину воды, а не глубину контейнера. Расчет точного объема имеет решающее значение, так как это может привести к серьезным ошибкам при добавлении химикатов, которые добавляются в зависимости от объема воды.
Формула: π х радиус в квадрате х средняя глубина = объем
Число 3,14 относится к числу пи, которое является математической константой. Радиус равен половине диаметра, поэтому измерьте расстояние по самой широкой части круга и разделите его на 2, чтобы найти радиус. Квадрат означает, что число умножается само на себя, поэтому умножьте радиус на себя.
Например, если диаметр равен 3 м, мы можем уменьшить это значение вдвое для радиуса 1,5 м. Теперь, чтобы найти радиус в квадрате, умножьте 1,5 м на само по себе, чтобы получить 2,25 м 2 .
Имея эту информацию, вы можете вернуться к формуле:
π x радиус в квадрате x средняя глубина = объем
3,14 x 2,25 м в квадрате x 0,75 м = 150 м вам может потребоваться рассчитать две или три секции внутри джакузи и сложить их вместе, чтобы получить общий объем из-за сидений.