Квантовая жидкость и сверхтекучесть. Сверхтекучесть воды
Как правильно плавать в сверхтекучей жидкости / Geektimes
Как мы знаем, любое плывущее в жидкости тело рано или поздно остановится за счет сил вязкого трения, если его движение не поддерживается каким-нибудь двигателем. Но есть жидкости, называемые сверхтекучими, в которых вязкое трение отсутствует(*). Самый известный пример сверхтекучей жидкости – это жидкий гелий, охлажденный, как минимум, до 2.17 градусов выше абсолютного нуля температуры.Движение при полном отсутствии вязкости проявляется во многих впечатляющих эффектах: сверхтекучий гелий легко протекает через самые узкие щели и трещины, способен бесконечно течь по кругу(**) и вытекать из сосуда через тончайшую жидкую пленку, налипшую на его стенки. Все эти явления – примеры крупномасштабных квантовых эффектов.
В недавней теоретической статье был рассмотрен вопрос: можно ли плавать в сверхтекучей жидкости? Иными словами, может ли гипотетический пловец, двигая руками и ногами, создавать силу тяги, позволяющую ему разгоняться или замедляться, не задействуя силы вязкого трения?
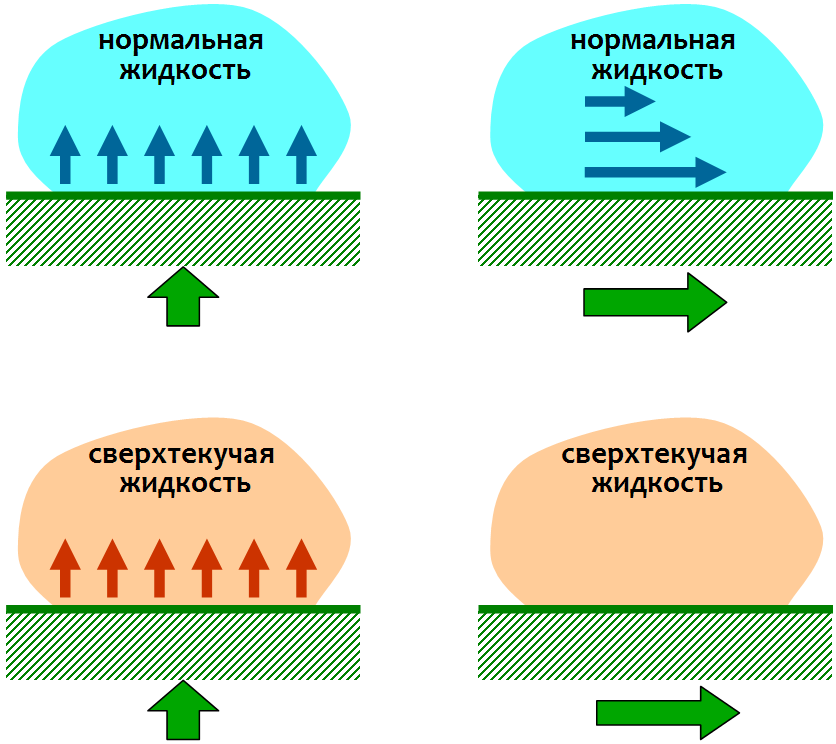
Осознать нетривиальность ответа на этот вопрос можно, рассматривая поведение нормальной и сверхтекучей жидкостей при взаимодействии с телами. Как показано на рисунке, нормальную жидкость можно заставить двигаться, как толкая ее поверхностью твердого тела, так и увлекая ее за собой за счет сил вязкого трения. В сверхтекучей жидкости последнее не получится: трение в ней отсутствует, и ее можно только толкать, что, как мы увидим, делает невозможным некоторые способы плавания.
Для анализа общих принципов физических явлений принято рассматривать простые модели «сферических коней в вакууме». Обсуждаемая статья не является исключением: в ней были рассмотрены двухтельный и трехтельный модельные «пловцы», представляющие собой два и три эллипсоида, соединенных «суставами». Пловцы могут двигать своими эллипсоидами, сгибая и разгибая суставы. Если у пловца получится отталкиваться от окружающей жидкости, он создаст силу тяги и начнет двигаться.
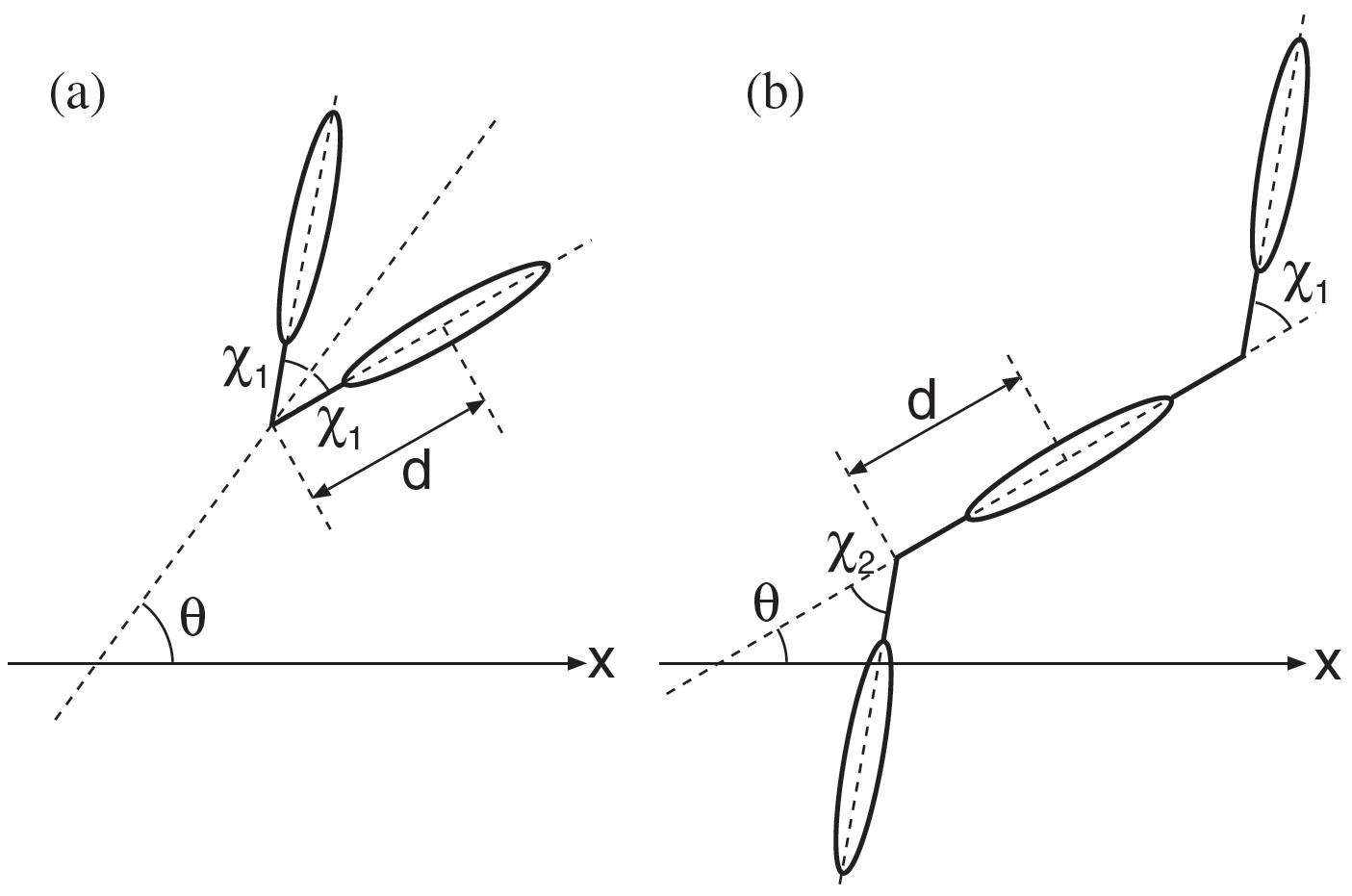
Двухтельный пловец похож на двустворчатого моллюска и может пытаться плыть, периодически изменяя угол между своими эллипсоидами подобно машущей крыльями бабочке. Однако расчеты показывают, что плыть у него не получится: при взмахах пловец перемещается вперед и назад, но в среднем остается на месте (здесь можно посмотреть видео его незамысловатых движений).
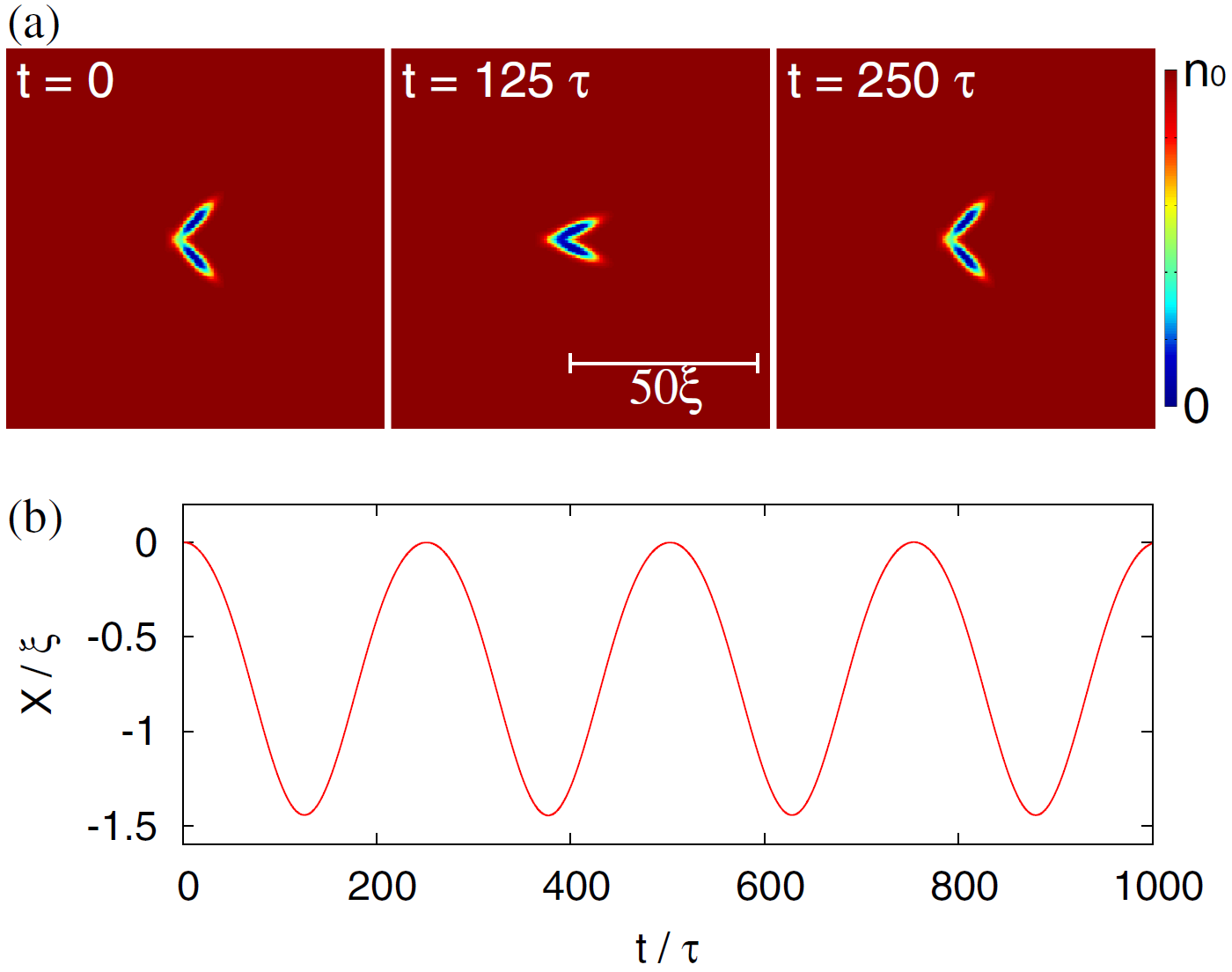 Наверху: профиль плотности сверхтекучей жидкости в разные моменты времени. Синие участки, откуда жидкость выталкивается – это эллипсоиды двухтельного пловца. Внизу: координата пловца как функция времени.
Наверху: профиль плотности сверхтекучей жидкости в разные моменты времени. Синие участки, откуда жидкость выталкивается – это эллипсоиды двухтельного пловца. Внизу: координата пловца как функция времени.Можно провести параллели между этим результатам и теоремой Пёрселла о морском гребешке (Purcell’s scallop theorem). Эта важная теорема теории плавания гласит, что двустворчатый моллюск, медленно открывающий и закрывающий свою раковину в вязкой жидкости, не будет никуда плыть, коль скоро его движения будут обратимы во времени. Последнее означает, что периодические открывания и закрывания створок раковины не меняют свой вид при запуске времени в обратном направлении (можно представить себе видеоролик, выглядящий просмотре задом наперед точно так же, как при нормальном воспроизведении). В нашем случае жидкость не имеет вязкости, и работает не сама теорема Пёрселла, а ее аналог для сверхтекучей жидкости.
 Рисунок из доклада Эдварда Пёрселла (лауреата Нобелевской премии по физике в 1952 году).
Рисунок из доклада Эдварда Пёрселла (лауреата Нобелевской премии по физике в 1952 году).Ситуация меняется, когда двухтельный пловец начинает размахивать своими эллипсоидами с большей частотой. Если скорость их движения превышает скорость звука в жидкости, начинают испускаться звуковые волны и вихри(***). Эти возбуждения уносят с собой некоторый импульс, который, за счет отдачи, заставляет пловца двигаться. На рисунке видно, что в этом случае его координата хоть и колеблется, но с течением времени в целом уменьшается, а это значит, что пловец движется справа налево. После десяти колебаний (справа от пунктирной линии на графике) взмахи створками прекращаются, и пловец продолжает двигаться по инерции (видео).
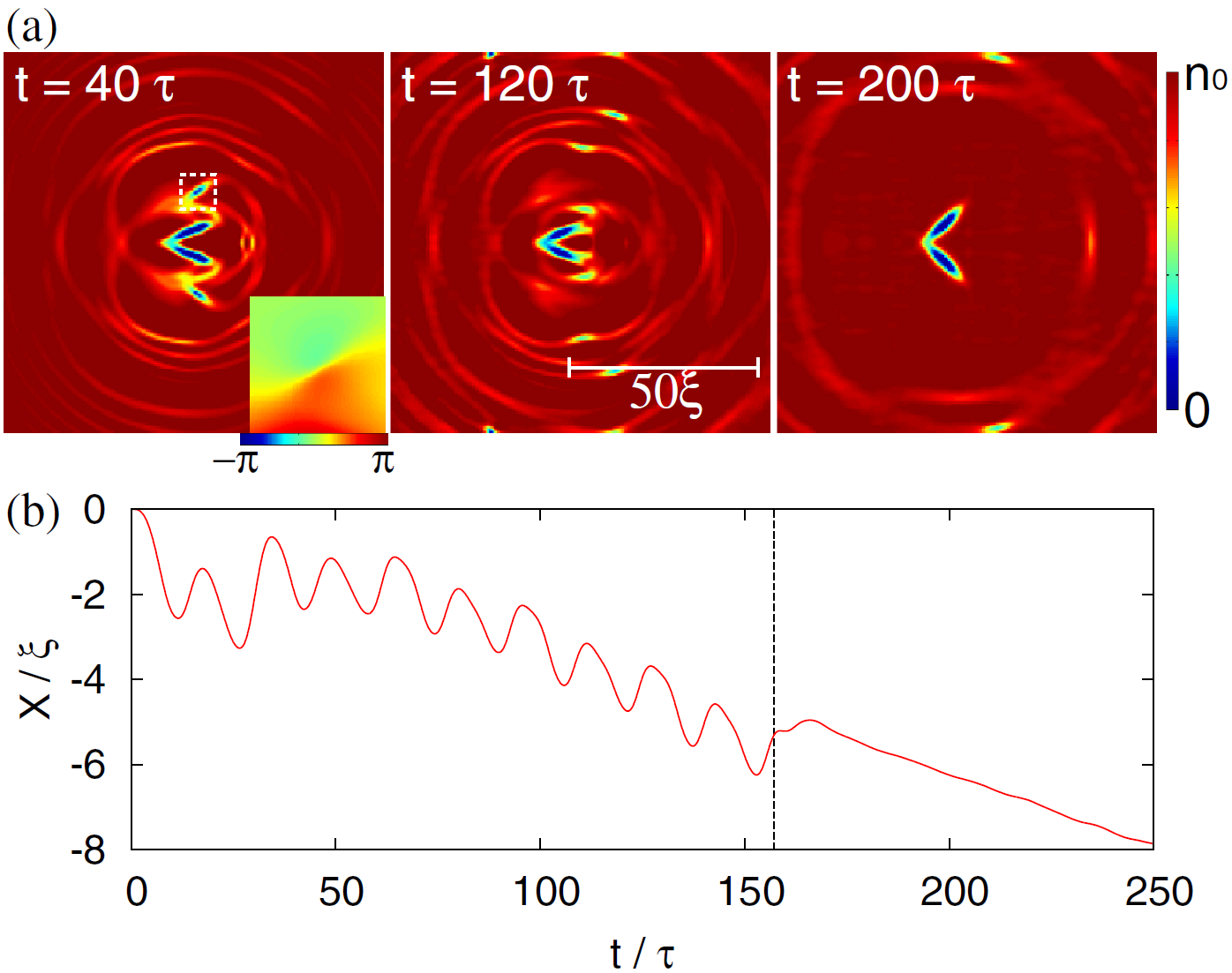
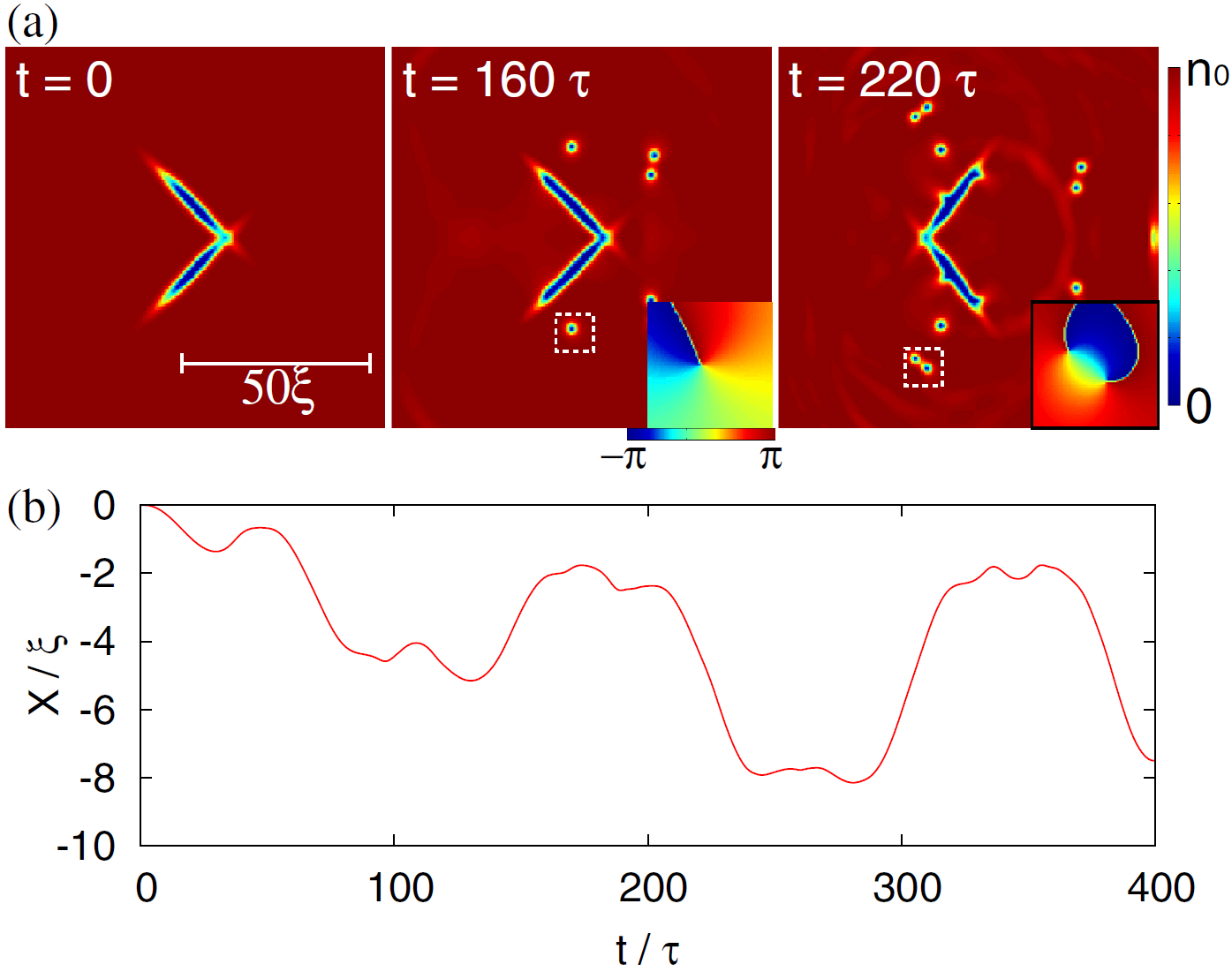
Можно попробовать и другой тип движения пловца, когда его створки смыкаются и раздвигаются не только в правом направлении, а попеременно в двух направлениях. Такие симметричные движения похожи на взмахи крыльев бабочки. Расчеты показывают, что при этом возбуждается много квантованных вихрей (они видны на рисунке как маленькие кружочки), но, в целом, плавание не очень эффективно. Причина в том, что возбуждается примерно одинаковое количество вихрей, движущихся как вправо, так и влево, и уносимые ими импульсы в значительной мере компенсируют друг друга (видео).
Рассмотрим теперь трехтельного пловца. Перед двухтельным у него есть важное преимущество: он может извиваться, совершая змеевидные движения, которые не переходят сами в себя при обращении времени. А значит, теорема Пёрселла к нему неприменима, и он должен плыть даже при медленных движениях. Приведенные на рисунке расчеты подтверждают эту догадку: при извивающихся движениях пловец уверенно продвигается по горизонтали, при этом немного смещаясь и по вертикали (видео).
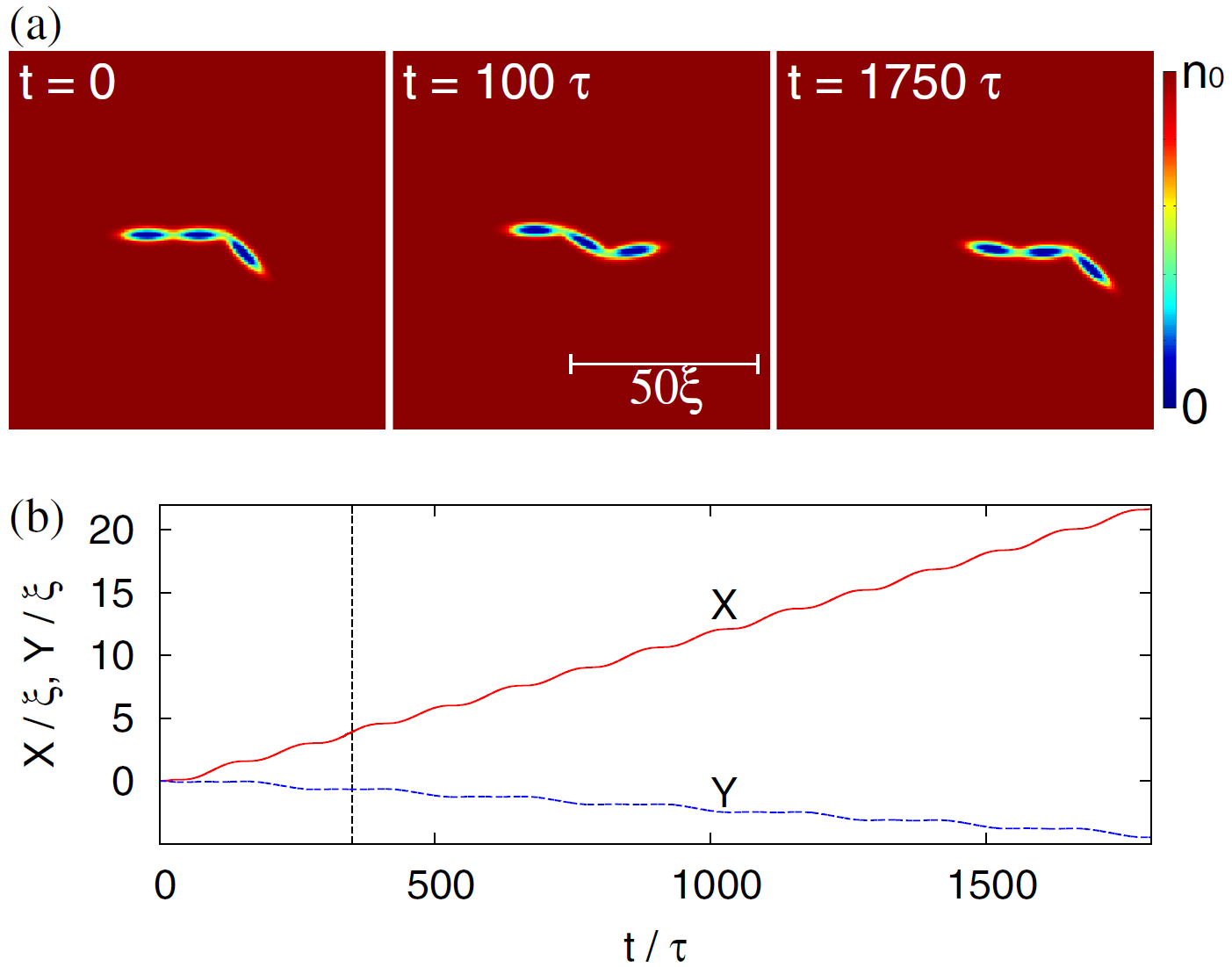 Наверху: профиль плотности сверхтекучей жидкости в разные моменты времени. Синие участки, откуда жидкость выталкивается – это эллипсоиды трехтельного пловца. Внизу: горизонтальная (X) и вертикальная (Y) координаты пловца как функции времени.
Наверху: профиль плотности сверхтекучей жидкости в разные моменты времени. Синие участки, откуда жидкость выталкивается – это эллипсоиды трехтельного пловца. Внизу: горизонтальная (X) и вертикальная (Y) координаты пловца как функции времени.Какое применение можно найти полученным результатам? Казалось бы, задача о плавании в сверхтекучей жидкости не особо актуальна на практике, но есть одна область, где она может быть полезной. В последнее время активно развиваются эксперименты с бозе-конденсацией и сверхтекучестью ультрахолодных атомных газов, с которыми связывают большие планы по созданию квантовых симуляторов, квантовых компьютеров и экспериментальному моделированию экзотических состояний материи. В таких системах можно создавать сгустки сверхтекучего газа одного вида, погруженные в сверхтекучий газ другого вида. Если мы сможем деформировать сгусток так, как нам нужно (а это можно делать с помощью лазерных лучей), то можно будет заставить этот сгусток плыть, отталкиваясь от окружающего газа. На рисунке показаны расчеты, демонстрирующие такую возможность: когда изменения формы сгустка не являются обратимыми во времени, ему действительно удается двигаться (видео).
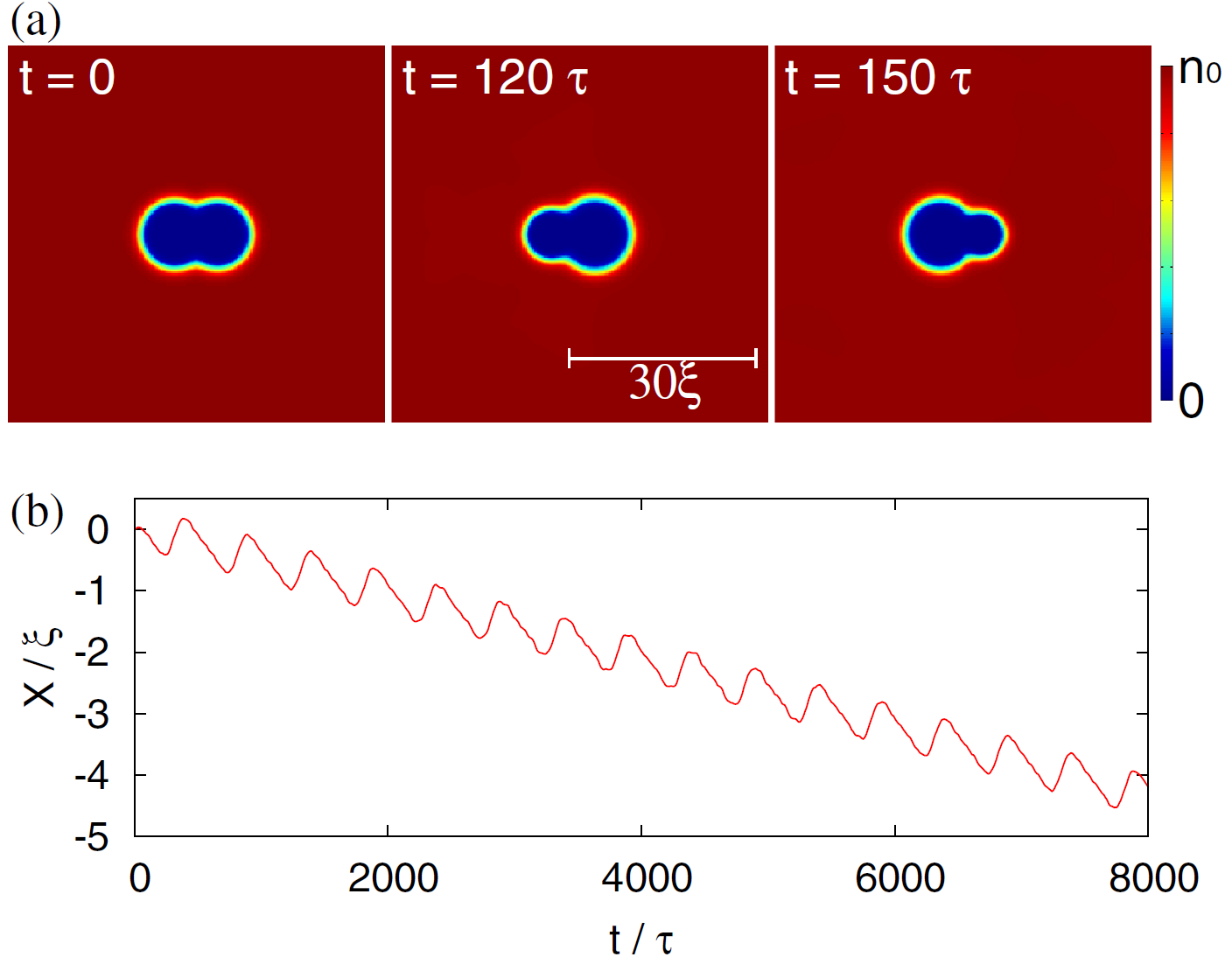
Итак, мы видим, что плавать в сверхтекучей жидкости нужно с умом: теорема Пёрселла гарантирует, что мы не сможем плыть, если наши движения руками и ногами будут совпадать с самими собой при проигрывании в обратном направлении. Чтобы начать перемещаться, нам нужно будет либо двигаться быстрее звука (что проблематично), либо извиваться подобно змее, нарушив обратимость движений во времени. Эти выводы хорошо знакомы плавающим в вязкой жидкости микроорганизмам: для того, чтобы обойти теорему Пёрселла, им приходится использовать спирально вращающиеся жгутики, являющиеся аналогами рассмотренного здесь трехтельного пловца.
По материалам статьи: Hiroki Saito, Can We Swim in Superfluids?: Numerical Demonstration of Self-Propulsion in a Bose–Einstein Condensate, Journal of the Physical Society of Japan 84, 114001 (2015).
(*)На самом деле, это не совсем так: любая реальная сверхтекучая жидкость может быть представлена как совокупность «нормальной» и сверхтекучей компонент (двухжидкостная модель), и нормальная компонента будет по-прежнему замедлять движущееся тело. Однако это не мешает сверхтекучей компоненте двигаться полностью без трения.
(**)На практике круговой поток сверхтекучего гелия может затухать, но не из-за вязкости, а за счет квантовомеханического процесса – проскальзывания квантованных вихрей. В экспериментах не наблюдалось никакого заметного затухания в течение 18 часов.
(***)Возникающие в сверхтекучей жидкости вихри – это не просто вихри наподобие маленьких торнадо, а квантованные топологические возбуждения. В отличие от обычных вихрей, они не могут просто исчезнуть за счет постепенного затухания потока.
geektimes.com
Сверхтекучая жидкость - это... Что такое Сверхтекучая жидкость?

Аномальное течение Гелия-II
Сверхтеку́честь — термодинамическая фаза квантовой жидкости, при котором она протекает через узкие щели и капилляры без трения. До недавнего времени сверхтекучесть была известна только у жидкого гелия, однако в последние годы сверхтекучесть была обнаружена и в других системах: в разреженных атомных бозе-конденсатах, твёрдом гелии.
Сверхтекучесть объясняется следующим образом. Поскольку атомы гелия являются бозонами, квантовая механика допускает нахождение в одном состоянии произвольного числа частиц. Вблизи абсолютного нуля температур все атомы гелия оказываются в наинизшем энергетическом состоянии. Поскольку энергия состояний дискретна, атом может получить не любую энергию, а только такую, которая равна энергетическому зазору между соседними уровнями энергии. Но при низкой температуре энергия столкновений может оказаться меньше этой величины, в результате чего рассеяния энергии попросту не будет происходить. Жидкость будет течь без трения.
Сверхтекучесть в жидком гелии
Основные факты
Сверхтекучесть жидкого гелия-II ниже лямбда-точки (T = 2,172 К) была открыта в 1938 году П. Л. Капицей (Нобелевская премия по физике за 1978 год). Уже до этого было известно, что при прохождении этой точки жидкий гелий испытывает фазовый переход, переходя из полностью «нормального» состояния (называемого гелий-I) в новое состояние так называемого гелия-II, однако только Капица показал, что гелий-II течёт вообще (в пределах экспериментальных погрешностей) без трения. На сегодняшний день установлено, что коэффициент вязкости у гелия-II меньше 10-12 Па·с, в то время как у гелия-I вблизи температуры 4,22 К этот коэффициент имеет величину порядка 10-6 Па·с.
Теория сверхтекучего гелия-II была разработана Л. Д. Ландау (Нобелевская премия по физике за 1962 год).
Двухжидкостная модель гелия-II

Рис.1 Относительная доля нормальной компоненты в гелии-II
В рамках двухжидкостной модели, гелий-II представляет собой смесь двух взаимопроникающих жидкостей: сверхтекучей и нормальной компонент. Сверхтекучая компонента представляет собой собственно жидкий гелий, находящийся в квантово-коррелированном состоянии, аналогичном состоянию бозе-конденсата (однако, в отличие от конденсата разреженных паров атомов, гелий находится в режиме сильной связи). Эта компонента движется без трения, обладает нулевой температурой и не участвует в переносе энергии в форме теплоты. Нормальная компонента представляет собой газ квазичастиц двух типов: фононов и ротонов, т. е. элементарных возбуждений квантовокоррелированной жидкости; она движется с трением и участвует в переносе энергии.
При нулевой температуре в гелии отсутствует свободная энергия, которую можно было бы потратить на рождение квазичастиц, и поэтому гелий находится полностью в сверхтекучем состоянии. При повышении температуры плотность газа квазичастиц (прежде всего, фононов) растёт, и доля сверхтекучей компоненты падает. Вблизи температуры лямбда-точки концентрация квазичастиц становится столь велика, что они образуют уже не газ, а жидкость квазичастиц, и наконец при превышении температуры лямбда-точки макроскопическая квантовая когерентность теряется, и сверхтекучая компонента пропадает вовсе. Относительная доля нормальной компоненты показана на Рис.1.
При протекании гелия сквозь щели с малой скоростью, сверхтекучая компонента, по определению, обтекает все препятствия без потери кинетической энергии, т. е. без трения. Трение могло бы возникнуть, если бы какой-либо выступ щели порождал бы квазичастицы, уносящие в разные стороны импульс жидкости. Однако такое явление при малых скоростях течения энергетически невыгодно, и только при превышении критической скорости течения начинают генерироваться ротоны.
Эта модель, во-первых, хорошо объясняет разнообразные термомеханические, светомеханические и т. п. явления, наблюдающиеся в гелии-II, а во-вторых, прочно базируется на квантовой механике.
Сверхтекучесть в иных системах
- В 1995 году в экспериментах с разреженными газами щелочных металлов были достигнуты достаточно низкие температуры для того, чтобы газ перешел в состояние бозе-эйнштейновского конденсата. Как и ожидалось на основании теоретических вычислений, полученный конденсат вёл себя как сверхтекучая жидкость. В последующих экспериментах было установлено, что при движении тел сквозь этот конденсат со скоростями меньше критической никакой передачи энергии от тела к конденсату не происходит.
- В 2004 году было объявлено об открытии сверхтекучести и у твёрдого гелия. Последующие исследования, однако, показали, что ситуация далеко не столь проста, и потому говорить об экспериментальном обнаружении этого явления пока преждевременно.
- С 2004 года, на основании результатов ряда теоретических работ[1] предполагается, что при давлениях порядка 4 миллионов атмосфер и выше водород становится не способным переходить в твердую фазу при любом охлаждении (как и гелий при нормальном давлении) образуя тем самым сверхтекучую жидкость. Прямые экспериментальные подтверждения или опровержения пока отсутствуют.
- В 2005 году была открыта сверхтекучесть в холодном разреженном газе фермионов [2].
- В 2009 году была продемонстрирована сверхтекучесть типа "supersolid" в холодном разреженном газе рубидия [3].
Современные направления исследования
- Турбулентность в сверхтекучей жидкости
- Сверхтекучесть в системах с внутренними степенями свободы
- Связь сверхпроводящих и сверхтекучих фаз
- Спиновая сверхтекучесть
- Поиск новых веществ со сверхтекучими фазами
Ссылки
Обзорные статьи
Wikimedia Foundation. 2010.
dic.academic.ru
Квантовая жидкость и сверхтекучесть

Сверхтекучесть гелия
Природа квантовой жидкости
Вещество переходит в состояние квантовой жидкости при очень низкой температуре, вблизи абсолютного нуля. Как следует из классической физики, при такой температуре атомы должны прекратить свое движение, образуя тем самым кристалл. Однако, в силу квантовых эффектов некоторые вещества с небольшой атомной массой и с высокой нулевой энергией (минимальная энергия системы) способны оставаться жидкостями.
Волны де Бройля – один из параметров, возникающий из математических глубин квантовой механики, который определяет плотность вероятности нахождения частицы в выбранном объеме конфигурационного пространства (пространство всех возможных значений всех параметров частицы). Чтобы заметить проявление квантовых эффектов в жидкости, требуется, чтобы длина волны де Бройля, вычисленная по энергии теплового движения частиц, была близка к значению расстояния между этими частицами. К примеру, для гелия подобное отношение будет возникать при температуре всего 2-3 К.

Зависимость состояния гелия от давления (ось ординат) и температуры (ось абсцисс)
Как уже говорилось ранее, вещества с высокой нулевой энергией способны становиться квантовыми жидкостями при низких температурах. Высокая нулевая энергия подразумевает наличие колебаний частиц даже при сверхнизких температурах. Если же амплитуда этих колебаний близка к среднему расстоянию между частицами вещества, то оно сохранит свою жидкую форму.
В зависимости от частиц, составляющих жидкость, она может быть бозонной (состоять из бозонов) и фермионной (состоять из фермионов).
Сверхтекучесть и другие свойства
Бозонные квантовые жидкости способны протекать через узкие капилляры или щели без какого-либо трения, это свойство называется сверхтекучестью. Примечательно, что подобное явление наблюдается не только у квантовых жидкостей, но и в некоторых бозе-конденсатах и даже в твердом гелии.
Материалы по теме

Сверхтекучесть объясняется следующим образом. Как известно, из квантовой механики следует, что бозоны способны находиться в одном состоянии. Тогда при низкой температуре, когда скорость частиц относительно невысокая, бозонам более энергетически выгодно сливаться в одно состояние, нежели взаимодействовать со стенками сосуда, то есть переходить в иное состояние, при котором возникает трение.
Сверхтекучесть была экспериментально достигнута жидкостями таких веществ как гелий-II (2,172 К), гелий-3, гелий-4 и водород (0,15 К). Вероятнее всего в недрах нейтронных звезд вещество находится в сверхтекучем состоянии.
В отличие от бозе-жидкостей, обладающих сверхтекучестью, фермионные квантовые жидкости с понижением температуры все менее способны пропускать звук, который, как известно, передается посредством колебаний частиц.
Частицы, составляющие сверхтекучие жидкости обычно представляются в виде конденсата Бозе — Эйнштейна.
comments powered by HyperComments
Понравилась запись? Расскажи о ней друзьям!
Просмотров записи: 627

spacegid.com
Сверхтекучая жидкость Википедия
 Аномальное течение гелия-II
Аномальное течение гелия-II Сверхтеку́честь — способность вещества в особом состоянии (квантовой жидкости), возникающем при температурах, близких к абсолютному нулю (термодинамическая фаза), протекать через узкие щели и капилляры без трения. До недавнего времени сверхтекучесть была известна только у жидкого гелия, однако в последние годы[когда?] сверхтекучесть была обнаружена и в других системах: в разреженных атомных бозе-конденсатах, твёрдом гелии.
Сверхтекучесть объясняется следующим образом. Поскольку атомы гелия являются бозонами, квантовая механика допускает нахождение в одном состоянии произвольного числа частиц. Вблизи абсолютного нуля температур все атомы гелия оказываются в основном энергетическом состоянии. Поскольку энергия состояний дискретна, атом может получить не любую энергию, а только такую, которая равна энергетическому зазору между соседними уровнями энергии. Но при низкой температуре энергия столкновений может оказаться меньше этой величины, в результате чего рассеяние энергии попросту не будет происходить. Жидкость будет течь без трения.
История открытия
 Почтовая марка России 2000 года
Почтовая марка России 2000 года Сверхтекучесть жидкого гелия-II ниже лямбда-точки (T = 2,172 К) была экспериментально открыта в 1938 году П. Л. Капицей (Нобелевская премия по физике за 1978 год). Уже до этого было известно, что при прохождении этой точки жидкий гелий испытывает фазовый переход, переходя из полностью «нормального» состояния (называемого гелий-I) в новое состояние так называемого гелия-II, однако только Капица показал, что гелий-II течёт вообще (в пределах экспериментальных погрешностей) без трения.
Теория явления сверхтекучего гелия-II была разработана Л. Д. Ландау (Нобелевская премия по физике за 1962 год).
Основные факты
На сегодняшний день установлено, что коэффициент вязкости у гелия-II меньше 10−12 Па·с, в то время как у гелия-I вблизи температуры 4,22 К этот коэффициент имеет величину порядка 10−6 Па·с.
Двухжидкостная модель гелия-II
 Рис.1 Относительная доля нормальной компоненты в гелии-II
Рис.1 Относительная доля нормальной компоненты в гелии-II В рамках двухжидкостной модели (также известной как «двухкомпонентная модель»), гелий-II представляет собой смесь двух взаимопроникающих жидкостей: сверхтекучей и нормальной компонент. Сверхтекучая компонента представляет собой собственно жидкий гелий, находящийся в квантово-коррелированном состоянии, в некоторой степени аналогичном состоянию бозе-конденсата (однако, в отличие от конденсата атомов разреженного газа, взаимодействие между атомами гелия в жидкости достаточно сильно, поэтому теория бозе-конденсата неприменима впрямую к жидкому гелию). Эта компонента движется без трения, обладает нулевой температурой и не участвует в переносе энергии в форме теплоты. Нормальная компонента представляет собой газ квазичастиц двух типов: фононов и ротонов, то есть элементарных возбуждений квантовокоррелированной жидкости; она движется с трением и участвует в переносе энергии.
При нулевой температуре в гелии отсутствует свободная энергия, которую можно было бы потратить на рождение квазичастиц, и поэтому гелий находится полностью в сверхтекучем состоянии. При повышении температуры плотность газа квазичастиц (прежде всего, фононов) растёт, и доля сверхтекучей компоненты падает. Вблизи температуры лямбда-точки концентрация квазичастиц становится столь велика, что они образуют уже не газ, а жидкость квазичастиц, и наконец при превышении температуры лямбда-точки макроскопическая квантовая когерентность теряется, и сверхтекучая компонента пропадает вовсе. Относительная доля нормальной компоненты показана на Рис. 1.
При протекании гелия сквозь щели с малой скоростью, сверхтекучая компонента, по определению, обтекает все препятствия без потери кинетической энергии, то есть без трения. Трение могло бы возникнуть, если бы какой-либо выступ щели порождал квазичастицы, уносящие в разные стороны импульс жидкости. Однако такое явление при малых скоростях течения энергетически невыгодно, и только при превышении критической скорости течения начинают генерироваться ротоны.
Эта модель, во-первых, хорошо объясняет разнообразные термомеханические, светомеханические и другие явления, наблюдающиеся в гелии-II, а во-вторых, прочно базируется на квантовой механике.
Сверхтекучесть в иных системах
- Построена сверхтекучая модель атомного ядра, которая достаточно хорошо описывает экспериментальные данные[1].
- В 1995 году в экспериментах с разреженными газами щелочных металлов были достигнуты достаточно низкие температуры для того, чтобы газ перешел в состояние бозе-эйнштейновского конденсата. Как и ожидалось на основании теоретических вычислений, полученный конденсат вёл себя как сверхтекучая жидкость. В последующих экспериментах было установлено, что при движении тел сквозь этот конденсат со скоростями меньше критической никакой передачи энергии от тела к конденсату не происходит.
- В 2000 году Ян Петер Тоэнниэс демонстрирует сверхтекучесть водорода при 0,15 K[2]
- В 2004 году было объявлено об открытии сверхтекучести и у твёрдого гелия. Последующие исследования, однако, показали, что ситуация далеко не столь проста, и потому говорить об экспериментальном обнаружении этого явления пока преждевременно.
- С 2004 года, на основании результатов ряда теоретических работ[3] предполагается, что при давлениях порядка 4 миллионов атмосфер и выше водород становится не способным переходить в твердую фазу при любом охлаждении (как и гелий при нормальном давлении) образуя тем самым сверхтекучую жидкость. Прямые экспериментальные подтверждения или опровержения пока отсутствуют.
- Существуют также работы, предсказывающие сверхтекучесть в холодном нейтронном или кварковом агрегатном состоянии. Это может оказаться важным для понимания физики нейтронных и кварковых звёзд.
- В 2005 году была открыта сверхтекучесть в холодном разреженном газе фермионов[4].
- В 2009 году была продемонстрирована сверхтекучесть типа «supersolid» в холодном разреженном газе рубидия[5].
Современные направления исследования
- Турбулентность в сверхтекучей жидкости
- Сверхтекучесть в системах с внутренними степенями свободы
- Связь сверхпроводящих и сверхтекучих фаз
- Спиновая сверхтекучесть
- Поиск новых веществ со сверхтекучими фазами
Высокотемпературная сверхтекучесть
Высокотемпературная сверхтекучесть — термин, относящийся к явлениям, напоминающим обычную «низкотемпературную» сверхтекучесть, проявляющимся при комнатных температурах. Физика этого явления также отличается от физики обычной сверхтекучести. Например, течение воды в трубе круглого сечения обладает свойствами высокотемпературной сверхтекучести. Это проявляется в том, что значение числа Рейнольдса, при котором происходит переход к турбулентному режиму, превосходит на два порядка значения для труб другого сечения, что можно истолковать как понижение на столько же порядков эффективной вязкости. Это можно объяснить, если — так же, как и в теории обычной сверхтекучести — представить жидкость (воду) как состоящую из двух компонент — нормальной и сверхтекучей. Плотность сверхтекучей компоненты примерно на два порядка превышает плотность нормальной компоненты, что и объясняет увеличение на столько же значение критического числа Рейнольдса, которое зависит от плотности нормальной компоненты.
Физика этого явления связана с учетом взаимодействия волн плотности в жидкости и упругих волн изгиба в стенках трубы. За счет этой связи происходит ослабление отталкивания одноимённых флуктуаций плотности жидкости благодаря экранированию его указанным взаимодействием. Условие экранирования совпадает с условием Ландау обычной сверхтекучести. Спектр возбуждений в рассматриваемой системе имеет при малых волновых числах фононный характер, а при звуковых скоростях течения обладает также характерным ротонным минимумом, напоминая спектр возбуждений в сверхтекучем гелии.[источник не указан 97 дней]
Явление высокотемпературной сверхтекучести может иметь место при движении морских животных (дельфинов) в воде, позволяя им развивать большую скорость. Первоначальные оценки необходимых для этого мышечных усилий при условии турбулентного обтекания показали, что эти усилия превышают возможности дельфинов в 10 раз (парадокс Грея). Впоследствии выяснилось, что благодаря строению кожи дельфина турбулентность гасится благодаря демпфирующему влиянию кожи и обтекающий поток ламинаризуется. Высказывалось мнение, что демпфирование — активный процесс, регулируемый центральной нервной системой дельфина.[источник не указан 97 дней]
Это явление использовалось на практике (М. Крамер, Германия, 1938 г.) для разработки специального покрытия торпед (ламинофоло), позволившего без увеличения мощности двигателя увеличить их скорость в 1,5 — 2 раза. В России в 1920-х годах изобретатель П. В. Митурич предложил конструкцию судна, у которого движителем выступал гибкий корпус, совершающий волнообразные движения.[источник не указан 97 дней]
Практическое использование. Современная практика
Практическое использование. Будущие перспективы использования
Примечания
См. также
Ссылки
- Ландау Л. Д., Лифшиц Е. М. Гидродинамика. — М.: Наука, 1986, 736 с.
- Зайко Ю. Н. Распространение волн в жидкости, протекающей в жидкости с упругими стенками // Письма в ЖТФ, 2001, т. 27, вып. 16, с. 27—31.
- Зайко Ю. Н. Модель течения жидкости в сосуде с упругими стенками // Письма в ЖТФ, 2002, т. 28, вып. 24, с. 15—19.
- P. W. Carpenter, C. Davis, A. D. Lucey. Hydrodynamics and compliant walls: Does dolphin have a secret? //Current Science, 25 September 2000, Vol. 70, No 6, pp. 758—765.
- Шапиро Л. С. Создание и развитие подводного корабля. К патентам Природы
- О роли нулевых колебаний в образовании сверхпроводящего и сверхтекучего состояний
Обзорные статьи
Литература
- Кресин В. З. Сверхпроводимость и сверхтекучесть. — М.: Наука, 1978. — 187 с.
- Бондарев Б. В. Метод матриц плотности в квантовой теории сверхтекучести. — М.: Спутник, 2014. — 91 с.
- Тилли Д. Р., Тилли Дж. Свехтекучесть и сверхпроводимость. — М.: Мир, 1977. — 304 с.
wikiredia.ru
|
|
Сверхтекучесть жидкого гелияВ 1937 году Петр Леонидович Капица обнаружил у гелия парадоксальное свойство: при охлаждении до температур, близких к абсолютному нулю, жидкий гелий не только не становится твердым, но теряет вязкость, переходя в состояние сверхтекучести. Абсолютный нуль - температура, при которой хаотическое движение атомов прекращается. Следовательно, при абсолютном нуле все тела должны быть твердыми. Жидкий гелий - единственное вещество, которое не затвердевает при абсолютном нуле. Вот как излагал сам Ландау сущность сверхтекучести в публичной лекции (стенограмма лекции приводится в некотором сокращении): "Наиболее замечательное свойство жидкого гелия было открыто советским физиком Петром Леонидовичем Капицей. Капица показал, что жидкий гелий вовсе лишен всякой вязкости. Что такое вязкость" Это способность жидкости сопротивляться движению. Вы ясно представляете себе, насколько труднее было бы плавать в меде, чем в воде. Соответственно этому говорят, что мед " это жидкость, гораздо более вязкая, чем вода. Жидкости по своей вязкости бывают самые различные " от очень слабо вязких жидкостей, как вода, спирт, до очень вязких жидкостей типа глицерипа, меда и даже стекла, которое тоже является необычайно вязкой жидкостью, и т. д. Жидкий гелий I обладает малой вязкостью по сравнению с другими жидкостями. Но эта вязкость еще вполне нормальна и измерима. Она в 500 раз меньше вязкости воды. Петр Леонидович Капица произвел очень простой и необычайно важный эксперимент. Он наблюдал протекание гелия через очень тонкие щели. Щели эти были настолько тонкие, что даже такая с обычной точки зрения невязкая жидкость, как вода, вытекала бы через эти щели в течение многих п многих суток. Оказалось, что жидкий гелий II протекает через щели в течение нескольких секунд. Петру Леонидовичу Капице удалось показать, что вязкость гелия отличается от вязкости воды не менее чем в миллиард раз. Это только верхний предел, связанный с точностью экспериментов, тот предел вязкости, который наблюдал Петр Леонидович Капица. Вязкость гелия II оказалась столь маленькой, что вообще не могла быть измерена. Можно утверждать, что жидкий гелий II просто лишен всякой вязкости. Это явление получило название сверхтекучести. Поэтому гелий II называют сверхтекучей жидкостью. Открытие Петром Леонидовичем Капицей сверхтекучести сразу объяснило казавшееся почти мистичетским перетекание гелия из одного сосуда в другой. Все жидкости, смачивающие стенки, покрывают эти стенки очень тонким слоем. Этот тонкий слой незаметен для глаза и обычно вообще никак не проявляется. В жидком гелии благодаря сверхтекучести жидкость довольно быстро перетекает из сосуда по этой тонкой пленке, которая имеет толщину стотысячной доли миллиметра. Таким образом, одно из явлений, казавшихся мистическим, получило свое объяснение. Зато, однако, открылись многие другие явления, оказавшиеся еще более непонятными. Прежде всего оказалось, что когда гелий течет через щель, то происходит странное явление с теплом. Если гелий протекает из одного сосуда в другой через очень тонкую щель, то оказывается, что при этом гелий в том сосуде, куда он вытекает, охлаждается, а в том сосуде, из которого он вытекает, нагревается. Это явление получило название термомеханического эффекта и само по себе представлялось крайне удивительным. Еще более удивительным представляется другое свойство гелия. Капица показал, что гелий сверхтекуч, то есть мгновенно вытекает через всякую щель. Протекание через щель есть не единственный способ измерения вязкости. В физике известны и другие способы, которые основаны на сопротивлении жидкости движению в ней тела. Если вы хотите измерить вязкость воды, вы можете измерить ее двумя способами: вы можете пропускать воду через щель и можете двигать в воде тело и определять вязкость по тем силам, которые действуют на это тело. Для гелия были применены оба эти способа, и оказалось, что в то время, когда у всех жидкостей они приводят к совершенно тождественным не только качественным, по и количественным результатам, у гелия они приводят, если можно так выразиться, к результатам противоположным. Жидкий гелий II при протекании через щель сверхтекуч, то есть не обнаруживает вовсе никакой вязкости. Он обнаруживает сопротивление движению тела, то есть в то время, когда все обыкновенные жидкости обладают обыкновенной вязкостью, жидкий гелий обладает двумя совершенно различными по природе вязкостями: одной - бесконечно малой, отсутствующей, и другой - вполне качественной, измеримой вязкостью. Капице удалось сделать эксперименты, кажущиеся еще более удивительными. Эксперимент заключается в следующем. В большой сосуд с гелием была погружена бульбочка с идущей от нее трубочкой, открытой и наполненной гелием. В этой бульбочке гелий слегка подогревался. Что произошло бы с какой-нибудь жидкостью? Жидкость нагревалась бы, тепло выходило бы в окружающую жидкость, и можно было бы обнаружить, что разные места жидкости обладают разной температурой. Петр Леонидович Капица поместил напротив отверстия капилляра легкое крылышко и, двигая этим крылышком, показал, что из отверстия капилляра бьет струя гелия. Обстоятельство, удивительное во всех отношениях. Удивителен не столько сам факт, что при нагревании ни с того ни с сего бьет струя гелия. Еще более удивительным является то обстоятельство, что сосуд при этом не пустеет. Если из сосуда систематически вырывается струя жидкости, то через короткое время в сосуде не должно ничего остаться. В данном случае никаких изменений не происходит. Сосуд остается наполненным гелием, как вначале. Получается "библейский эксперимент" в стиле куста, который горит и не сгорает. Так и здесь: бульбочка, из которой бьет струя и которая при этом не пустеет, а остается столь же полной, какой была и вначале. Это обстоятельство является одним из многочисленных примеров (некоторые из которых я уже упомянул) парадоксальности свойств жидкого гелия. Его свойства на первый взгляд кажутся совершенно нелепыми, как в известном анекдоте о жирафе, про которого сказано, что "такого не может быть". Такое примерно ощущение вызывают свойства жидкого гелия. Получается ощущение, что вообще такого не может быть. Само собою разумеется, что никаких логических противоречий здесь, как и в других областях физики, быть не может. Это показывает только на то, что причины этих свойств лежат в очень необычных вещах, очень чуждых нашему представлению. И действительно, в дальнейшем мне удалось построить теорию, которая объяснила некоторые существенные свойства жидкого гелия. Было бы невозможно даже в самых общих чертах попытаться объяснить вам сущность этой теории. Она основана на одном из величайших достижений физики двадцатого века, так называемой квантовой механике, Квантовая механика - это бесконечно сложная как методически, так и по заложенным в ней физическим понятиям область теории физики. Она характеризуется тем, что многие из используемых ею понятий очень плохо доступны нашему восприятию. <...> Оказывается, что чисто теоретически квантовая механика наделила жидкость, находящуюся при низких температурах, близких к абсолютному нулю, при которых находится жидкий гелий, следующей особенностью. Для того чтобы объяснить эту особенность, я напомню очень старую историю о некоторой теории, которая в свое время фигурировала в физике. В свое время в физике фигурировала такая, разумеется никогда не существовавшая, жидкость, как теплород. Считалось, что наряду с обыкновенной жидкостью существует еще тепловая жидкость и что если тело является теплым, то это значит, что в нем больше теплорода. Если же меньше теплорода, значит, оно соответственно становится более холодным. Теплород - жидкость, специально придуманная для объяснения этих явлений. Эксперименты доказали, что никакой тепловой жидкости не существует, а тепло есть движение частиц жидкости. Оказывается, что в гелии сохранилось кое-что от теплорода, кое-что, конечно, в очень своеобразном смысле. Именно в обыкновенной жидкости тепло непосредственно связано со всей жидкостью, точнее говоря, со всей массой жидкости. Иначе обстоит дело в жидком гелии. Там оказывается, что тепло связано не со всей массой жидкости, а только с ее частью, причем меньшей частью, то есть если говорить как бы о тепловой жидкости, то в обыкновенных жидкостях тепловая жидкость - это вся жидкость, в жидком же гелии тепловая жидкость - это часть жидкости. Чем меньшая часть, тем ниже температура. Эта часть получила название нормальной массы гелия. <...> При температуре 2,19 градуса Кельвина происходит переход от гелия II к гелию I. Выше этой температуры вся масса гелия - это нормальная масса. Ниже этой температуры - часть гелия, которая пе связана с теплом. И чем ниже температура, тем меньшая часть гелия связана с теплом. При абсолютном нуле весь гелий никак с теплом не связан. Из существования таких двух масс гелия - массы нормальной и остальной массы, которая получила название массы сверхтекучести, следует другое, не менее на первый взгляд чудовищное утверждение, что гелий способен одновременно к двум движениям. Имея две массы, хотя в одном и том же месте, в одном и том же объеме, гелий может совершать одновременно два различных движения одновременно в одной точке жидкости. В то время как обычная жидкость в одной точке имеет одну определенную скорость, гелий в одной точке имеет две скорости, совершенно различные. Одна из скоростей называется скоростью нормального движения, другая - скоростью сверхтекучего движения. Теория показывает, что оба эти движения должны обладать существенно различными свойствами. Нормальное движение, связанное с теплом, является нормальным во всех смыслах. Именпо оно обладает всеми свойствами всякого нормального движения, в частности оно связано с вязкостью. Наоборот, сверхтекучее движение не связано с теплом, не связано ни с какой вязкостью. На первый взгляд такая концепция имеет характер почти абсурда. Может показаться, что это довольно бессмысленное рассуждение, которое если и объясняет что-нибудь, то чисто словесным образом, без всякого реального результата. Однако <...> это не так. Теория не только объяснила те явления, о которых я говорил, но и предсказала ряд явлений, которые в дальнейшем были обнаружены экспериментами. Больше того, те два движения, о которых я вам сказал и существование которых производит такое дикое впечатление, может быть непосредственно наблюдено на экспериментах. Это может быть сделано следующим образом. Представьте себе, что цилиндрический сосуд с гелием начинает вращаться, причем вращаться очень медленно, настолько медленно, что жидкость должна увлекаться при своем движении стенками сосуда. Так как жидкий гелий способен к двум движениям и его масса состоит из двух масс, то увлекаться будет только одна из них, именно нормальная масса гелия. Сверхтекучее движение, не будучи связано пи с какой вязкостью, не будет ни в каком взаимодействии со стенками сосуда и увлекаться не будет. При вращении гелия будет вращаться часть гелия, между тем как при вращении любой другой жидкости будет вращаться вся жидкость. Эти замечательные результаты были обнаружены докторантом Элевтером Андроникашвили , который непосредственно проделал, я бы не сказал, эти, но аналогичные опыты, отличающиеся от изложенного опыта только деталями. При этом эксперименте оказалось, что выше 2,19 градуса гелий увлекается весь, ниже этой температуры гелий увлекается тем меньшим коичеством, чем ниже температура. Таким образом, Андроникашвили имел возможность непосредственно измерить, какая часть массы гелия является нормальной и какая часть массы гелия является сверхтекучей. Сверхтекучее движение не есть теоретическая функция, а это есть вообще реально наблюдающееся при эксперименте явление. Количественно полученные результаты тоже оказались в прекрасном согласии с теорией. Таким образом, эксперимент Андроникашвили наглядно показал, что заложенная в теории жидкого гелия основа, несмотря на свою странность, отвечает реальной действительности. Легко также видеть, что с помощью этих теоретических представлений действительно объясняются те кажущиеся противоречивыми явления, которые наблюдаются в жидком гелии. Возьмем этот удивительный эксперимент Капицы с вытекающей струей жидкого гелия. С точки зрения теории сверхтекучести ясно, в чем тут дело. Нагревание жидкого гелия происходит необычным образом. Обычным образом тепло переходит от молекулы к молекуле, без всего движения в целом. В жидком гелии под влиянием нагревания возникают одновременно два движения: тепло скапливается слева, потом движется слева направо вместе с нормальным движением. Сверхтекучее же движение, наоборот, движется в противоположную сторону, так что полное количество гелия в бульбочке, естественно, установилось неизменно. В жидком гелии, в котором распространяется тепло, имеется два встречных потока: поток нормальный и поток сверхтекучий, движущийся в противоположную сторону. Сверхтекучий поток благодаря отсутствию вязкости никак не действует на погруженные в пего предметы. Нормальный поток вследствие вязкости действует па погруженные предметы. Поэтому крылышко, погруженное в гелий, чувствуя струю вытекающего гелия, колеблется, по оно совершенно не чувствует струи втекающего гелия. Этим же обстоятельством объясняется и грандиозная теплопроводность гелия - способность к передаче громадного количества тепла. В обыкновеннной жидкости, где тепло передается молекулярным движением - от молекулы к молекуле, тепло передается медленно. В жидком гелии тепло буквально течет слева направо. Таким образом может быть передано огромное количество тепла. Наличием обоих течений объясняется и другое парадоксальное обстоятельство, о котором я говорил, именно то, что гелий обладает одновременно двумя вязкостями, в зависимости от того, каким способом эти вязкости измеряются. Когда гелий вытекает через щель, то, естественно, происходит сверхтекучее течение, не связанное с какой-либо вязкостью. Поэтому никакой вязкости мы при этом не наблюдаем. Наоборот, когда в гелии движется тело, то это тело, естественно, взаимодействует не только со сверхтекучей, но и с нормальной частью, откуда и наблюдается вязкость. Этим объясняется и другое обстоятельство, а именно знаменитый гелиево-термический эффект - то, что гелий охлаждается в том сосуде, куда втекает через тонкие щели, и нагревается в том сосуде, откуда вытекает. При сверхтекучем движении гелий вытекает без всякого тепла. В том сосуде, куда он втекает, одно и то же количество тепла, а гелия становится больше. Соответственно гелий в этом сосуде охлаждается. Наоборот, в том сосуде, откуда гелий вытекал, гелия становилось меньше, а тепла оставалось столько же. Естественно, что гелий нагревался. Естественно, что все основные явления, которые наблюдаются в гелии, находят себе теоретическое объяснение. Кроме этих явлений теорией было предсказано еще одно явление, также в дальнейшем открытое в эксперименте. Именно в жидком гелии, в отличие от обыкновенной жидкости, могут распространяться два разных звука. Звук - это колебание плотности жидкости. В вязкой жидкости могут происходить такие колебания, которые распространяются с определенной скоростью. Такие колебания могут распространяться в гелии I со скоростью 150 метров в секунду. С такой же скоростью звук может распространяться в гелии II. Теория показала, что наряду с таким звуком в гелии может распространяться звук особого рода, связанный с возможностью двух движений. В гелии возможен еще один звук, когда в целом масса не перемещается, а колебание нормальной и сверхтекучей части происходит друг относительно друга. Содержащая тепло часть гелия колеблется относительно остального гелия. Этот звук получил название второго звука и был открыт Пешковым , который обнаружил распространение этого звука в гелии II. Распространение второго звука легко отличить от распространения обыкновенного звука, потому что его скорость не имеет ничего общего со скоростью обыкновенного звука: вместо 250 метров в секунду составляет 20 метров в секунду. Пешкову удалось обнаружить, что в гелии действительно распространяется особого вида звук. Он вызывается колебанием тепла. Если производить колебания температуры в обыкновенной жидкости, эти колебания быстро затухают. Никакого второго звука здесь не получается. Если колебать температуру в жидком гелии, то это колебание распространяется как звук с определенной скоростью, которая составляет около 20 метров в секунду. Таким образом, и это явление, предсказанное теоретически, было наблюдено при эксперименте. Есть, разумеется, и много других явлений, более или менее удивительных, происходящих с жидким гелием. Разумеется, не следует думать, что все явления, происходящие в жидком гелии, Замечание Читателя Труевцев Петр Николаевич [email protected] Прекрасная статья, только речь в ней шла о нейтронном газе в составе электромагнитной волны,то есть химического элемента гелия.Сверхтекучесть нейтронного газа - это первая ласточка о жидкости, как агрегатного состояния нейтронного газа. Ссылки:1. Квантовая жидкость2. Ландау - теория сверхтекучести жидкого гелия3. Ландау: Ленинская и Нобелевская премии 1962 г.4. Рецензия С. Шноля на книги "Двадцатый век Анны Капицы"5. Капица Петр Леонидович (1894-1984)
|
Сверхтекучесть - это... Что такое Сверхтекучесть?

 Аномальное течение Гелия-II
Аномальное течение Гелия-II Сверхтеку́честь — способность вещества в особом состоянии (квантовой жидкости), возникающем при понижении температуры к абсолютному нулю (термодинамическая фаза), протекать через узкие щели и капилляры без трения. До недавнего времени сверхтекучесть была известна только у жидкого гелия, однако в последние годы сверхтекучесть была обнаружена и в других системах: в разреженных атомных бозе-конденсатах, твёрдом гелии.
Сверхтекучесть объясняется следующим образом. Поскольку атомы гелия являются бозонами, квантовая механика допускает нахождение в одном состоянии произвольного числа частиц. Вблизи абсолютного нуля температур все атомы гелия оказываются в основном энергетическом состоянии. Поскольку энергия состояний дискретна, атом может получить не любую энергию, а только такую, которая равна энергетическому зазору между соседними уровнями энергии. Но при низкой температуре энергия столкновений может оказаться меньше этой величины, в результате чего рассеяния энергии попросту не будет происходить.
Жидкость будет течь без трения.История открытия

 Почтовая марка России 2000 года
Почтовая марка России 2000 года Сверхтекучесть жидкого гелия-II ниже лямбда-точки (T = 2,172 К) была экспериментально открыта в 1938 году П. Л. Капицей (Нобелевская премия по физике за 1978 год). Уже до этого было известно, что при прохождении этой точки жидкий гелий испытывает фазовый переход, переходя из полностью «нормального» состояния (называемого гелий-I) в новое состояние так называемого гелия-II, однако только Капица показал, что гелий-II течёт вообще (в пределах экспериментальных погрешностей) без трения.
Теория явления сверхтекучего гелия-II была разработана Л. Д. Ландау (Нобелевская премия по физике за 1962 год).
Основные факты
На сегодняшний день установлено, что коэффициент вязкости у гелия-II меньше 10−12 Па·с, в то время как у гелия-I вблизи температуры 4,22 К этот коэффициент имеет величину порядка 10−6 Па·с.
Двухжидкостная модель гелия-II

 Рис.1 Относительная доля нормальной компоненты в гелии-II
Рис.1 Относительная доля нормальной компоненты в гелии-II В рамках двухжидкостной модели, гелий-II представляет собой смесь двух взаимопроникающих жидкостей: сверхтекучей и нормальной компонент. Сверхтекучая компонента представляет собой собственно жидкий гелий, находящийся в квантово-коррелированном состоянии, аналогичном состоянию бозе-конденсата (однако, в отличие от конденсата разреженных паров атомов, гелий находится в режиме сильной связи). Эта компонента движется без трения, обладает нулевой температурой и не участвует в переносе энергии в форме теплоты. Нормальная компонента представляет собой газ квазичастиц двух типов: фононов и ротонов, то есть элементарных возбуждений квантовокоррелированной жидкости; она движется с трением и участвует в переносе энергии.
При нулевой температуре в гелии отсутствует свободная энергия, которую можно было бы потратить на рождение квазичастиц, и поэтому гелий находится полностью в сверхтекучем состоянии. При повышении температуры плотность газа квазичастиц (прежде всего, фононов) растёт, и доля сверхтекучей компоненты падает. Вблизи температуры лямбда-точки концентрация квазичастиц становится столь велика, что они образуют уже не газ, а жидкость квазичастиц, и наконец при превышении температуры лямбда-точки макроскопическая квантовая когерентность теряется, и сверхтекучая компонента пропадает вовсе. Относительная доля нормальной компоненты показана на Рис.1.
При протекании гелия сквозь щели с малой скоростью, сверхтекучая компонента, по определению, обтекает все препятствия без потери кинетической энергии, то есть без трения. Трение могло бы возникнуть, если бы какой-либо выступ щели порождал бы квазичастицы, уносящие в разные стороны импульс жидкости. Однако такое явление при малых скоростях течения энергетически невыгодно, и только при превышении критической скорости течения начинают генерироваться ротоны.
Эта модель, во-первых, хорошо объясняет разнообразные термомеханические, светомеханические и т. п. явления, наблюдающиеся в гелии-II, а во-вторых, прочно базируется на квантовой механике.
Сверхтекучесть в иных системах
- В 1995 году в экспериментах с разреженными газами щелочных металлов были достигнуты достаточно низкие температуры для того, чтобы газ перешел в состояние бозе-эйнштейновского конденсата. Как и ожидалось на основании теоретических вычислений, полученный конденсат вёл себя как сверхтекучая жидкость. В последующих экспериментах было установлено, что при движении тел сквозь этот конденсат со скоростями меньше критической никакой передачи энергии от тела к конденсату не происходит.
- В 2000 году Ян Петер Тоэнниэс демонстрирует сверхтекучесть водорода при 0,15 K[1]
- В 2004 году было объявлено об открытии сверхтекучести и у твёрдого гелия. Последующие исследования, однако, показали, что ситуация далеко не столь проста, и потому говорить об экспериментальном обнаружении этого явления пока преждевременно.
- С 2004 года, на основании результатов ряда теоретических работ[2] предполагается, что при давлениях порядка 4 миллионов атмосфер и выше водород становится не способным переходить в твердую фазу при любом охлаждении (как и гелий при нормальном давлении) образуя тем самым сверхтекучую жидкость. Прямые экспериментальные подтверждения или опровержения пока отсутствуют.
- Существуют также работы, предсказывающие сверхтекучесть в холодном нейтронном или кварковом агрегатном состоянии. Это может оказаться важным для понимания физики нейтронных и кварковых звёзд.
- В 2005 году была открыта сверхтекучесть в холодном разреженном газе фермионов[3].
- В 2009 году была продемонстрирована сверхтекучесть типа «supersolid» в холодном разреженном газе рубидия[4].
Современные направления исследования
- Турбулентность в сверхтекучей жидкости
- Сверхтекучесть в системах с внутренними степенями свободы
- Связь сверхпроводящих и сверхтекучих фаз
- Спиновая сверхтекучесть
- Поиск новых веществ со сверхтекучими фазами
Высокотемпературная сверхтекучесть
Высокотемпературная сверхтекучесть-термин, относящийся к явлениям, напоминающим обычную «низкотемпературную» сверхтекучесть, проявляющимся при комнатных температурах. Физика этого явления также отличается от физики обычной сверхтекучести. Например, течение воды в трубе круглого сечения обладает свойствами высокотемпературной сверхтекучести. Это проявляется в том, что значение числа Рейнольдса, при котором происходит переход к турбулентному режиму превосходит на два порядка значения для труб другого сечения, что можно истолковать как понижение на столько же порядков эффективной вязкости. Это можно объяснить, если так же как и в теории обычной сверхтекучести представить жидкость (воду) как состоящую из двух компонент-нормальной и сверхтекучей. Плотность сверхтекучей компоненты примерно на два порядка превышает плотность нормальной компоненты, что и объясняет увеличение на столько же значение критического числа Рейнольдса, которое зависит от плотности нормальной компоненты. Физика этого явления связана с учетом взаимодействия волн плотности в жидкости и упругих волн изгиба в стенках трубы. За счет этой связи происходит ослабление отталкивания одноименных флуктуаций плотности жидкости благодаря экранированию его указанным взаимодействием. Условие экранирования совпадает с условием Ландау обычной сверхтекучести. Спектр возбуждений в рассматриваемой системе имеет при малых волновых числах фононный характер, а при звуковых скоростях течения обладает также характерным ротонным минимумом, напоминая спектр возбуждений в сверхтекучем гелии.
Явление высокотемпературной сверхтекучести может иметь место при движении морских животных (дельфинов) в воде, позволяя им развивать большую скорость. Первоначальные оценки необходимых для этого мышечных усилий при условии турбулентного обтекания показали, что эти усилия превышают возможности дельфинов в 10 раз (парадокс Грея). Впоследствии выяснилось, что благодаря строению кожи дельфина турбулентность гасится благодаря демпфирующему влиянию кожи и обтекающий поток ламинаризуется. Высказывалось мнение, что демпфирование — активный процесс, регулируемый центральной нервной системой дельфина.
Это явление использовалось на практике (М. Крамер, Германия, 1938 г.) для разработки специального покрытия торпед (ламинофоло), позволившего без увеличения мощности двигателя увеличить их скорость в 1,5 — 2 раза. В России, в 20-е годы 20-го в., изобретатель П. В. Митурич предложил конструкцию судна, у которого движителем выступал гибкий корпус, совершающий волнообразные движения.
Практическое использование. Современная практика
Практическое использование. Будущие перспективы использования
Примечания
См. также
Ссылки
- Ландау Л. Д., Лифшиц Е. М. Гидродинамика. М.: Наука, 1986, 736 с.
- Зайко Ю. Н. Распространение волн в жидкости, протекающей в жидкости с упругими стенками. Письма в ЖТФ, 2001, Т. 27, вып. 16, с. 27-31.
- Зайко Ю. Н. Модель течения жидкости в сосуде с упругими стенками. Письма в ЖТФ, 2002, Т. 28, вып. 24, с. 15-19.
- P.W. Carpenter, C. Davis, A.D. Lucey. Hydrodynamics and compliant walls: Does dolphin have a secret?./Current Science, 25 September 2000, Vol. 70, No 6, pp. 758—765.
- Л. С. Шапиро. Создание и развитие подводного корабля. К патентам Природы
- О роли нулевых колебаний в образовании сверхпроводящего и сверхтекучего состояний
Обзорные статьи
dic.academic.ru
Сверхтекучесть
Сверхтеку́честь — способность вещества в особом состоянии (квантовой жидкости), возникающем при понижении температуры к абсолютному нулю (термодинамическая фаза), протекать через узкие щели и капилляры без трения. До недавнего времени сверхтекучесть была известна только у жидкого гелия, однако в последние годы сверхтекучесть была обнаружена и в других системах: в разреженных атомных бозе-конденсатах, твёрдом гелии.Сверхтекучесть объясняется следующим образом. Поскольку атомы гелия являются бозонами, квантовая механика допускает нахождение в одном состоянии произвольного числа частиц. Вблизи абсолютного нуля температур все атомы гелия оказываются в основном энергетическом состоянии. Поскольку энергия состояний дискретна, атом может получить не любую энергию, а только такую, которая равна энергетическому зазору между соседними уровнями энергии. Но при низкой температуре энергия столкновений может оказаться меньше этой величины, в результате чего рассеяние энергии попросту не будет происходить. Жидкость будет течь без трения.
Содержание
- 1 История открытия
- 2 Основные факты
- 3 Двухжидкостная модель гелия-II
- 4 Сверхтекучесть в иных системах
- 5 Современные направления исследования
- 6 Высокотемпературная сверхтекучесть
- 7 Практическое использование. Современная практика
- 8 Практическое использование. Будущие перспективы использования
- 9 Примечания
- 10 См. также
- 11 Ссылки
- 11.1 Обзорные статьи
- 12 Литература
История открытия
Почтовая марка России 2000 годаСверхтекучесть жидкого гелия-II ниже лямбда-точки (T = 2,172 К) была экспериментально открыта в 1938 году П. Л. Капицей (Нобелевская премия по физике за 1978 год). Уже до этого было известно, что при прохождении этой точки жидкий гелий испытывает фазовый переход, переходя из полностью «нормального» состояния (называемого гелий-I) в новое состояние так называемого гелия-II, однако только Капица показал, что гелий-II течёт вообще (в пределах экспериментальных погрешностей) без трения.
Теория явления сверхтекучего гелия-II была разработана Л. Д. Ландау (Нобелевская премия по физике за 1962 год).
Основные факты
На сегодняшний день установлено, что коэффициент вязкости у гелия-II меньше 10−12 Па·с, в то время как у гелия-I вблизи температуры 4,22 К этот коэффициент имеет величину порядка 10−6 Па·с.
Двухжидкостная модель гелия-II
Рис.1 Относительная доля нормальной компоненты в гелии-IIВ рамках двухжидкостной модели (также известной как «двухкомпонентная модель»), гелий-II представляет собой смесь двух взаимопроникающих жидкостей: сверхтекучей и нормальной компонент. Сверхтекучая компонента представляет собой собственно жидкий гелий, находящийся в квантово-коррелированном состоянии, в некоторой степени аналогичном состоянию бозе-конденсата (однако, в отличие от конденсата атомов разреженного газа, взаимодействие между атомами гелия в жидкости достаточно сильно, поэтому теория бозе-конденсата неприменима впрямую к жидкому гелию). Эта компонента движется без трения, обладает нулевой температурой и не участвует в переносе энергии в форме теплоты. Нормальная компонента представляет собой газ квазичастиц двух типов: фононов и ротонов, то есть элементарных возбуждений квантовокоррелированной жидкости; она движется с трением и участвует в переносе энергии.
При нулевой температуре в гелии отсутствует свободная энергия, которую можно было бы потратить на рождение квазичастиц, и поэтому гелий находится полностью в сверхтекучем состоянии. При повышении температуры плотность газа квазичастиц (прежде всего, фононов) растёт, и доля сверхтекучей компоненты падает. Вблизи температуры лямбда-точки концентрация квазичастиц становится столь велика, что они образуют уже не газ, а жидкость квазичастиц, и наконец при превышении температуры лямбда-точки макроскопическая квантовая когерентность теряется, и сверхтекучая компонента пропадает вовсе. Относительная доля нормальной компоненты показана на Рис. 1.
При протекании гелия сквозь щели с малой скоростью, сверхтекучая компонента, по определению, обтекает все препятствия без потери кинетической энергии, то есть без трения. Трение могло бы возникнуть, если бы какой-либо выступ щели порождал бы квазичастицы, уносящие в разные стороны импульс жидкости. Однако такое явление при малых скоростях течения энергетически невыгодно, и только при превышении критической скорости течения начинают генерироваться ротоны.
Эта модель, во-первых, хорошо объясняет разнообразные термомеханические, светомеханические и другие явления, наблюдающиеся в гелии-II, а во-вторых, прочно базируется на квантовой механике.
Сверхтекучесть в иных системах
- Построена сверхтекучая модель атомного ядра, которая достаточно хорошо описывает экспериментальные данные.
- В 1995 году в экспериментах с разреженными газами щелочных металлов были достигнуты достаточно низкие температуры для того, чтобы газ перешел в состояние бозе-эйнштейновского конденсата. Как и ожидалось на основании теоретических вычислений, полученный конденсат вёл себя как сверхтекучая жидкость. В последующих экспериментах было установлено, что при движении тел сквозь этот конденсат со скоростями меньше критической никакой передачи энергии от тела к конденсату не происходит.
- В 2000 году Ян Петер Тоэнниэс демонстрирует сверхтекучесть водорода при 0,15 K
- В 2004 году было объявлено об открытии сверхтекучести и у твёрдого гелия. Последующие исследования, однако, показали, что ситуация далеко не столь проста, и потому говорить об экспериментальном обнаружении этого явления пока преждевременно.
- С 2004 года, на основании результатов ряда теоретических работ предполагается, что при давлениях порядка 4 миллионов атмосфер и выше водород становится не способным переходить в твердую фазу при любом охлаждении (как и гелий при нормальном давлении) образуя тем самым сверхтекучую жидкость. Прямые экспериментальные подтверждения или опровержения пока отсутствуют.
- Существуют также работы, предсказывающие сверхтекучесть в холодном нейтронном или кварковом агрегатном состоянии. Это может оказаться важным для понимания физики нейтронных и кварковых звёзд.
- В 2005 году была открыта сверхтекучесть в холодном разреженном газе фермионов.
- В 2009 году была продемонстрирована сверхтекучесть типа «supersolid» в холодном разреженном газе рубидия.
Современные направления исследования
- Турбулентность в сверхтекучей жидкости
- Сверхтекучесть в системах с внутренними степенями свободы
- Связь сверхпроводящих и сверхтекучих фаз
- Спиновая сверхтекучесть
- Поиск новых веществ со сверхтекучими фазами
Высокотемпературная сверхтекучесть
Высокотемпературная сверхтекучесть — термин, относящийся к явлениям, напоминающим обычную «низкотемпературную» сверхтекучесть, проявляющимся при комнатных температурах. Физика этого явления также отличается от физики обычной сверхтекучести. Например, течение воды в трубе круглого сечения обладает свойствами высокотемпературной сверхтекучести. Это проявляется в том, что значение числа Рейнольдса, при котором происходит переход к турбулентному режиму превосходит на два порядка значения для труб другого сечения, что можно истолковать как понижение на столько же порядков эффективной вязкости. Это можно объяснить, если так же как и в теории обычной сверхтекучести представить жидкость (воду) как состоящую из двух компонент-нормальной и сверхтекучей. Плотность сверхтекучей компоненты примерно на два порядка превышает плотность нормальной компоненты, что и объясняет увеличение на столько же значение критического числа Рейнольдса, которое зависит от плотности нормальной компоненты. Физика этого явления связана с учетом взаимодействия волн плотности в жидкости и упругих волн изгиба в стенках трубы. За счет этой связи происходит ослабление отталкивания одноименных флуктуаций плотности жидкости благодаря экранированию его указанным взаимодействием. Условие экранирования совпадает с условием Ландау обычной сверхтекучести. Спектр возбуждений в рассматриваемой системе имеет при малых волновых числах фононный характер, а при звуковых скоростях течения обладает также характерным ротонным минимумом, напоминая спектр возбуждений в сверхтекучем гелии.
Явление высокотемпературной сверхтекучести может иметь место при движении морских животных (дельфинов) в воде, позволяя им развивать большую скорость. Первоначальные оценки необходимых для этого мышечных усилий при условии турбулентного обтекания показали, что эти усилия превышают возможности дельфинов в 10 раз (парадокс Грея). Впоследствии выяснилось, что благодаря строению кожи дельфина турбулентность гасится благодаря демпфирующему влиянию кожи и обтекающий поток ламинаризуется. Высказывалось мнение, что демпфирование — активный процесс, регулируемый центральной нервной системой дельфина.
Это явление использовалось на практике (М. Крамер, Германия, 1938 г.) для разработки специального покрытия торпед (ламинофоло), позволившего без увеличения мощности двигателя увеличить их скорость в 1,5 — 2 раза. В России, в 20-е годы XX века, изобретатель П. В. Митурич предложил конструкцию судна, у которого движителем выступал гибкий корпус, совершающий волнообразные движения.
Практическое использование. Современная практика
Практическое использование. Будущие перспективы использования
Примечания
- ↑ Сверхпроводимость и сверхтекучесть, 1978, с. 127
- ↑ Evidence for Superfluidity in Para-Hydrogen Clusters Inside Helium-4 Droplets at 0.15 Kelvin (англ.)
- ↑ Egor Babaev; Asle Sudbo, N. W. Ashcroft. A superconductor to superfluid phase transition in liquid metallic hydrogen (англ.) (18 Oct 2004). Проверено 20 марта 2009.
- ↑ Сверхтекучесть в холодном разреженном газе фермионов
- ↑ Сверхтекучесть типа «supersolid» в холодном разреженном газе рубидия
См. также
- Критерий сверхтекучести Ландау
Ссылки
- Ландау Л. Д., Лифшиц Е. М. Гидродинамика. М.: Наука, 1986, 736 с.
- Зайко Ю. Н. Распространение волн в жидкости, протекающей в жидкости с упругими стенками. Письма в ЖТФ, 2001, Т. 27, вып. 16, с. 27-31.
- Зайко Ю. Н. Модель течения жидкости в сосуде с упругими стенками. Письма в ЖТФ, 2002, Т. 28, вып. 24, с. 15-19.
- P.W. Carpenter, C. Davis, A.D. Lucey. Hydrodynamics and compliant walls: Does dolphin have a secret?./Current Science, 25 September 2000, Vol. 70, No 6, pp. 758—765.
- Л. С. Шапиро. Создание и развитие подводного корабля. К патентам Природы
- О роли нулевых колебаний в образовании сверхпроводящего и сверхтекучего состояний
Обзорные статьи
- Гинзбург В. Л. — Сверхтекучесть и сверхпроводимость во Вселенной (Успехи Физических Наук — УФН Т.97 1969, № 4) PDF
- Дмитриев В. В. Спиновая сверхтекучесть в 3He, УФН, т.175 (2005), N.1, 85-92
Литература
- Кресин В. З. Сверхпроводимость и сверхтекучесть. — М.: Наука, 1978. — 187 с.
- Бондарев Б.В. Метод матриц плотности в квантовой теории сверхтекучести. — М.: Спутник, 2014. — 91 с.
- Тилли Д. Р., Тилли Дж. Свехтекучесть и сверхпроводимость. — М.: Мир, 1977. — 304 с.
| Аморфные тела (Стеклообразное состояние) • Кристаллы (Монокристалл • Поликристалл • Кристаллит) • Сверхтекучее твёрдое тело |
| Расплав • Перегретая • Переохлаждённая • Сверхкритическая жидкость • Квантовая жидкость (Сверхтекучесть) • Жидкий кристалл |
| Вырожденный газ • Пар |
| Электромагнитная • Кварк-глюонная • Глазма |
| Гели (Аэрогель) • Растворы • Коллоидные системы • Грубодисперсная • Свободнодисперсная коллоидная • Дым • Золь • Суспензия • Эмульсия |
| Термодинамическая фаза • Плавление • Кристаллизация • Сублимация • Десублимация • Кипение • Испарение • Парообразование • Конденсация • Критическая точка |
| Нормальные и стандартные условия • Статистика Ферми — Дирака • Уравнение состояния |
Сверхтекучесть Информация о
СверхтекучестьСверхтекучестьСверхтекучесть Информация Видео
Сверхтекучесть Просмотр темы.Сверхтекучесть что, Сверхтекучесть кто, Сверхтекучесть объяснение
There are excerpts from wikipedia on this article and video
www.turkaramamotoru.com